模拟题2016.11.14

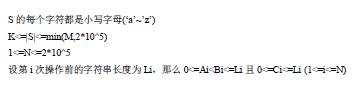
Pictrue Not Found Picture Not Found

这一道题的正解是倒推（然后有难度吗？）,直接用results[i]表示第i位在某次操作完成后的位置（第几次呢，就看外重循环吧）接着可以分成三种情况

当results[j] <= ins_i时，对位置没有影响
当results[j] > ins_i && results[j] <= ins_i + end_i - begin_i时，正好被copy走了，所以位置是begin_i + results_i - ins_i
以上两种都不是，那就是被copy插进来的部分导致往后移了end_i - begin_i位，所以减去就好了

Code

#include<iostream>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef bool boolean;
#define INF 0xfffffff
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
template<typename T>
inline void readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-');
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
}

inline void getLine(char* str){
    int i = 0;
    while((str[i] = getchar()) != '\n' && ~str[i])    i++;
    str[i] = 0;
}

int k, m;
int n;
char s[200005];
int *from;
int *end;
int *ins;

inline void init(){
    readInteger(k);
    readInteger(m);
    getchar();
    getLine(s + 1);
    readInteger(n);
    from = new int[(const int)(n + 1)];
    end = new int[(const int)(n + 1)];
    ins = new int[(const int)(n + 1)];
    for(int i = 1; i <= n; i++){
        readInteger(from[i]);
        readInteger(end[i]);
        readInteger(ins[i]);
    }
}

int *results;

inline void solve(){
    results = new int[(const int)(k + 1)];
    for(int i = 1; i <= k; i++)
        results[i] = i;
    for(int i = n; i >= 1; i--){
        for(int j = 1; j <= k; j++){
            int& x = results[j];
            if(x <= ins[i])    continue;    //没有影响
            else if(x <= ins[i] + (end[i] - from[i])){
                x = from[i] + x - ins[i];
            }else{
                x -= end[i] - from[i];
            }
        }
    }
    for(int i = 1; i <= k; i++)
        putchar(s[results[i]]);
}

int main(){
    freopen("A.in", "r", stdin);
    freopen("A.out", "w", stdout);
    init();
    solve();
    return 0;
}

Picture Not Found

这道题是一道水题，首先可以这么想，对于每个s_i的前4^{i - 1}都是可以通过计算得到了，那我们弄三个前缀和，统计J、O、I分别出现的次数，接着递归调用去计算就好了。如果到了最后一位，不用管，什么都可以。最后找一个最大值，然后就可以ac了。

Code

#include<iostream>
#include<cstdio>
#include<cctype>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<fstream>
#include<sstream>
#include<algorithm>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
using namespace std;
typedef bool boolean;
#define INF 0xfffffff
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
template<typename T>
inline void readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-');
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
}

int power[11];
inline void getPower(){
    power[0] = 1;
    for(int i = 1; i <= 10; i++)
        power[i] = power[i - 1] * 4;
}

const char ch[3] = {'J', 'O', 'I'};
int n;
char* str;

inline void init(){
    readInteger(n);
    str = new char[power[n] + 1];
    getchar();
    for(int i = 1; i <= power[n]; i++)
        str[i] = getchar();
}

int *sj;
int *so;
int *si;
inline void presum(){
    sj[0] = so[0] = si[0] = 0;
    for(int i = 1; i <= power[n]; i++){
        sj[i] = sj[i - 1], so[i] = so[i - 1], si[i] = si[i - 1];
        if(str[i] == 'J')    sj[i]++;
        else if(str[i] == 'O')    so[i]++;
        else if(str[i] == 'I')    si[i]++; 
    }
    for(int i = 1; i <= power[n]; i++){
        int j = power[n] + i;
        sj[j] = sj[j - 1], so[j] = so[j - 1], si[j] = si[j - 1];
        if(str[i] == 'J')    sj[j]++;
        else if(str[i] == 'O')    so[j]++;
        else if(str[i] == 'I')    si[j]++; 
    }
}

int *replaces;

inline void solve2(int n, int b){
    if(n == 0)    return;    
    int seg = power[n - 1];
    for(int i = 1; i <= power[::n]; i++){
        replaces[i] += (seg - (sj[i + b + seg - 1] - sj[i + b - 1])) +
                        (seg - (so[i + b +seg * 2 - 1] - so[i + b + seg - 1])) +
                        (seg - (si[i + b + seg * 3 - 1] - si[i + b + seg * 2 - 1])); 
    }
    solve2(n - 1, b + seg * 3);
}

int main(){
    freopen("B.in", "r", stdin);
    freopen("B.out", "w", stdout);
    getPower();
    init();
    sj = new int[(const int)(2 * power[n] + 1)];
    so = new int[(const int)(2 * power[n] + 1)];
    si = new int[(const int)(2 * power[n] + 1)];
    presum();
    replaces = new int[(const int)(power[n] + 1)];
    memset(replaces, 0, sizeof(int) * (power[n] + 1));
    solve2(n, 0);
    int minv = power[n];
    for(int i = 1; i <= power[n]; i++)
        smin(minv, replaces[i]);
    printf("%d", minv);
    return 0;
}

Picture Not Found

    这道题算是今天最有价值的一道题，废话不多说，讲解法
    如果不知道如何dp的可以看看这个帖子合唱队形,dp的话就不用管那个不拔，但是却不产生作用的，只管像这样做，只把i和j中比j高的拔掉就行了。于是得到了dp方程:
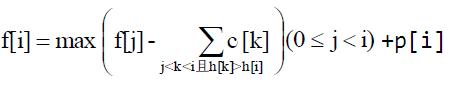
Picture Not Found
    中间那一串求和其实可以先预处理出来，但是时间复杂度是O(n²)，还是过不去，这时可以考虑用数据结构维护。首先要按照高度来查询对不对，又要区间更新(拔掉这一棵)，还要单点修改，然后还要区间求最值，是不是可以想到线段树这个好东西。但是内存上过不去对不对？如果按照n的大小来建树内存的开销就很小了。那么可以吧h进行离散化。每次查询就查询1 ~ h_i的最值。接着将高度小于等于它的部分全部减去c_i。然后单点更新h_i的最值。
Notice:

第二次dp的时候不要重建树,不然会TLE
lazy标记和数据都要使用long long
注意延时更新的地方不要手抖把+=写成=了

Code

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cctype>
  4 #include<cstring>
  5 #include<cstdlib>
  6 #include<cmath>
  7 #include<fstream>
  8 #include<sstream>
  9 #include<algorithm>
 10 #include<map>
 11 #include<set>
 12 #include<queue>
 13 #include<vector>
 14 #include<stack>
 15 using namespace std;
 16 typedef bool boolean;
 17 #define INF 0xfffffff
 18 #define smin(a, b) a = min(a, b)
 19 #define smax(a, b) a = max(a, b)
 20 template<typename T>
 21 inline void readInteger(T& u){
 22     char x;
 23     int aFlag = 1;
 24     while(!isdigit((x = getchar())) && x != '-');
 25     if(x == '-'){
 26         x = getchar();
 27         aFlag = -1;
 28     }
 29     for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
 30     ungetc(x, stdin);
 31     u *= aFlag;
 32 }
 33 
 34 template<typename T>
 35 inline void putInteger(T u){
 36     if(u == '0'){
 37         putchar('0');
 38         return;
 39     }
 40     if(u < 0){
 41         putchar('-');
 42         u *= -1;
 43     }
 44     stack<char>    s;
 45     while(u != 0)    s.push(u % 10 + '0'), u /= 10;
 46     while(!s.empty())    putchar(s.top()), s.pop();
 47 }
 48 
 49 const long long inf = (1ll << 60);
 50 
 51 template<typename T>
 52 class TreeNode{
 53     public:
 54         int from;
 55         int end;
 56         TreeNode* left;
 57         TreeNode* right;
 58         T data;
 59         T lazy;
 60         TreeNode(int from, int end, T data):from(from), end(end), left(NULL), right(NULL), data(data), lazy(0){    }
 61 };
 62 
 63 template<typename T>
 64 class SegTree{
 65     public:
 66         TreeNode<T>* root;
 67         SegTree():root(NULL){}
 68         SegTree(int size){
 69             build(root, 1, size);
 70         }
 71         inline void pushUp(TreeNode<T>* node){
 72             node->data = max(node->left->data, node->right->data);
 73         }
 74         inline void pushDown(TreeNode<T>* node){
 75             if(node->left != NULL){
 76                 node->left->lazy += node->lazy;
 77                 node->left->data -= node->lazy;
 78                 node->right->lazy += node->lazy;
 79                 node->right->data -= node->lazy; 
 80             }
 81             node->lazy = 0;
 82         }
 83         void build(TreeNode<T>*& node, int from, int end){
 84             if(from == end){
 85                 node = new TreeNode<T>(from, end, 0);
 86                 return;
 87             }
 88             node = new TreeNode<T>(from, end, 0);
 89             int mid = (from + end) >> 1;
 90             build(node->left, from, mid);
 91             build(node->right, mid + 1, end);
 92         }
 93         void update(TreeNode<T>* node, int from, int end, long long val){
 94             if(from == node->from && end == node->end){
 95                 node->lazy += val;
 96                 node->data -= val;
 97                 return;
 98             }
 99             if(node->lazy != 0)    pushDown(node); 
100             int mid = (node->from + node->end) >> 1;
101             if(from > mid)    update(node->right, from, end, val);
102             else if(end <= mid)    update(node->left, from, end, val);
103             else{
104                 update(node->left, from, mid, val);
105                 update(node->right, mid + 1, end, val);
106             }
107         }
108         void update(TreeNode<T>* node, int d, long long val){
109             if(node->from == d && node->end == d){
110                 smax(node->data, val);
111                 return;
112             }
113             if(node->lazy != 0)    pushDown(node);
114             int mid = (node->from + node->end) >> 1;
115             if(d > mid)    update(node->right, d, val);
116             else update(node->left, d, val);
117             pushUp(node);
118         }
119         long long query(TreeNode<T>* node, int from, int end){
120             if(from == node->from && end == node->end){
121                 return node->data;
122             }
123             if(node->lazy != 0)    pushDown(node);
124             int mid = (node->from + node->end) >> 1;
125             if(from > mid)    return query(node->right, from, end);
126             else if(end <= mid)    return query(node->left, from, end);
127             else{
128                 return max(query(node->left, from, mid), query(node->right, mid + 1, end));
129             }
130         }
131         void clean(TreeNode<T>* node){
132             if(node == NULL)    return;
133             clean(node->left);
134             clean(node->right);
135             node->data = 0;
136             node->lazy = 0;
137         }
138 };
139 
140 int n;
141 int *h, *p, *c;
142 
143 inline void init(){
144     readInteger(n);
145     h = new int[(const int)(n + 1)];
146     p = new int[(const int)(n + 1)];
147     c = new int[(const int)(n + 1)];
148     for(int i = 1; i <= n; i++){
149         readInteger(h[i]);
150         readInteger(p[i]);
151         readInteger(c[i]);
152     }
153 }
154 
155 typedef class Data{
156     public:
157         int height;
158         int index;
159         Data(const int height = 0, const int index = 0):height(height), index(index){    }
160         boolean operator <(Data another) const {
161             return this->height < another.height;
162         }
163 }Data;
164 
165 int ch;
166 Data* data;
167 inline void discretization(){
168     data = new Data[(const int)(n + 1)];
169     data[0] = Data(0, 0);
170     for(int i = 1; i <= n; i++)
171         data[i] = Data(h[i], i);
172     sort(data + 1, data + n + 1);
173     for(int i = 1; i <= n; i++){
174         h[data[i].index] = (data[i].height == data[i - 1].height) ? (ch) : (++ch);
175     }
176 }
177 
178 long long *lf, *rf;
179 SegTree<long long> st;
180 inline void solve(){
181     lf = new long long[(const int)(n + 1)];
182     rf = new long long[(const int)(n + 2)];
183     lf[0] = rf[n + 1] = 0;
184     st = SegTree<long long>(ch);
185     for(int i = 1; i <= n; i++){
186         lf[i] = st.query(st.root, 1, h[i]) + p[i];
187         st.update(st.root, 1, h[i], c[i]);
188         st.update(st.root, h[i], lf[i]);
189     }
190     st.clean(st.root);
191     for(int i = n; i >= 1; i--){
192         rf[i] = st.query(st.root, 1, h[i]) + p[i];
193         st.update(st.root, 1, h[i], c[i]);
194         st.update(st.root, h[i], rf[i]);
195     }
196     long long result = 0;
197     for(int i = 1; i <= n; i++)
198         smax(result, lf[i] + rf[i] - p[i]);
199     putInteger(result);
200 }
201 
202 int main(){
203     freopen("C.in", "r", stdin);
204     freopen("C.out", "w", stdout);
205     init();
206     discretization();
207     solve();
208     return 0;
209 }

posted @ 2016-11-14 20:19 阿波罗2003 阅读(154) 评论(0) 编辑收藏举报

刷新页面返回顶部

模拟题2016.11.14

Code

Code

Code

公告