noip2007部分题
1.统计数字
题目描述 Description
某次科研调查时得到了n个自然数，每个数均不超过1500000000（1.5*109）。已知不相同的数
不超过10000 个，现在需要统计这些自然数各自出现的次数，并按照自然数从小到大的顺序输出统
计结果。
输入描述 Input Description
第1行是整数n，表示自然数的个数。
第2~n+1 行每行一个自然数。
输出描述 Output Description
输出包含m行（m为n个自然数中不相同数的个数），按照自然数从小到大
的顺序输出。每行输出两个整数，分别是自然数和该数出现的次数，其间用一个空格隔开。
样例输入 Sample Input
8
2
4
2
4
5
100
2
100
样例输出 Sample Output
2 3
4 2
5 1
100 2
数据范围及提示 Data Size & Hint
【限制】
40%的数据满足：1<=n<=1000
80%的数据满足：1<=n<=50000
100%的数据满足：1<=n<=200000，每个数均不超过1 500 000 000（1.5*10^9）
（来自http://codevs.cn/problem/1164/）
这道题没有什么特别的技术含量，排个序，再统计就行了
1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<cctype> 5 #include<map> 6 #include<set> 7 using namespace std; 8 template<typename T> 9 inline void readInteger(T& u){ 10 char x; 11 while(!isdigit((x = getchar()))); 12 for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0'); 13 ungetc(x, stdin); 14 } 15 int n; 16 int* list; 17 int main(){ 18 freopen("count.in", "r", stdin); 19 freopen("count.out", "w", stdout); 20 readInteger(n); 21 list = new int[(const int)(n + 1)]; 22 for(int i = 0; i < n; i++){ 23 readInteger(list[i]); 24 } 25 sort(list, list + n); 26 int counter = 1; 27 int last = list[0]; 28 for(int i = 1; i < n; i++){ 29 if(list[i] != last){ 30 cout<<last<<" "<<counter<<endl; 31 last = list[i]; 32 counter = 1; 33 }else counter++; 34 } 35 cout<<last<<" "<<counter<<endl; 36 return 0; 37 }
2.矩阵取数游戏
题目描述 Description
【问题描述】
帅帅经常跟同学玩一个矩阵取数游戏：对于一个给定的n*m 的矩阵，矩阵中的每个元素aij均
为非负整数。游戏规则如下：
1. 每次取数时须从每行各取走一个元素，共n个。m次后取完矩阵所有元素；
2. 每次取走的各个元素只能是该元素所在行的行首或行尾；
3. 每次取数都有一个得分值，为每行取数的得分之和，每行取数的得分= 被取走的元素值*2i，
其中i 表示第i 次取数（从1 开始编号）；
4. 游戏结束总得分为m次取数得分之和。
帅帅想请你帮忙写一个程序，对于任意矩阵，可以求出取数后的最大得分。
输入描述 Input Description
第1行为两个用空格隔开的整数n和m。
第2~n+1 行为n*m矩阵，其中每行有m个用单个空格隔开的非负整数。
输出描述 Output Description
输出 仅包含1 行，为一个整数，即输入矩阵取数后的最大得分。
样例输入 Sample Input
2 3
1 2 3
3 4 2
样例输出 Sample Output
82
数据范围及提示 Data Size & Hint
样例解释
第 1 次：第1 行取行首元素，第2 行取行尾元素，本次得分为1*21+2*21=6
第2 次：两行均取行首元素，本次得分为2*22+3*22=20
第3 次：得分为3*23+4*23=56。总得分为6+20+56=82
【限制】
60%的数据满足：1<=n, m<=30, 答案不超过1016
100%的数据满足：1<=n, m<=80, 0<=aij<=1000
这道题首先一看数据范围就知道要用高精度，最好用上万进制以免其他地方处理不当导致TLE，
接着可以发现每一行取出来的得分和其他行没有关系，就可以分开计算，最后把所有行加起来就行了。
至于这个计算，很容易想到dp，用f[i][j]表示第i次取数，左边取了j个，或者f[i][j]表示左边取了i个，
右边取了j个，总之能表示出左右分别取了多少个就行了。
就说第一种的方程
f[i][j] = max(f[i - 1][j - 1] + a[l][j], f[i - 1][j] + a[l][m - i + j - 1]);
我做的时候稍微有点不一样，但是思路还是一样的，仍然很容易理解
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cctype> 5 #include<map> 6 using namespace std; 7 typedef bool boolean; 8 template<typename T> 9 inline void readInteger(T& u){ 10 char x; 11 while(!isdigit((x = getchar()))); 12 for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0'); 13 ungetc(x, stdin); 14 } 15 typedef class HP{ 16 public: 17 int w[10]; 18 HP(){ 19 memset(w, 0, sizeof(w)); 20 } 21 HP(long long x){ 22 memset(w, 0, sizeof(w)); 23 if(x == 0) w[0] = 1; 24 while(x > 0){ 25 w[++w[0]] = x % 10000; 26 x /= 10000; 27 } 28 } 29 HP operator *(int x){ 30 HP result; 31 result[0] = w[0] + 1; 32 for(int i = 1; i <= w[0] + 1; i++){ 33 result[i] += w[i] * x; 34 result[i + 1] += result[i] / 10000; 35 result[i] %= 10000; 36 } 37 while(result[result[0]] == 0 && result[0] > 1) result[0]--; 38 return result; 39 } 40 HP operator +(HP another){ 41 HP result; 42 result[0] = max(w[0], another[0]) + 1; 43 for(int i = 1; i < result[0]; i++){ 44 result[i] += w[i] + another[i]; 45 result[i + 1] += result[i] / 10000; 46 result[i] %= 10000; 47 } 48 while(result[result[0]] == 0 && result[0] > 1) result[0]--; 49 return result; 50 } 51 boolean operator <(HP another) const{ 52 if(w[0] != another[0]) return w[0] < another[0]; 53 for(int i = w[0]; i >= 1; i--){ 54 if(w[i] != another[i]) return w[i] < another[i]; 55 } 56 return false; 57 } 58 int& operator [](int pos){ 59 return w[pos]; 60 } 61 }HP; 62 int matrix[85][85]; 63 HP result[85]; 64 HP pow_2[85]; 65 int n, m; 66 HP f[85][85][2]; 67 inline void solve(int lines){ 68 memset(f, 0, sizeof(f)); 69 f[1][0][1] = pow_2[1] * matrix[lines][1]; 70 f[1][0][0] = pow_2[1] * matrix[lines][m]; 71 for(int i = 2; i <= m; i++){ 72 for(int j = 0; j < i; j++){ 73 HP temp = max(f[i - 1][j][0], f[i - 1][j - 1][1]); 74 f[i][j][1] = temp + pow_2[i] * matrix[lines][j + 1]; 75 f[i][j][0] = temp + pow_2[i] * matrix[lines][m - i + j + 1]; 76 } 77 } 78 for(int i = 0; i < m; i++){ 79 for(int j = 0; j < 3; j++){ 80 result[lines] = max(result[lines], f[m][i][j]); 81 } 82 } 83 } 84 ostream& operator <<(ostream& out, HP& x){ 85 int buf[6]; 86 for(int i = x[0]; i >= 1; i--){ 87 if(i != x[0]){ 88 memset(buf, 0, sizeof(buf)); 89 int c = x[i]; 90 while(c > 0){ 91 buf[++buf[0]] = c % 10; 92 c /= 10; 93 } 94 for(int i = 4; i >= 1; i--) 95 putchar(buf[i] + '0'); 96 }else{ 97 printf("%d",x[i]); 98 } 99 } 100 return out; 101 } 102 inline void init(){ 103 readInteger(n); 104 readInteger(m); 105 for(int i = 1; i <= n; i++){ 106 for(int j = 1, x; j <= m; j++){ 107 readInteger(matrix[i][j]); 108 } 109 } 110 pow_2[1] = HP(2); 111 for(int i = 2; i <= m + 1; i++) 112 pow_2[i] = pow_2[i - 1] * 2; 113 } 114 HP ans; 115 int main(){ 116 freopen("game.in", "r", stdin); 117 freopen("game.out", "w", stdout); 118 init(); 119 ans[0] = 1; 120 for(int i = 1; i <= n; i++){ 121 solve(i); 122 ans = ans + result[i]; 123 } 124 cout<<ans; 125 return 0; 126 }
3.树网的核
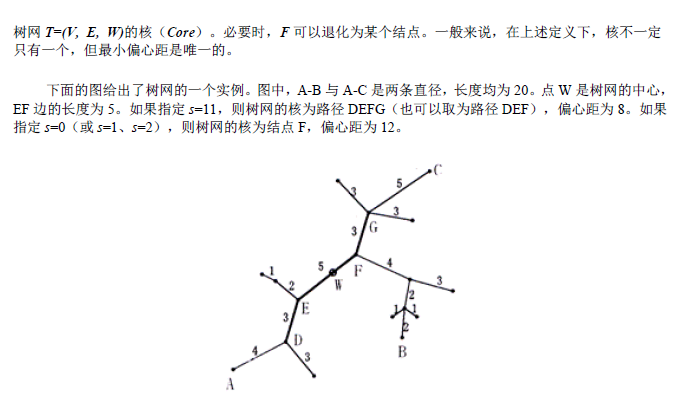
思考一下，是不是并没有想出dp之类的十分高效的算法？再看看数据范围，n最大才300，不怕，暴力都很容易过（当然，
这是对于现在的电脑）。不过有一点还是要清楚，一定得找出一条直径来，接着在上面一段一段地去枚举。
需要枚举所有的直径吗？不需要，画画图就知道了
接着还有，怎么提高枚举的效率？首先选一段的偏心距不会多于选一个节点作为核的偏心距，而且这一道题也不要求输出
方案，所以能选多少就选多少，避免很多排列。
求直径还不清楚的话，我就再说一下，首先随便从一个点开始dfs找出一个离它最远的点，再从这个点开始dfs找出一个离它
最远的点，然后这两个点的距离就是直径的长度，注意还要记录路径
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cctype> 5 #include<vector> 6 using namespace std; 7 typedef bool boolean; 8 template<typename T> 9 inline void readInteger(T& u){ 10 char x; 11 while(!isdigit((x = getchar()))); 12 for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0'); 13 ungetc(x, stdin); 14 } 15 typedef class Edge{ 16 public: 17 int end; 18 int next; 19 int v; 20 Edge(const int end = 0, const int next = 0, const int v = 0):end(end),next(next), v(v){} 21 }Edge; 22 int ce; 23 int *h; 24 Edge* edge; 25 inline void addEdge(int from, int end, int v){ 26 edge[++ce] = Edge(end, h[from], v); 27 h[from] = ce; 28 } 29 int* buf; 30 int imn; 31 int maxdis; 32 int *rd; 33 int *brd; 34 boolean *visable; 35 void dfs(int* path, int node, int dis, int last, int d){ 36 if(path != NULL){ 37 buf[++buf[0]] = node; 38 if(buf[0] != 1) 39 brd[buf[0] - 1] = d; 40 } 41 if(dis > maxdis){ 42 maxdis = dis; 43 if(path != NULL){ 44 memcpy(path, buf, sizeof(int) * (buf[0] + 1)); 45 memcpy(rd, brd, sizeof(int) * (buf[0] + 1)); 46 } 47 imn = node; 48 } 49 for(int i = h[node]; i != 0; i = edge[i].next){ 50 int e = edge[i].end; 51 if(e == last) continue; 52 if(!visable[e]) continue; 53 dfs(path, e, dis + edge[i].v, node, edge[i].v); 54 } 55 if(path != NULL) buf[0]--; 56 } 57 int n, s; 58 int *road; 59 inline void init(){ 60 readInteger(n); 61 readInteger(s); 62 edge = new Edge[(const int)(n * 2)]; 63 h = new int[(const int)(n + 1)]; 64 buf = new int[(const int)(n + 1)]; 65 road = new int[(const int)(n + 1)]; 66 rd = new int[(const int)(n + 1)]; 67 brd = new int[(const int)(n + 1)]; 68 memset(h, 0, sizeof(int) * (n + 1)); 69 memset(buf, 0, sizeof(int) * (n + 1)); 70 visable = new boolean[(const int)(n + 1)]; 71 memset(visable, true, sizeof(boolean) * (n + 1)); 72 for(int i = 1, a, b, v; i < n; i++){ 73 readInteger(a); 74 readInteger(b); 75 readInteger(v); 76 addEdge(a, b, v); 77 addEdge(b, a, v); 78 } 79 } 80 inline void solve(){ 81 dfs((int*)0, 1, 0, 0, 0); 82 maxdis = 0; 83 dfs(road, imn, 0, 0, 0); 84 buf[0] = 0; 85 maxdis = 0; 86 int len = 0; 87 int l = 1, r = 1; 88 int cn = 1; 89 int result = 0xfffffff; 90 visable[road[1]] = false; 91 while(r <= road[0] && l <= r){ 92 while(r < road[0] && (len + rd[r] <= s)){ 93 len += rd[r]; 94 r++; 95 cn++; 96 visable[road[r]] = false; 97 } 98 int p = 0; 99 for(int i = l; i <= r; i++){ 100 maxdis = 0; 101 dfs((int*)0, road[i], 0, 0, 0); 102 p = max(p, maxdis); 103 } 104 if(p < result) result = p; 105 visable[road[l]] = true; 106 cn--; 107 if(cn > 0) 108 len -= rd[l]; 109 else if(r < road[0]){ 110 len = 0; 111 r++; 112 visable[road[r]] = false; 113 } 114 l++; 115 } 116 cout<<result; 117 } 118 int main(){ 119 freopen("core.in", "r", stdin); 120 freopen("core.out", "w", stdout); 121 init(); 122 solve(); 123 return 0; 124 }
