NOIP Mayan游戏 - 搜索

Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个7行5列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见图6到图7）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见图1和图2)；

2、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1到图3）。

注意：
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图4，三个颜色为1的方块和三个颜色为2的方块会同时被消除，最后剩下一个颜色为2的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5所示的情形，5个方块会同时被消除）。

3、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1到图3给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0），将位于（3, 3）的方块向左移动之后，游戏界面从图1变成图2所示的状态，此时在一竖列上有连续三块颜色为4的方块，满足消除条件，消除连续3块颜色为4的方块后，上方的颜色为3的方块掉落，形成图3所示的局面。

格式

输入格式

第一行为一个正整数n，表示要求游戏关的步数。

接下来的5行，描述7*5的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个0 结束，自下向上表示每竖列方块的颜色编号（颜色不多于10种，从1开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式

如果有解决方案，输出n行，每行包含3个整数x，y，g，表示一次移动，每两个整数之间用一个空格隔开，其中（x，y）表示要移动的方块的坐标，g表示移动的方向，1表示向右移动，-1表示向左移动。注意：多组解时，按照x为第一关键字，y为第二关键字，1优先于-1，给出一组字典序最小的解。游戏界面左下角的坐标为(0, 0)。
如果没有解决方案，输出一行，包含一个整数-1。

样例1

样例输入1[复制]

 

3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0

样例输出1[复制]

 

2 1 1
3 1 1
3 0 1

限制

3s

提示

样例输入的游戏局面如图6到图11所示。依次移动的三步是：（2，1）处的方格向右移动，（3，1）处的方格向右移动，（3，0）处的方格向右移动，最后可以将棋盘上所有方块消除。

数据规模如下：
对于30%的数据，初始棋盘上的方块都在棋盘的最下面一行；
对于100%的数据，0 < n ≤ 5。

来源

NOIp2011提高组Day1第三题

(转自:https://vijos.org/p/1738)

---

　　题目意思应该还是很容易懂。首先是数据范围小，限时长，所以很可能是搜索。仔细想以后发现也不太可能是状压

dp之类的，就开始来思考搜索。

　　首先思考深搜还是广搜。因为一是字典序最小，而是保存的量比较大都至少是一个5 * 7的数组或是5个vector

所以深搜的速度会稍微快一些（广搜会把一层都搜完才会扩展）,内存开销也会小很多

　　接下来开始思考剪枝,有下面几种方案

　　1）因为是字典序最小，所以当左边有方块的时候从右向左移动不如从左向右移动（减去将近一半的节点）

　　2）源方块和目标方块颜色一样不需要移动，因为原来的图像看起来并没有改变

　　3）一种颜色剩余的数量大于0但是不足3个，返回

　　剪枝思考完毕了后，接下来是这个游戏特有的一些部分

　　1）下落，这个比较简单，就不多说了，看代码

　　2）消除，消除可以先标记，并不是直接消除，另外定一个5 * 7的数组，当某一位需要消除时将对应位上标为1

另外为了快捷可以3个单位地判断是否可以消除，另外在消除时还要加一个返回值判断是否消除了方块，因为消除完有

方块下落仍然会肯能产生消除，例如：

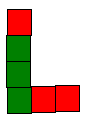
绿色消除后变成

最后红色的块也被消除

Code

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cctype>
#include<cstdlib>
#include<cmath>
using namespace std;
typedef bool boolean;
template<typename T>
inline void readInteger(T& u){
    char x;
    while(!isdigit((x = getchar())));
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
}
typedef class GameObject{
    public:
        int lines[5][7];
        int status[5];
        GameObject(){
            memset(lines, 0, sizeof(lines));
            memset(status, 0, sizeof(status));
        }
        void fallingDown(){
            for(int i = 0; i < 5; i++){
                int c = 0;
                for(int j = 0; j < 7; j++){
                    if(lines[i][j] != 0){
                        lines[i][c++] = lines[i][j];
                        if(c - 1 != j)
                            lines[i][j] = 0;
                    }
                }
                status[i] = c;
            }
        }
        boolean clean(){
            GameObject b;
            boolean aFlag = false;
            for(int i = 0; i < 5; i++){
                for(int j = 0; j < 5; j++){
                    if(lines[i][j] == lines[i][j + 1] && lines[i][j + 1] == lines[i][j + 2] &&
                        lines[i][j] != 0){
                        b[i][j] = b[i][j + 1] = b[i][j + 2] = -1;
                    }
                }
            }
            
            for(int i = 0; i < 7; i++){
                for(int j = 0; j < 3; j++){
                    if(lines[j][i] == lines[j + 1][i] && lines[j + 1][i] == lines[j + 2][i] &&
                        lines[j][i] != 0){
                        b[j][i] = b[j + 1][i] = b[j + 2][i] = -1;
                    }
                }
            }
            
            for(int i = 0; i < 5; i++){
                for(int j = 0; j < 7; j++){
                    if(b[i][j] < 0){
                        lines[i][j] = 0;
                        aFlag = true;
                    }
                }
            }
            return aFlag;
        }
        boolean move(int x, int y, int direc){
            if(x < 0 || x >= 5)        return false;
            if((x + direc) < 0 || (x + direc) >= 5)    return false;
            if(direc == -1 && lines[x - 1][y] != 0)    return false;
            if(lines[x][y] == lines[x + direc][y])    return false;
            swap(lines[x][y], lines[x + direc][y]);
            fallingDown();
            while(clean()) fallingDown();
            return true;        
        }
        int size(){
            int result = 0;
            for(int i = 0; i < 5; i++)
                result += status[i];
            return result;
        }
        int* operator [](int pos){
            return &lines[pos][0];
        }
}GameObject;
int n;
GameObject starter;
const int mover[2] = {1, -1};
inline void init(){
    readInteger(n);
    for(int i = 0, a; i < 5; i++){
        readInteger(a);
        while(a != 0){
            starter[i][starter.status[i]++] = a;
            readInteger(a);
        }
    }
}
int x[6];
int y[6];
int d[6];
void search(GameObject status, int depth){
    if(depth > n){
        if(status.size() > 0)    return;
        for(int i = 1; i <= n; i++){
            printf("%d %d %d\n", x[i], y[i], d[i]);
        }
        exit(0);
    }
    
    for(int i = 0; i < 5; i++){
        for(int j = 0; j < status.status[i]; j++){
            for(int k = 0; k < 2; k++){
                GameObject before = status;
                if(before.move(i, j, mover[k])){
                    x[depth] = i;
                    y[depth] = j;
                    d[depth] = mover[k];
                    search(before, depth + 1);
                }
            }
        }
    }
}
int main(){
    freopen("mayan.in", "r", stdin);
    freopen("mayan.out", "w", stdout);
    init();
    search(starter, 1);
    printf("-1");
    return 0;
}