[数据结构]二叉树的旋转
在很多平衡树中都用到了树的旋转来维护,比如说红黑树,以及竞赛比较常用的树堆(Treap)
树的旋转既要能改变最大深度,使得平衡树平衡又不能破坏BST(二叉查找树,Binary Search Tree)
的性质,还是比较困难。
先不说BST的,先看看一棵普通的树是怎么旋转的(虽然是一样),然后再思考,为什么这样可以
不破坏BST的性质。
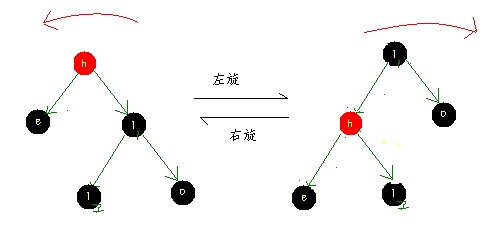
(PS,有两个结点的内容是一样,就在绘图的时候右边加了个标识)
虽然不太好看懂,那么就仔细观察吧(笑),那么就把木有怎么变的结点
标出来
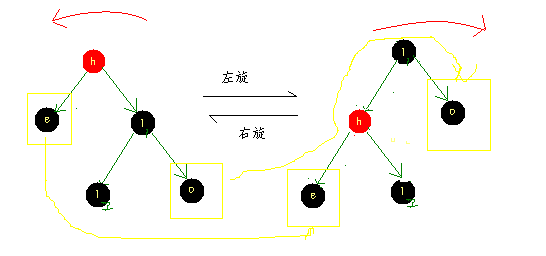
于是可以发现这几点
1)左旋前和左旋后原先根节点的左子树不会改变
2)左旋前和左旋后后来的根节点的右子树不会改变
3)右旋前和右旋后原先的根节点的右子树不会改变
4)右旋前和右旋后后来的根节点的左子树不会改变
(以上几点的前提是,你不用一维数组存树)
那再来看看改变的结点

先说左旋吧,新的根节点是原先根节点的右子树,原来的根节点变成新的根节点
的左子树,那新的根节点的原来的左子树去哪了?成了原来的根节点的右子树
右旋就和上面差不多了,自行琢磨一下很容易解决
接下来讲一下BST,我们将这几个会改变的结点进行编号,从上到下,标为1,2,3
根据BST的性质应该是结点1<结点3<结点2,将结点3变为结点1的右子树满足结点1<结点3,
结点1是结点2的左子树说明,结点1<结点2,结点3<结点2。满足这个条件
右旋和左旋仍然可以像这样理解。
Code
(我也不知道为什么突然想用java写了,如果是C/C++的同学看不懂的地方可以在评论问一下)
树的结点(PS,我养成了封装的好习惯)
TreeNode.java
package MyTree; /** * 树节点 **/ public class TreeNode<T> { private T data; private TreeNode<T> father; private TreeNode<T> left; private TreeNode<T> right; { father = null; left = null; right = null; } /** * 构造一个空的树节点 **/ public TreeNode(){ } /** * 构造一个拥有指定数据和父节点的节点 * @param data 指定的数据 * @param father 父节点的引用 **/ public TreeNode(T data, TreeNode<T> father){ this.data = data; this.father = father; } /** * 构造一个拥有指定数据、父节点和左右子树的<br> * 结点 * @param data 指定的数据 * @param father 父节点 * @param left 左子树 * @param right 右子树 */ public TreeNode(T data, TreeNode<T> father, TreeNode<T> left, TreeNode<T> right){ this.data = data; this.father = father; this.left = left; this.right = right; } /** * 以该节点作为根节点进行左旋 * @return 旋转成功返回true,<br> * 否则返回false */ public synchronized boolean rotateLeft(){ if(this.right == null) return false; TreeNode<T> buf = this.right; TreeNode<T> f = this.father; this.right = buf.left; this.father = buf; buf.left = this; buf.father = f; return true; } /** * 以该节点作为根节点进行右旋 * @return 旋转成功返回true,<br> * 否则返回false */ public synchronized boolean rotateRight(){ if(this.left == null) return false; TreeNode<T> buf = this.left; TreeNode<T> f = this.father; this.left = buf.right; this.father = buf; buf.right = this; buf.father = f; return true; } /** * @return the data */ public T getData() { return data; } /** * @param data the data to set */ public void setData(T data) { this.data = data; } /** * @return the father */ public TreeNode<T> getFather() { return father; } /** * @param father the father to set */ public void setFather(TreeNode<T> father) { this.father = father; } /** * @return the left */ public TreeNode<T> getLeft() { return left; } /** * @param left the left to set */ public void setLeft(TreeNode<T> left) { this.left = left; } /** * @return the right */ public TreeNode<T> getRight() { return right; } /** * @param right the right to set */ public void setRight(TreeNode<T> right) { this.right = right; } }
接下来按照上面的数据测试一下(当然啦,我也不能确保代码是正确的,如果您看出了什么问题可以在评论中指出)
TestRotate.java
1 package MyTree; 2 3 public class TestRotate { 4 5 protected static void preorder(TreeNode<? extends String> root){ 6 if(root == null) return; 7 System.out.print(root.getData()); 8 preorder(root.getLeft()); 9 preorder(root.getRight()); 10 } 11 12 public static void main(String[] args) { 13 14 @SuppressWarnings("unchecked") 15 TreeNode<String> nodes[] = new TreeNode[5]; 16 nodes[0] = new TreeNode<>("h", null); 17 nodes[1] = new TreeNode<>("e", nodes[0]); 18 nodes[0].setLeft(nodes[1]); 19 nodes[2] = new TreeNode<>("l", nodes[0]); 20 nodes[0].setRight(nodes[2]); 21 nodes[3] = new TreeNode<>("l", nodes[2]); 22 nodes[2].setLeft(nodes[3]); 23 nodes[4] = new TreeNode<>("o", nodes[2]); 24 nodes[2].setRight(nodes[4]); 25 26 preorder(nodes[0]); 27 28 nodes[0].rotateLeft(); 29 30 System.out.println(); 31 32 preorder(nodes[2]); 33 34 System.out.println(); 35 36 nodes[2].rotateRight(); 37 38 preorder(nodes[0]); 39 40 } 41 42 }
使用的时候请不要无视两段代码头的package,不然编译错误别怪我
(PS:这两段代码只在节点是根节点的时候不会出错,否则你可以看一下旋转一下是不是有节点
找不到了)

