loj 3285 「USACO 2020 US Open Platinum」Circus - 并查集 - 组合数学
题目传送门
显然当 $n = K$ 的时候,答案为 $K!$,下面将不再考虑。
考虑任选 $K$ 个位置,显然,任意一个初始状态都可以通过一些移动使得所有奶牛都在这 $K$ 个位置上。因此我们只统计这 $K$ 个位置上有多少种不同的初始状态。
考虑某个初始状态 $x$ 能够到达 $y$,那么相当于是对 $x$ 乘上了某一个置换 $f$。考虑两个属于不同的等价类的初始状态 $x, y$,如果我们把等价关系看做边,我们找一个生成树,显然我们能在两个连通块里找一个一样的生成树,因此如果在第一个等价类 $a$ 通过置换 $t$ 得到新的初始状态,那么和第二个等价类中和 $a$ 相应的状态通过置换 $t$ 也能得到新的初始状态。
因此所有等价类的大小都是相同的。因此答案是 $\frac{K!}{sz}$。
考虑怎么计算一个等价类的大小。考虑判断能不能交换两个位置上的奶牛,然后使得剩下的维持原状。
先考虑一些必要条件,注意到在任意度为 2 的点上不可能完成交换,考虑中间的点的度数都是 2,两端的点的度数都不是 2 的子图,下面我们称它为链。如果一侧子树内有 $A$ 个点,另一侧有 $B$ 个点,链上有 $C$ 个点,那么当 $K \geqslant (A - 1) + (B - 1)$,能够到达一侧的 $(A - 1)$ 个点始终不能到达另一侧,链上恰好始终有 $K - (A - 1) - (B - 1)$ 个点。
我们来证明当不违反上述条件时,可以完成交换。即不穿过满足 $K \geqslant (A - 1) + (B - 1)$ 的链,能够使得它们互相到达。
先考虑将某一个奶牛移动到右侧。先考虑两端的度数都大于等于 $3$ 的情形。
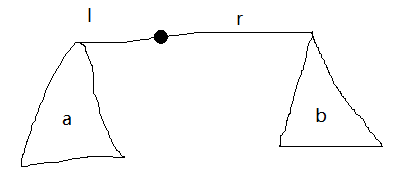
假设左侧在链上有 $l$ 个点,子树内(不含根)有 $a$ 个点,右侧链上有 $r$ 个点,右侧子树内有 $b$ 个点。根据条件有 $a + l + r + b + 1 < (A - 1) + (B - 1)$。
- 如果 $r + b < B - 1$ 直接移过去就完事了。
- 否则有 $a + l < A - 2$,
- 如果和奶牛相连的空位子形成一条链,那么找一个子树内不在链上的奶牛移到链上,然后把这个奶牛移动到这个位置上,然后把剩下的奶牛往子树内移动,直到 $r + b < B - 1$。
- 否则随意移动到一棵子树内,然后将在链上的下一个点移开,直到形成一条链或者 $r + b < B - 1$。
当一端度数为 $1$,有 $r + b + 1 < B - 1$,显然可行。
然后考虑完成交换,这个时候只用证明任意两个链上相邻的奶牛可以交换位置就可以了。此时满足 $a + l + r + b + 2 < (A - 1) + (B - 1)$。即 $a + l + r + b < A + B - 4$,此时要么 $a + l \leqslant A - 3$,要么 $b + r \leqslant B - 3$。不妨设是 $a + l \leqslant A - 3$,这个时候只用将 $l$ 个奶牛全部移动到子树内,如果使得空的位置形成了一条链,那么把一个不在链上的奶牛,移到链上就可以了。然后再子树中剩下至少 3 个空位可以完成交换。
现在来说明一下可以使得剩下的奶牛位置不变,注意到操作总是可逆的,$x, y$ 交换完成后,把 $y$ 看成 $x$,把 $x$ 看成 $y$,因为存在初始状态到达它的方案,所以也存在它到初始状态的方案,操作结束后 $x, y$ 的位置是相反的。
如果两个位置能交换,那么它们连一条边,$sz = \prod s_i!$,$s_i$ 是每个连通块的大小。
然后从大到小枚举 $K$ ,如果一条链满足 $K < (A - 1) + (B - 1)$ 就把它两端连接上。然后问题变成能够到达每个连通块的有多少点。直接做不好做,但根据和它相邻的被断掉的边计算不能到它的点有多少个,把它们减去就行了。
另外注意到连通块数等于链数加一,一条链在存在的次数等于它的链长,所以对于每个 $K$ 暴力枚举所有连通块复杂度为 $O(n)$。剩下的并查集维护即可。
时间复杂度 $O(n\log n)$。
Code
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;
#define ll long long
void exgcd(int a, int b, int& x, int& y) {
if (!b) {
x = 1, y = 0;
} else {
exgcd(b, a % b, y, x);
y -= (a / b) * x;
}
}
int inv(int a, int n) {
int x, y;
exgcd(a, n, x, y);
return (x < 0) ? (x + n) : (x);
}
const int Mod = 1e9 + 7;
template <const int Mod = :: Mod>
class Z {
public:
int v;
Z() : v(0) { }
Z(int x) : v(x){ }
Z(ll x) : v(x % Mod) { }
friend Z operator + (const Z& a, const Z& b) {
int x;
return Z(((x = a.v + b.v) >= Mod) ? (x - Mod) : (x));
}
friend Z operator - (const Z& a, const Z& b) {
int x;
return Z(((x = a.v - b.v) < 0) ? (x + Mod) : (x));
}
friend Z operator * (const Z& a, const Z& b) {
return Z(a.v * 1ll * b.v);
}
friend Z operator ~(const Z& a) {
return inv(a.v, Mod);
}
friend Z operator - (const Z& a) {
return Z(0) - a;
}
Z& operator += (Z b) {
return *this = *this + b;
}
Z& operator -= (Z b) {
return *this = *this - b;
}
Z& operator *= (Z b) {
return *this = *this * b;
}
friend boolean operator == (const Z& a, const Z& b) {
return a.v == b.v;
}
};
Z<> qpow(Z<> a, int p) {
Z<> rt = Z<>(1), pa = a;
for ( ; p; p >>= 1, pa = pa * pa) {
if (p & 1) {
rt = rt * pa;
}
}
return rt;
}
typedef Z<> Zi;
typedef class Path {
public:
int u, v, su, sv, sab;
Path(int u, int v, int su, int sv) : u(u), v(v), su(su), sv(sv), sab(su + sv - 2) { }
bool operator < (Path b) const {
return sab > b.sab;
}
} Path;
const int N = 1e5 + 5;
int n;
vector<int> G[N];
Zi fac[N], _fac[N];
void init_fac(int n) {
fac[0] = 1;
for (int i = 1; i <= n; i++) {
fac[i] = fac[i - 1] * i;
}
_fac[n] = ~fac[n];
for (int i = n; i; i--) {
_fac[i - 1] = _fac[i] * i;
}
}
int sz[N];
vector<Path> P;
int get_sz(int p, int fa) {
sz[p] = 1;
for (auto e : G[p]) {
if (e ^ fa) {
sz[p] += get_sz(e, p);
}
}
return sz[p];
}
void dfs(int p, int fa, int u, int su) {
if (G[p].size() ^ 2u) {
if (u) {
P.emplace_back(u, p, su, sz[p]);
}
for (auto e : G[p]) {
if (e ^ fa) {
dfs(e, p, p, n - sz[e]);
}
}
} else {
for (auto e : G[p]) {
if (e ^ fa) {
dfs(e, p, u, su);
}
}
}
}
int uf[N];
int f[N], g[N];
int pre[N], suf[N];
void remove(int x) {
pre[suf[x]] = pre[x];
suf[pre[x]] = suf[x];
}
int find(int x) {
return uf[x] == x ? x : (uf[x] = find(uf[x]));
}
void merge(Path p) {
int u = p.u, v = p.v;
int fu = find(u);
int fv = find(v);
f[fu]--, f[fv]--;
g[fu] -= p.su - 1, g[fv] -= p.sv - 1;
f[fu] += f[fv];
g[fu] += g[fv];
uf[fv] = fu;
}
Zi ans[N];
int main() {
scanf("%d", &n);
for (int i = 1, u, v; i < n; i++) {
scanf("%d%d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
init_fac(n);
int Rt = 1;
while (G[Rt].size() == 2u) Rt++;
get_sz(Rt, 0);
dfs(Rt, 0, 0, 0);
sort(P.begin(), P.end());
pre[0] = 0, suf[0] = 1;
for (int i = 1; i <= n; i++) {
pre[i] = i - 1, suf[i] = i + 1;
}
pre[n + 1] = n, suf[n + 1] = n + 1;
for (int i = 1; i <= n; i++) {
if (G[i].size() == 2u) {
remove(i);
} else {
uf[i] = i;
}
}
for (auto p : P) {
f[p.u]++, f[p.v]++;
g[p.u] += p.su - 1;
g[p.v] += p.sv - 1;
}
auto it = P.begin(), _it = P.end();
for (int k = n - 1; k; k--) {
while (it != _it && (*it).sab > k) {
merge(*it);
it++;
}
ans[k] = fac[k];
for (int i = suf[0]; i <= n; i = suf[i]) {
if (find(i) != i) {
remove(i);
continue;
}
int t = k - k * f[i] + g[i];
ans[k] *= _fac[t];
}
}
ans[n] = fac[n];
for (int i = 1; i <= n; i++) {
printf("%d\n", ans[i].v);
}
return 0;
}
