loj 3090 「BJOI2019」勘破神机 - 数学 - 多项式
题目传送门
题目大意
设$F_{n}$表示用$1\times 2$的骨牌填$2\times n$的网格的方案数,设$G_{n}$表示用$1\times 2$的骨牌填$3\times n$的网格的方案数.
- 给定$l, r, k$,求$\frac{1}{r - l + 1}\sum_{i = l}^{r} \binom{F_{i}}{k}$.
- 给定$l, r, k$,求$\frac{1}{r - l + 1}\sum_{i = l}^{r} \binom{G_{i}}{k}$.
之前好像在loj / uoj群上问过求Fibonacci求立方和。sad。。。
校内考的时候忘了求数列通项,sad。。。
首先用Stirling数把组合数拆成通常幂。
对于第一部分,直接用$Fibonacci$通项,由于$5$不是模$998244353$的二次剩余,所以把答案在运算中表示成$a + b\sqrt{5}$的形式。
第$n$项的$k$次幂大概是$(a^n + b^n)^{K}$,这个不方便直接求和。用二项式定理展开就行了。
对于第二部分。考察选手是否上过高考数学课(bushi
显然当$2 \nmid n$时$G_{n} = 0$,现在考虑$G'_{n} = G_{2n}$。
注意到最后只有这几种填法:
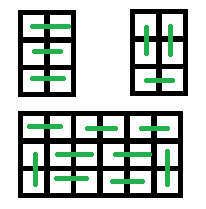
所以有
$$
\begin{align}
G'_{n} &= 3G_{n - 1} + 2\sum_{i = 0}^{n - 2}G_{i} \\
&= 4G_{n - 1} - 3G_{n - 2} - 2\sum_{i = 0}^{n - 3} G_{i - 1} + 2\sum_{i =0}^{n - 2}G_i \\
&= 4G_{n - 1} - G_{n - 2}
\end{align}
$$
用特征根法推通项(不会的话可以回教室了)。然后做完了。
(我被Jode锤爆了。瑟瑟发抖.jpg)
Code
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;
#define ll long long
void exgcd(int a, int b, int& x, int& y) {
if (!b) {
x = 1, y = 0;
} else {
exgcd(b, a % b, y, x);
y -= (a / b) * x;
}
}
int inv(int a, int n) {
int x, y;
exgcd(a, n, x, y);
return (x < 0) ? (x + n) : (x);
}
const int Mod = 998244353;
template <const int Mod = :: Mod>
class Z {
public:
int v;
Z() : v(0) { }
Z(int x) : v(x){ }
Z(ll x) : v(x % Mod) { }
friend Z operator + (const Z& a, const Z& b) {
int x;
return Z(((x = a.v + b.v) >= Mod) ? (x - Mod) : (x));
}
friend Z operator - (const Z& a, const Z& b) {
int x;
return Z(((x = a.v - b.v) < 0) ? (x + Mod) : (x));
}
friend Z operator * (const Z& a, const Z& b) {
return Z(a.v * 1ll * b.v);
}
friend Z operator ~(const Z& a) {
return inv(a.v, Mod);
}
friend Z operator - (const Z& a) {
return Z(0) - a;
}
Z& operator += (Z b) {
return *this = *this + b;
}
Z& operator -= (Z b) {
return *this = *this - b;
}
Z& operator *= (Z b) {
return *this = *this * b;
}
friend boolean operator == (const Z& a, const Z& b) {
return a.v == b.v;
}
};
Z<> qpow(Z<> a, int p) {
Z<> rt = Z<>(1), pa = a;
for ( ; p; p >>= 1, pa = pa * pa) {
if (p & 1) {
rt = rt * pa;
}
}
return rt;
}
typedef Z<> Zi;
template <const int I>
class ComplexTemp {
public:
Zi r, v;
ComplexTemp() : r(0), v(0) { }
ComplexTemp(Zi r) : r(r), v(0) { }
ComplexTemp(Zi r, Zi v) : r(r), v(v) { }
friend ComplexTemp operator + (const ComplexTemp& a, const ComplexTemp& b) {
return ComplexTemp(a.r + b.r, a.v + b.v);
}
friend ComplexTemp operator - (const ComplexTemp& a, const ComplexTemp& b) {
return ComplexTemp(a.r - b.r, a.v - b.v);
}
friend ComplexTemp operator - (const ComplexTemp& a, const int& b) {
return ComplexTemp(a.r - b, a.v);
}
friend ComplexTemp operator * (const ComplexTemp& a, const ComplexTemp& b) {
return ComplexTemp(a.r * b.r + a.v * b.v * I, a.r * b.v + a.v * b.r);
}
friend ComplexTemp operator * (const ComplexTemp& a, const Zi& x) {
return ComplexTemp(a.r * x, a.v * x);
}
friend ComplexTemp operator / (const ComplexTemp& a, const ComplexTemp& b) {
ComplexTemp c = b.conj();
return a * c * ~((b * c).r);
}
ComplexTemp conj() const {
return ComplexTemp(r, -v);
}
boolean operator == (ComplexTemp b) {
return r == b.r && v == b.v;
}
};
const int Kmx = 510;
Zi s1[Kmx][Kmx];
Zi comb[Kmx][Kmx];
Zi fac[Kmx], _fac[Kmx];
void prepare(int n) {
fac[0] = 1;
for (int i = 1; i <= n; i++) {
fac[i] = fac[i - 1] * i;
}
_fac[n] = ~fac[n];
for (int i = n; i; i--) {
_fac[i - 1] = _fac[i] * i;
}
s1[0][0] = 1;
for (int i = 1; i <= n; i++) {
s1[i][0] = 0, s1[i][i] = 1;
for (int j = 1; j < i; j++) {
s1[i][j] = s1[i - 1][j - 1] + s1[i - 1][j] * (i - 1);
}
}
comb[0][0] = 1;
for (int i = 1; i <= n; i++) {
comb[i][0] = comb[i][i] = 1;
for (int j = 1; j < i; j++) {
comb[i][j] = comb[i - 1][j - 1] + comb[i - 1][j];
}
}
}
template <typename T>
T qpow(T a, ll p) {
T rt = Zi(1), pa = a;
for ( ; p; p >>= 1, pa = pa * pa) {
if (p & 1) {
rt = rt * pa;
}
}
return rt;
}
namespace subtask1 {
typedef ComplexTemp<5> Complex;
const Zi inv2 ((Mod + 1) >> 1);
const Complex q1 (inv2, inv2), q2 (inv2, -inv2);
Complex pwq1[Kmx], pwq2[Kmx], pwqq[Kmx][Kmx];
Complex get_sum(int k1, int k2, ll n) {
Complex x = pwq1[k1] * pwq2[k2];
if (x == Zi(1))
return Zi(n);
return (pwqq[k1][k2] - 1) / (x - 1);
}
inline void init() {
pwq1[0] = pwq2[0] = Zi(1);
for (int i = 1; i < Kmx; i++) {
pwq1[i] = pwq1[i - 1] * q1;
pwq2[i] = pwq2[i - 1] * q2;
}
}
Zi work(ll n, int K) {
Complex coef = qpow(Complex(0, ~Zi(5)), K);
Complex ret (0, 0);
for (int k = 0; k <= K; k++) {
// Complex tmp = get_sum(pwq1[k] * pwq2[K - k], n) * comb[K][k];
Complex tmp = get_sum(k, K - k, n) * comb[K][k];
if ((K - k) & 1) {
ret = ret - tmp;
} else {
ret = ret + tmp;
}
}
ret = ret * coef;
assert(ret.v.v == 0);
// cerr << n << " " << K << " " << ret.r.v << '\n';
return ret.r;
}
Zi solve(ll n, int K) {
Zi ans = 0;
Complex q1n = qpow(q1, n + 1);
Complex q2n = qpow(q2, n + 1);
pwqq[0][0] = Zi(1);
for (int i = 0; i <= K; i++) {
for (int j = (i == 0); i + j <= K; j++) {
pwqq[i][j] = ((!i) ? (pwqq[i][j - 1] * q2n) : (pwqq[i - 1][j] * q1n));
}
}
for (int i = 1; i <= K; i++) {
Zi tmp = work(n, i) * s1[K][i] * _fac[K];
if ((K - i) & 1) {
ans -= tmp;
} else {
ans += tmp;
}
}
return ans;
}
void __main__(ll l, ll r, int K) {
++l, ++r;
Zi ans = solve(r, K) - solve(l - 1, K);
ans = ans * ~Zi(r - l + 1);
printf("%d\n", ans.v);
}
}
namespace subtask2 {
typedef ComplexTemp<3> Complex;
const Zi inv2 ((Mod + 1) >> 1);
const Zi inv3 ((Mod + 1) / 3);
const Zi inv6 = inv2 * inv3;
const Complex c1 (inv2, -inv6), c2 (inv2, inv6);
const Complex q1 (2, Mod - 1), q2 (2, 1);
Complex pwq1[Kmx], pwq2[Kmx], pwc1[Kmx], pwc2[Kmx];
Complex pwqq[Kmx][Kmx];
Complex get_sum(int k1, int k2, ll n) {
Complex x = pwq1[k1] * pwq2[k2];
if (x == Zi(1))
return Zi(n);
return (pwqq[k1][k2] - 1) / (x - 1);
}
inline void init() {
pwq1[0] = pwq2[0] = pwc1[0] = pwc2[0] = Zi(1);
for (int k = 1; k < Kmx; k++) {
pwq1[k] = pwq1[k - 1] * q1;
pwq2[k] = pwq2[k - 1] * q2;
pwc1[k] = pwc1[k - 1] * c1;
pwc2[k] = pwc2[k - 1] * c2;
}
}
Zi work(ll n, int K) {
Complex ret (0, 0);
for (int k = 0; k <= K; k++) {
Complex tmp = get_sum(k, K - k, n) * comb[K][k];
Complex b = pwc1[k] * pwc2[K - k];
tmp = tmp * b;
ret = ret + tmp;
}
assert(ret.v.v == 0);
// cerr << n << " " << K << " " << ret.r.v << '\n';
return ret.r;
}
Zi solve(ll n, int K) {
n >>= 1;
Zi ans = 0;
Complex q1n = qpow(q1, n + 1);
Complex q2n = qpow(q2, n + 1);
pwqq[0][0] = Zi(1);
for (int i = 0; i <= K; i++) {
for (int j = (i == 0); i + j <= K; j++) {
pwqq[i][j] = ((!i) ? (pwqq[i][j - 1] * q2n) : (pwqq[i - 1][j] * q1n));
}
}
for (int i = 1; i <= K; i++) {
Zi tmp = work(n, i) * s1[K][i] * _fac[K];
if ((K - i) & 1) {
ans -= tmp;
} else {
ans += tmp;
}
}
return ans;
}
void __main__(ll l, ll r, int K) {
Zi ans = solve(r, K) - solve(l - 1, K);
ans = ans * ~Zi(r - l + 1);
printf("%d\n", ans.v);
}
}
int Case, ___;
ll l, r;
int K;
int main() {
prepare(502);
scanf("%d%d", &Case, &___);
if (___ == 3) {
subtask2::init();
} else {
subtask1::init();
}
while (Case--) {
scanf("%lld%lld%d", &l, &r, &K);
if (___ == 2) {
subtask1::__main__(l, r, K);
} else {
subtask2::__main__(l, r, K);
}
}
return 0;
}
然而注意到两个特征根的积不是 1 就是 -1,那么假设乘积是 1,考虑暴力展开 $(\lambda_1 \alpha^n + \lambda_2 \alpha^{-n})^{\overline{K}}$ 。
把 $\alpha^{n}$ 看做 $x$,大力分治 FFT。考虑最外层的求和符号后每一项变成 $\sum \alpha^{ni}$,简单算一下就行了。
如果乘积是 $-1$ 讨论一下奇偶性就行了。
时间复杂度 $O(K \log^2 K + K \log r)$
Code
#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;
#define ll long long
void exgcd(int a, int b, int& x, int& y) {
if (!b) {
x = 1, y = 0;
} else {
exgcd(b, a % b, y, x);
y -= (a / b) * x;
}
}
int inv(int a, int n) {
int x, y;
exgcd(a, n, x, y);
return (x < 0) ? (x + n) : (x);
}
const int N = 262144;
const int Mod = 998244353;
const int bzmax = 19;
const int g = 3;
template <const int Mod = :: Mod>
class Z {
public:
int v;
Z() : v(0) { }
Z(int x) : v(x){ }
Z(ll x) : v(x % Mod) { }
friend Z operator + (const Z& a, const Z& b) {
int x;
return Z(((x = a.v + b.v) >= Mod) ? (x - Mod) : (x));
}
friend Z operator - (const Z& a, const Z& b) {
int x;
return Z(((x = a.v - b.v) < 0) ? (x + Mod) : (x));
}
friend Z operator * (const Z& a, const Z& b) {
return Z(a.v * 1ll * b.v);
}
friend Z operator ~(const Z& a) {
return inv(a.v, Mod);
}
friend Z operator - (const Z& a) {
return Z(0) - a;
}
Z& operator += (Z b) {
return *this = *this + b;
}
Z& operator -= (Z b) {
return *this = *this - b;
}
Z& operator *= (Z b) {
return *this = *this * b;
}
friend boolean operator == (const Z& a, const Z& b) {
return a.v == b.v;
}
};
typedef Z<> Zi;
template <const int I>
class ComplexTemp {
public:
Zi r, v;
ComplexTemp() : r(0), v(0) { }
ComplexTemp(int r) : r(r), v(0) { }
ComplexTemp(Zi r) : r(r), v(0) { }
ComplexTemp(Zi r, Zi v) : r(r), v(v) { }
friend ComplexTemp operator + (ComplexTemp a, ComplexTemp b) {
return ComplexTemp(a.r + b.r, a.v + b.v);
}
friend ComplexTemp operator - (ComplexTemp a, ComplexTemp b) {
return ComplexTemp(a.r - b.r, a.v - b.v);
}
friend ComplexTemp operator * (ComplexTemp a, ComplexTemp b) {
return ComplexTemp(a.r * b.r + a.v * b.v * I, a.r * b.v + a.v * b.r);
}
friend ComplexTemp operator / (ComplexTemp a, ComplexTemp b) {
ComplexTemp c = b.conj();
return a * c * ~((b * c).r);
}
friend ComplexTemp operator - (ComplexTemp a) {
return ComplexTemp(-a.r, -a.v);
}
ComplexTemp conj() const {
return ComplexTemp(r, -v);
}
friend ComplexTemp operator ~ (ComplexTemp a) {
return ComplexTemp(1) / a;
}
boolean operator == (ComplexTemp b) {
return r == b.r && v == b.v;
}
ComplexTemp& operator -= (ComplexTemp b) {
return *this = *this - b;
}
ComplexTemp& operator += (ComplexTemp b) {
return *this = *this + b;
}
ComplexTemp& operator *= (ComplexTemp b) {
return *this = *this * b;
}
};
template <typename T>
T qpow(T a, ll p) {
if (p < 0) {
a = ~a;
p = -p;
}
T rt (1);
for ( ; p; p >>= 1, a = a * a) {
if (p & 1) {
rt = rt * a;
}
}
return rt;
}
class NTT {
private:
Zi gn[bzmax + 4], _gn[bzmax + 4];
public:
NTT() {
for (int i = 0; i <= bzmax; i++) {
gn[i] = qpow(Zi(g), (Mod - 1) >> i);
_gn[i] = qpow(Zi(g), -((Mod - 1) >> i));
}
}
template <typename T>
void operator () (T* f, int len, int sgn) {
for (int i = 1, j = len >> 1, k; i < len - 1; i++, j += k) {
if (i < j)
swap(f[i], f[j]);
for (k = len >> 1; k <= j; j -= k, k >>= 1);
}
Zi *wn = (sgn > 0) ? (gn + 1) : (_gn + 1), w;
T a, b;
for (int l = 2, hl; l <= len; l <<= 1, wn++) {
hl = l >> 1, w = 1;
for (int i = 0; i < len; i += l, w = 1) {
for (int j = 0; j < hl; j++, w *= *wn) {
a = f[i + j], b = f[i + j + hl] * w;
f[i + j] = a + b;
f[i + j + hl] = a - b;
}
}
}
if (sgn < 0) {
Zi invlen = ~Zi(len);
for (int i = 0; i < len; i++) {
f[i] *= invlen;
}
}
}
int correct_len(int len) {
int m = 1;
for ( ; m <= len; m <<= 1);
return m;
}
} NTT;
const Zi inv2 = (Mod + 1) >> 1;
namespace subtask1 {
typedef ComplexTemp<5> Complex;
typedef class Poly : public vector<Complex> {
public:
using vector<Complex>::vector;
Poly& fix(int sz) {
resize(sz);
return *this;
}
} Poly;
Poly operator * (Poly A, Poly B) {
int n = A.size(), m = B.size();
int k = NTT.correct_len(n + m - 1);
if (n < 20 || m < 20) {
Poly rt (n + m - 1, Complex(0, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
rt[i + j] += A[i] * B[j];
}
}
return rt;
}
A.resize(k), B.resize(k);
NTT(A.data(), k, 1);
NTT(B.data(), k, 1);
for (int i = 0; i < k; i++) {
A[i] *= B[i];
}
NTT(A.data(), k, -1);
A.resize(n + m - 1);
return A;
}
const Complex alpha (inv2, inv2), lambda (0, ~Zi(5));
int K;
Poly f1, f2;
Poly dividing(int l, int r, int coef) {
if (l == r) {
return Poly {(coef == 1) ? lambda : -lambda, -Zi(l), lambda};
}
int mid = (l + r) >> 1;
return dividing(l, mid, coef) * dividing(mid + 1, r, coef);
}
void prepare(int _K) {
K = _K;
f1 = dividing(0, K - 1, 0);
f2 = dividing(0, K - 1, 1);
}
Zi calc(ll n) {
auto calc = [&] (Complex a, ll n) {
return (a == Complex(1)) ? (Complex(Zi((n + 1) % Mod))) : ((qpow(a, n + 1) - 1) / (a - 1));
};
Complex ans (0);
for (int i = 0, _ = f1.size(); i < _; i++) {
Complex z = qpow(alpha, (i - K));
ans = ans + calc(z * z, n >> 1) * f1[i];
}
for (int i = 0, _ = f2.size(); i < _; i++) {
Complex z = qpow(alpha, (i - K));
ans = ans + calc(z * z, (n - 1) >> 1) * f2[i] * z;
}
assert(!ans.v.v);
Zi fac = 1;
for (int i = 1; i <= K; i++) {
fac *= i;
}
ans.r *= ~fac;
return ans.r;
}
Zi calc(ll l, ll r, int _K) {
prepare(_K);
return (calc(r + 1) - calc(l)) * ~Zi(r - l + 1);
}
}
namespace subtask2 {
typedef ComplexTemp<3> Complex;
typedef class Poly : public vector<Complex> {
public:
using vector<Complex>::vector;
Poly& fix(int sz) {
resize(sz);
return *this;
}
} Poly;
Poly operator * (Poly A, Poly B) {
int n = A.size(), m = B.size();
int k = NTT.correct_len(n + m - 1);
if (n < 20 || m < 20) {
Poly rt (n + m - 1, Complex(0, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
rt[i + j] += A[i] * B[j];
}
}
return rt;
}
A.resize(k), B.resize(k);
NTT(A.data(), k, 1);
NTT(B.data(), k, 1);
for (int i = 0; i < k; i++) {
A[i] *= B[i];
}
NTT(A.data(), k, -1);
A.resize(n + m - 1);
return A;
}
const Zi inv2 ((Mod + 1) >> 1);
const Zi inv3 ((Mod + 1) / 3);
const Zi inv6 = inv2 * inv3;
const Complex lambda1 (inv2, -inv6), lambda2 (inv2, inv6);
const Complex alpha (2, Mod - 1);
int K;
Poly f;
Poly dividing(int l, int r) {
if (l == r) {
return Poly {lambda2, -Zi(l), lambda1};
}
int mid = (l + r) >> 1;
return dividing(l, mid) * dividing(mid + 1, r);
}
void prepare(int _K) {
K = _K;
f = dividing(0, K - 1);
}
Zi calc(ll n) {
n >>= 1;
auto calc = [&] (Complex a, ll n) {
return (a == Complex(1)) ? (Complex(Zi((n + 1) % Mod))) : ((qpow(a, n + 1) - 1) / (a - 1));
};
Complex ans (0);
for (int i = 0, _ = f.size(); i < _; i++) {
Complex z = qpow(alpha, (i - K));
ans = ans + calc(z, n) * f[i];
}
assert(!ans.v.v);
Zi fac = 1;
for (int i = 1; i <= K; i++) {
fac *= i;
}
ans.r *= ~fac;
return ans.r;
}
Zi calc(ll l, ll r, int _K) {
prepare(_K);
return (calc(r) - calc(l - 1)) * ~Zi(r - l + 1);
}
}
int main() {
ios::sync_with_stdio(false);
int type, T;
cin >> T >> type;
ll l, r, K;
while (T--) {
cin >> l >> r >> K;
Zi ans = type == 2 ? subtask1::calc(l, r, K) : subtask2::calc(l, r, K);
printf("%d\n", ans.v);
}
return 0;
}

