2018年山东省省队集训 Round 1 Day 2简要题解
(相信来看这篇博客的人都有题面)
T2以为可以线性递推,然后花了两个小时。然后想了两个小时T1,会了一个能过的算法。但是没时间写,sad.....比赛快结束时,发现T2模数$10^9+7$,内心mmp。
Problem A 生日礼物
题目大意
给定一个$n\times m$的网格图,每个格子中有一个不是0就是1的数,要求对于任意$w\times h$的子矩阵的和都相等,问方案数。
(为了简洁,各式子的范围请自行脑补)
瞎推推不难发现对于一个格子$(x, y)$,满足$a_{x, y} + a_{x + w, y + h} = a_{x + w, y} + a_{x, y + h}$。
移项得:
$\begin{align}a_{x, y} - a_{x + w, y} = a_{x, y + h} - a_{x + w, y + h}\end{align}$
用归纳法能够得出对于每连续的$w + 1$行,对模$h$的剩余相同的列,这$w + 1$行中的第一行和最后一行的上的数之差相等。
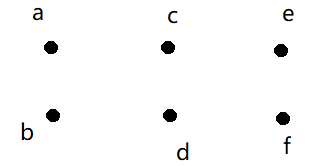
对于上图来说就是$a - b = c - d = e - f$。
考虑先确定前$w$行,每次在后面添加一行。显然这一行我们只用考虑前$h$个数(剩下的用式$(1)$来确定)。
考虑每一处$(i, j)$和它上面第$w$个格子上的数的差$d$
- 若$d = 1$,则说明$a_{i - w, j + kh} = 0 (k = 0, 1, \dots)$
- 若$d = 0$,则什么都不能说明
- 若$d = -1$,则说明$a_{i - w, j + kh} = 1 (k = 0, 1, \dots)$
所以变化量能为$1,-1$的只有当这一行上纵坐标模$h$同余于它的位置上的数等于它。
然后发现只要确定左上角的$w\times h$的矩形的状况,剩下的就能用快速幂计算。
然后我的做法就比较沙雕了。
$f_{s}$表示恰好包含$s$中的位置作为横着相同的格子,且将前$w$行填满的方案数。(不考虑这些格子上的数)
这个首先需要考虑这些格子上的数,进行容斥和子集和变换,再将这些格子上的数的贡献减去。
然后单独考虑这个矩阵中每一行的贡献,枚举$0$和$1$的数量,就可以计算贡献了。
Code

1 #include <iostream> 2 #include <cassert> 3 #include <cstdlib> 4 #include <cstdio> 5 using namespace std; 6 typedef bool boolean; 7 8 const int Mod = 1e9 + 7; 9 10 int add(int a, int b) { 11 return ((a += b) >= Mod) ? (a - Mod) : (a); 12 } 13 14 int sub(int a, int b) { 15 return ((a -= b) < 0) ? (a + Mod) : (a); 16 } 17 18 int mul(int a, int b) { 19 return a * 1ll * b % Mod; 20 } 21 22 int qpow(int a, int p) { 23 int rt = 1, pa = a; 24 for ( ; p; p >>= 1, pa = mul(pa, pa)) 25 if (p & 1) 26 rt = mul(rt, pa); 27 return rt; 28 } 29 30 const int S = 1 << 16; 31 32 int n, m, w, h; 33 int f[S], bit[S]; 34 int c[5][5], sc[5][5]; 35 int d[5][5], sd[5][5]; 36 int comb[5][5] = {{1, 0, 0, 0, 0}, {1, 1, 0, 0, 0}, {1, 2, 1, 0, 0}, {1, 3, 3, 1, 0}, {1, 4, 6, 4, 1}}; 37 int invs[17]; 38 39 inline void init() { 40 scanf("%d%d%d%d", &n, &m, &w, &h); 41 } 42 43 int getline(int s, int l) { 44 int rt = (s >> l) & 1; 45 for (int i = 1; i < w; i++) 46 rt = (((s >> (h * i + l)) & 1) << i) | rt; 47 return rt; 48 } 49 50 int getrow(int s, int row) { 51 int msk = (1 << h) - 1; 52 return s >> (h * row) & msk; 53 } 54 55 inline void solve() { 56 d[0][0] = 1; 57 for (int i = 0; i < 4; i++) 58 for (int j = 0; j <= i; j++) { 59 d[i + 1][j] = add(d[i + 1][j], d[i][j]); 60 d[i + 1][j + 1] = add(d[i + 1][j + 1], d[i][j]); 61 } 62 63 int sl_repeat = m / h; 64 for (int i = 0; i <= 4; i++) 65 for (int j = 0; j <= i; j++) 66 sd[i][j] = qpow(d[i][j], sl_repeat); 67 68 bit[0] = 0; 69 for (int i = 0; i < S; i++) 70 bit[i] = bit[i >> 1] + (i & 1); 71 72 int all = 1 << (w * h); 73 for (int s = 0; s < all; s++) { 74 f[s] = (1 << bit[s]); 75 for (int l = 0; l < h; l++) { 76 int sl = getline(s, l); 77 int blank = w - bit[sl]; 78 int cmp = 0; 79 boolean aflag = ((m % h) > l); 80 for (int i = 0; i <= blank; i++) 81 cmp = add(mul(sd[blank][i], (aflag) ? (d[blank][i]) : (1)), cmp); 82 f[s] = mul(f[s], cmp); 83 } 84 } 85 86 int size = w * h; 87 for (int i = 0; i < size; i++) 88 for (int j = 0; j < all; j++) 89 if (!((j >> i) & 1)) 90 f[j] = sub(f[j], f[j ^ (1 << i)]); 91 92 for (int k = 0; k <= 4; k++) 93 for (int c0 = 0; c0 <= k; c0++) { 94 int c1 = k - c0, ava = min(c0, c1); 95 int& res = c[c0][c1]; 96 for (int use = 0; use <= ava; use++) { 97 // res = add(res, mul(comb[c0][use], mul(comb[c1][use], fac[use]))); 98 res = add(res, mul(comb[c0][use], comb[c1][use])); 99 } 100 sc[c0][c1] = qpow(res, n / w - 1); 101 } 102 103 invs[0] = 1; 104 for (int i = 1; i <= 16; i++) 105 invs[i] = qpow(1 << i, Mod - 2); 106 for (int i = 0; i < all; i++) 107 f[i] = mul(f[i], invs[bit[i]]); 108 109 int res = 0; 110 for (int s = 0; s < all; s++) { 111 if (!f[s]) 112 continue; 113 int tmp = 1; 114 for (int r = 0; r < w; r++) { 115 int sr = getrow(s, r); 116 int spe = bit[sr], cmp = 0; 117 boolean aflag = ((n % w) > r); 118 for (int c0 = 0; c0 <= spe; c0++) { 119 cmp = add(cmp, mul(mul(::sc[c0][spe - c0], ((aflag) ? (c[c0][spe - c0]) : (1))), comb[spe][c0])); 120 } 121 tmp = mul(tmp, cmp); 122 // cerr << sr << " " << s << " " << r << " " << cmp << '\n'; 123 } 124 // if (tmp && f[s]) 125 // cerr << s << " " << mul(f[s], tmp) << '\n'; 126 res = add(res, mul(f[s], tmp)); 127 } 128 printf("%d\n", res); 129 } 130 131 int main() { 132 init(); 133 solve(); 134 return 0; 135 }
Problem B 咕咕
题目大意
有$n$种物品,每种物品无限个,第$i$种物品的体积为$a_i$。设$f(n)$表示恰好填满容量为$n$的背包的方案数,求$\sum_{i = L}^{R}f(i)$。
(这道题的名称告诉了我们不想掉rating的正确做法)
(我们可以线性递推 + 三模数NTT)
考虑每加入一个物品相当于对模$a_i$同余于$j\ (j = 0, 1, \dots, a_i - 1)$的地方分别做一次前缀和。
所以对于模$[a_{1}, a_{2}, \cdots, a_{n}]$余$r$的地方可以用一个$n - 1$次多项式表示。
由于要求前缀和,就再加入体积为$1$的物品。
对于$L-1,R$处的取值直接用$Lagrange$插值。
Code

1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 using namespace std; 5 typedef bool boolean; 6 7 #define ll long long 8 9 const int N = 11, S = 100001 * N; 10 const int Mod = 1e9 + 7; 11 12 int add(int a, int b) { 13 return ((a += b) >= Mod) ? (a - Mod) : (a); 14 } 15 16 int sub(int a, int b) { 17 return ((a -= b) < 0) ? (a + Mod) : (a); 18 } 19 20 int mul(int a, int b) { 21 return a * 1ll * b % Mod;; 22 } 23 24 void exgcd(int a, int b, int& x, int& y) { 25 if (!b) 26 x = 1, y = 0; 27 else { 28 exgcd(b, a % b, y, x); 29 y -= (a / b) * x; 30 } 31 } 32 33 int inv(int a, int n) { 34 int x, y; 35 exgcd(a, n, x, y); 36 return (x < 0) ? (x + n) : (x); 37 } 38 39 int n, prod = 1, m; 40 int a[N], f[S]; 41 42 inline void init() { 43 scanf("%d", &n); 44 for (int i = 0; i < n; i++) 45 scanf("%d", a + i), prod *= a[i]; 46 m = prod * (n + 1); 47 f[0] = 1; 48 for (int j = 0; j < n; j++) 49 for (int i = 1; i <= m; i++) 50 if (a[j] <= i) 51 f[i] = add(f[i - a[j]], f[i]); 52 for (int i = 1; i <= m; i++) 53 f[i] = add(f[i], f[i - 1]); 54 } 55 56 int Lagrange(ll _x) { 57 if (_x <= m) 58 return f[_x]; 59 int k = _x % prod; 60 int x = (_x / prod) % Mod; 61 int rt = 0; 62 for (int i = 0; i <= n; i++) { 63 int tmp = f[i * prod + k]; 64 for (int j = 0; j <= n; j++) 65 if (i ^ j) 66 tmp = mul(tmp, mul(sub(x, j), inv(sub(i, j), Mod))); 67 rt = add(rt, tmp); 68 } 69 return rt; 70 } 71 72 ll l, r; 73 inline void solve() { 74 scanf("%lld%lld", &l, &r); 75 printf("%d\n", sub(Lagrange(r), Lagrange(l - 1))); 76 } 77 78 int main() { 79 init(); 80 solve(); 81 return 0; 82 }
Problem C 解决npc
题目大意
要求构造一个点数不超过$50$,边数不超过$100$的有向图,使得它的本质不同的拓扑序的个数为$x$。
当$x = 1,2$的时候特判。
当$x$不大的时候,构造一条链和一个点就行了。
当$x$比较大的时候,考虑这样一个东西:
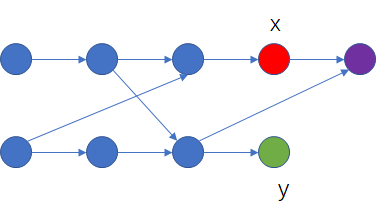
考虑在加入紫色节点前,以红色节点结尾的拓扑序的个数为$x$,以绿色节点结尾的拓扑序的个数为$y$,如图所示加入紫色节点,那么不难得到以紫色节点为结尾的拓扑序有$x + y$个。
那么就可以直接爆搜了。
Code

1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 #include <vector> 5 using namespace std; 6 typedef bool boolean; 7 8 #define pii pair<int, int> 9 10 const int Lim = 50; 11 12 int X; 13 14 inline void init() { 15 scanf("%d", &X); 16 } 17 18 int type[Lim + 5]; 19 vector<pii> E; 20 void dfs(int x, int y, int d, int lim) { 21 if (d == lim || d == Lim || x + y > X) 22 return; 23 if (x + y == X) { 24 vector<int> L(2), R(2); 25 L[0] = 0, L[1] = 1, R[0] = 2, R[1] = 3; 26 E.push_back(pii(0, 1)); 27 E.push_back(pii(2, 3)); 28 E.push_back(pii(0, 3)); 29 for (int i = 4; i < d; i++) 30 if (!type[i]) { 31 E.push_back(pii(L.back(), i)); 32 E.push_back(pii(R[R.size() - 2], i)); 33 L.push_back(i); 34 } else { 35 E.push_back(pii(R.back(), i)); 36 E.push_back(pii(L[L.size() - 2], i)); 37 R.push_back(i); 38 } 39 40 printf("%d %d\n", d, (signed) E.size()); 41 for (int i = 0; i < (signed) E.size(); i++) 42 printf("%d %d\n", E[i].first, E[i].second); 43 exit(0); 44 } 45 46 type[d] = 0; 47 dfs(x + y, y, d + 1, lim); 48 type[d] = 1; 49 dfs(x, x + y, d + 1, lim); 50 } 51 52 inline void solve() { 53 if (X == 1) { 54 printf("2 1\n0 1\n"); 55 } else if (X == 2) { 56 printf("3 2\n0 1\n2 1\n"); 57 }else if (X <= 40) { 58 printf("%d %d\n", X, X - 2); 59 for (int i = 0; i < X - 2; i++) 60 printf("%d %d\n", i, i + 1); 61 } else { 62 for (int lim = 7; lim <= 50; lim++) 63 dfs(2, 3, 4, lim); 64 puts("Failed"); 65 } 66 } 67 68 int main() { 69 init(); 70 solve(); 71 return 0; 72 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号