NOIP 2024 简要题解
从这里开始
啥?你问我为啥没事做个 noip?这是工作一部分(摊手手)
Problem A 编辑字符串
两个都不能动的字符直接判断。其中一个能动的话,优先进行匹配。如果它不在最优解中匹配,那么显然可以通过调整使得它能匹配上,同时总匹配数不变。
剩下从左到右依次考虑两个串中都能动的字符。如果能在 $i$ 处匹配那么就在 $i$ 处匹配。原因类似于上面,反正总可以拆一个匹配来满足 $i$ 处的匹配。
然后就是匹配 0,还是匹配 1 的问题。但其实这个是无所谓的,不妨我们设能匹配 0 的时候优先匹配 0。因为如果两个颜色都剩了,那么 0 和 1 的数量和是刚好等于当前连通块和另一个串前一个相交的和后一个相交的重叠的部分的长度($x + y = u + v$),并且同时有 $a + b = u$(不然前面的连通块至少有一个颜色被耗完)。(假设中间没有多余的连通块)
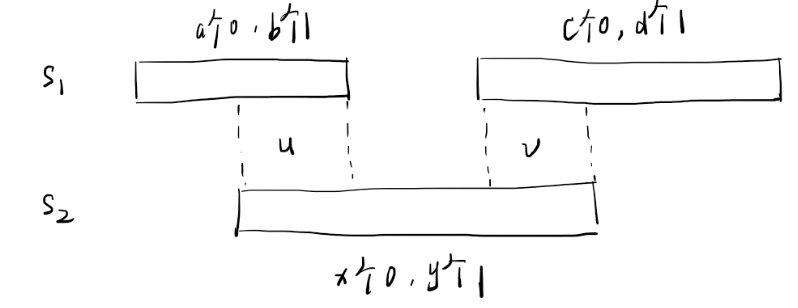
- 如果在 $u$ 这一部分,有一个 $s_1$ 中的 0 没有被匹配,那么 $v$ 中会多一个 $0$。拆一对 $0$ 拿过来,匹配数不变,但是满足我们分配的规则。
- 如果在 $v$ 这一部分,显然填 0 还是填 1 都是无所谓的。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
#define pii pair<int, int>
int T, n;
char sa[N], sb[N];
char ta[N], tb[N];
int sid_a[N], sid_b[N];
vector<pii> segments;
void label(int& seg_cnt, char* s, char* t, int* sid) {
for (int i = 0; i < n; i++) {
if (i == 0 || (t[i - 1] == '0' && t[i] == '1')) {
seg_cnt++;
segments.emplace_back(0, 0);
}
if (t[i] == '1') {
sid[i] = seg_cnt - 1;
if (s[i] == '0') {
segments.back().first++;
} else {
segments.back().second++;
}
} else {
sid[i] = -1;
}
}
}
bool check(int pos, int* sid, char col) {
auto& seg = segments[sid[pos]];
auto& rest = (col == '0' ? seg.first : seg.second);
if (rest) {
--rest;
return true;
}
return false;
}
int collect(pii& a, pii& b) {
if (a.first && b.first) {
--a.first, --b.first;
return true;
}
if (a.second && b.second) {
--a.second, --b.second;
return true;
}
return false;
}
void solve() {
scanf("%d", &n);
scanf("%s", sa);
scanf("%s", sb);
scanf("%s", ta);
scanf("%s", tb);
int seg_cnt = 0;
label(seg_cnt, sa, ta, sid_a);
label(seg_cnt, sb, tb, sid_b);
int ans = 0;
for (int i = 0; i < n; i++) {
if (ta[i] == '0' && tb[i] == '0') {
ans += sa[i] == sb[i];
} else if (ta[i] == '0') {
ans += check(i, sid_b, sa[i]);
} else if (tb[i] == '0') {
ans += check(i, sid_a, sb[i]);
}
}
for (int i = 0; i < n; i++) {
if (ta[i] == '1' && tb[i] == '1') {
ans += collect(segments[sid_a[i]], segments[sid_b[i]]);
}
}
segments.clear();
printf("%d\n", ans);
}
int main() {
scanf("%d", &T);
while (T--) {
solve();
}
return 0;
}
Problem B 遗失的赋值
容易注意到,对于值未确定的 $x_i$,施加在 $x_i$ 和 $x_{i + 1}$ 上的限制一定可以让其不生效。
设 $f_{i, 0/1}$ 表示考虑了前 $i-1$ 个限制, $x_i$ 的值是否是确定的,此时的方案数。
- 当转移到一个非确定的 $x$ 时,转移矩阵如下:
$$
\left ( \begin{matrix}
v^2 & 0 \\
v(v-1) & v
\end{matrix} \right )
$$ - 当转移到一个确定的 $x$ 时,由于 $f_{i, 0} = 0$,只需要确定一下 $f_{i, 1}$。容易得到 $f_{i, 1} = f_{i-1, 0} v^2 + f_{i - 1, 1}(v(v-1) + 1)$
对于前一部分简单推一下式子可以得到,$L$ 个矩阵相乘的结果为:
$$
\left ( \begin{matrix}
v^{2L} & 0 \\
v^L(v^L-1) & v^L
\end{matrix} \right )
$$
从一个确定的 $x_i$ 转移到另一个确定的 $x_j$,首先通过第一种转移走 $j - i - 1$ 步,再通过第二种转移走 1 步。
对于答案为 0 的情况需要特判。
Code
#include <bits/stdc++.h>
using namespace std;
class Input {
public:
} in;
#define _isdigit(_x) ((_x) >= '0' && (_x) <= '9')
Input& operator >> (Input& in, int& x) {
char u;
while (~(u = getchar()) && !_isdigit(u));
for (x = u - '0'; ~(u = getchar()) && _isdigit(u); x = x * 10 + u - '0');
return in;
}
#define ll long long
const int Mod = 1e9 + 7;
class Zi {
public:
int v;
Zi(int v = 0) : v(v) { }
Zi(ll x) : v(x % Mod) { }
friend Zi operator + (Zi a, Zi b) {
int x = a.v + b.v;
return (x >= Mod) ? (x - Mod) : x;
}
friend Zi operator - (Zi a, Zi b) {
int x = a.v - b.v;
return (x < 0) ? (x + Mod) : x;
}
friend Zi operator * (Zi a, Zi b) {
return 1ll * a.v * b.v;
}
};
Zi qpow(Zi a, int p) {
Zi rt = 1;
for ( ; p; p >>= 1, a = a * a) {
if (p & 1) {
rt = rt * a;
}
}
return rt;
}
int T;
int n, m, v;
vector<pair<int, int>> raw_input;
vector<int> a;
void solve() {
raw_input.clear();
a.clear();
in >> n >> m >> v;
for (int i = 1, c, d; i <= m; i++) {
in >> c >> d;
raw_input.emplace_back(c, d);
}
sort(raw_input.begin(), raw_input.end());
for (int i = 1; i < m; i++) {
if (raw_input[i].first == raw_input[i - 1].first && raw_input[i].second != raw_input[i - 1].second) {
puts("0");
return;
}
}
for (int i = 0; i < m; i++) {
if (!i || raw_input[i].first != raw_input[i - 1].first) {
a.push_back(raw_input[i].first);
}
}
Zi v2 = Zi(v) * v, v3 = Zi(v) * (v - 1);
Zi f0 = 0, f1 = qpow(v2, a[0] - 1), g0, g1;
for (int i = 1; i < (signed) a.size(); i++) {
int L = a[i] - a[i - 1];
if (L == 1) {
g0 = 0;
g1 = f0 * v2 + f1 * (v3 + 1);
} else {
// (L - 1) steps
auto vL = qpow(v, L - 1);
g0 = f0 * qpow(v2, L - 1) + f1 * vL * (vL - 1);
g1 = f1 * vL;
f0 = g0, f1 = g1;
g0 = 0;
g1 = f0 * v2 + f1 * (v3 + 1);
}
f0 = g0, f1 = g1;
}
int an = a.back();
Zi ans = (f0 + f1) * qpow(v2, n - an);
printf("%d\n", ans.v);
}
int main() {
in >> T;
while (T--) {
solve();
}
return 0;
}
Problem C 树的遍历
先考虑 $k = 1$ 的情况,我们将边视为一个点,在原树上有公共点的边在新图上有边相连。题目问的是在这个新图的上的 dfs 生成树。
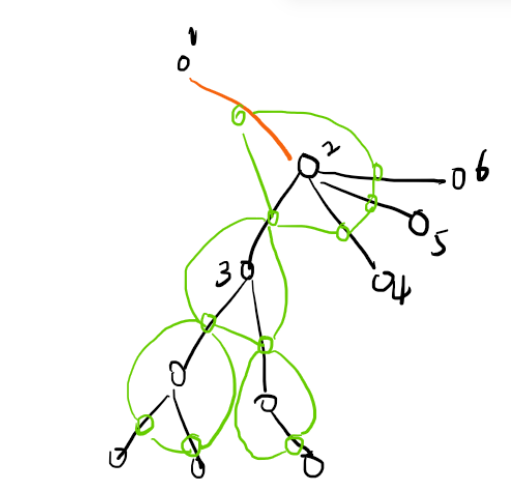
假设从橘色边开始,加入先选择了遍历和 $2$ 相邻的点的边,假如接下来是 $(2, 3)$,那么需要把剩下所有和 2 相连的边全部遍历完才能从 $(2, 3)$ 回溯。最终与 $2$ 相邻的边在 dfs 生成树上会构成一条链。
可以观察到对于每个点,都可以为与它相邻的边选择它们最终构成的链的顺序,除了要求距离根最近的一条边必须为环上第一个点。
因此方案数为 $\prod_p (d_p - 1) !$
我们接着考虑怎么判定一棵生成树能否由某一条边生成。容易想到我们只需要所有点,每个点在分配周围的边的顺序的时候,将离根最近的一条边作为第一条边。
容易把这个结论拓展到某个边集,要求生成树能被边集中任意一条边生成。考虑两条边的情况下,要求这两条边的链上每条边在端点的环中被选择为第一个或者最后一个。因此如果边集在一条链上,那么方案数为 $\prod_p (d_p - 1 - [p 在链内部])!$
剩下的问题很简单了,考虑容斥。硬点一个边集要求这个边集中每个边都能以它为根得到生成树,计算这样的生成树的数量,容斥系数为 $(-1)^{边集大小 - 1}$。
这个直接树形 dp 即可。每个点有 3 种状态,当前不处于链上,当前处于链中间,子树内存在完整的链。转移的时候有一个小细节,如果当前点为链中间,当前点最后乘上的系数为 $(deg - 2)!$。在特殊边的时候决策这条边是否被硬点,硬点需要乘上系数 $-1$。
Code
#include <bits/stdc++.h>
using namespace std;
class Input {
public:
} in;
#define _isdigit(_x) ((_x) >= '0' && (_x) <= '9')
Input& operator >> (Input& in, int& x) {
char u;
while (~(u = getchar()) && !_isdigit(u));
for (x = u - '0'; ~(u = getchar()) && _isdigit(u); x = x * 10 + u - '0');
return in;
}
#define ll long long
const int Mod = 1e9 + 7;
class Zi {
public:
int v;
Zi(int v = 0) : v(v) { }
Zi(ll x) : v(x % Mod) { }
friend Zi operator - (Zi a) {
return Zi(0) - a;
}
friend Zi operator + (Zi a, Zi b) {
int x = a.v + b.v;
return (x >= Mod) ? (x - Mod) : x;
}
friend Zi operator - (Zi a, Zi b) {
int x = a.v - b.v;
return (x < 0) ? (x + Mod) : x;
}
friend Zi operator * (Zi a, Zi b) {
return 1ll * a.v * b.v;
}
};
Zi qpow(Zi a, int p) {
Zi rt = 1;
for ( ; p; p >>= 1, a = a * a) {
if (p & 1) {
rt = rt * a;
}
}
return rt;
}
const int N = 1e5 + 5;
int n, K;
bool is_selected[N];
vector<pair<int, int>> G[N];
Zi fac[N];
Zi f[N], g[N], h[N];
void dfs(int p, int fa, bool special) {
f[p] = 1, g[p] = 0, h[p] = 0;
Zi newh = 0;
for (auto [e, id] : G[p]) {
if (e == fa) {
continue;
}
dfs(e, p, is_selected[id]);
Zi nf = f[p] * f[e];
Zi ng = f[p] * g[e] + g[p] * f[e];
Zi nh = f[p] * h[e] + h[p] * f[e];
newh = newh * f[e] + g[p] * g[e];
f[p] = nf, g[p] = ng, h[p] = nh;
}
int deg = G[p].size();
f[p] = f[p] * fac[deg - 1];
if (deg >= 2) {
g[p] = g[p] * fac[deg - 2];
newh = newh * fac[deg - 2];
} else {
g[p] = 0;
newh = 0;
}
h[p] = h[p] * fac[deg - 1] + newh;
if (special) {
h[p] = h[p] - f[p] - g[p];
g[p] = -f[p];
}
}
void solve() {
in >> n >> K;
fac[0] = fac[1] = 1;
for (int i = 2; i <= n; i++) {
fac[i] = fac[i - 1] * i;
}
for (int i = 1, u, v; i < n; i++) {
in >> u >> v;
G[u].emplace_back(v, i);
G[v].emplace_back(u, i);
}
for (int i = 1, x; i <= K; i++) {
in >> x;
is_selected[x] = true;
}
dfs(1, 0, false);
Zi ans = -h[1];
printf("%d\n", ans.v);
fill(is_selected, is_selected + n + 1, false);
for (int i = 1; i <= n; i++) {
G[i].clear();
}
}
int main() {
int _, T;
in >> _ >> T;
while (T--) {
solve();
}
return 0;
}
Problem D 树上查询
考虑 $m$ 个点的 lca 的等于相邻两个点的 lca 的深度最低的一个。证明考虑 $m$ 点的 $lca$ 一定存在两个点在它的不同子树,从一边刚走到另一边时这对点的 lca 即是所求。
问题其实等价于给一个长度为 $n - 1$ 的序列,每次询问一个区间中任意长度大于等于 $k - 1$ 连续子区间的最小值最大能有多少。(需要特判 $k=1$ 的时候)
整体二分即可获得一个 $O(n\log^2 n )$ 的做法。
考虑把这些数从大到小加入进来,每加入一个数会获得一个区间,$([l', r'], d)$,$[l', r’]$ 是此时与之连通的数的区间,$d$ 是当前这个数的值,也就是这段数的最小值。显然总共有 $O(n)$ 个区间。
那么对于每个询问相当于是询问所有和 $[l, r-1]$ 的交超过长度超过 $k - 1$ 的区间,它的 $d$ 的最大值有多少。为了简洁,我们下面不再考虑这几个 $-1$ 的问题。(你也可以将上面的区间改成 $[1, n]$,初始再加入 $1, 2, \cdots, n$ 来不考虑这个边界问题)
条件等价于 $\min(r', r) - \max(l', l) + 1\geqslant k$。讨论 $l', l$ 的大小。
- 如果 $l' > l$,那么有 $\min(r', r) - l' + 1 \geqslant k$。有 $r' - l' \geqslant k - 1, r-l' \geqslant k - 1$
所以有 $l <l' \leqslant r-k+1$,同时有 $r' - l' \geqslant k - 1$。按区间长度以及 $k$ 这一维扫描线即可,用线段树维护区间最大值。 - 如果 $l' \leqslant l$,那么有 $\min(r', r) - l + 1 \geqslant k$,$r$ 显然是满足的,那么有 $r' - l + 1 \geqslant k$,即 $r' \geqslant l+k-1$。
按 $l$ 扫描线,用线段树维护区间最大值即可。
总时间复杂度 $O((n+q)\log n)$
Code


 浙公网安备 33010602011771号
浙公网安备 33010602011771号