蓝书3.2 最短路

T1 银牛派对 luogu 1821

题目大意：

一个有向图

求任意节点到定点的最短距离+定点到该点的最短距离之和的最大值

思路：

正反dij

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<vector>
 8 #include<queue>
 9 #define inf 2139062143
10 #define ll long long
11 #define MAXN 100100
12 #define eps 1e-5
13 using namespace std;
14 inline int read()
15 {
16     int x=0,f=1;char ch=getchar();
17     while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
18     while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
19     return x*f;
20 }
21 int ans,n,m,s,dis[MAXN],vis[MAXN],Dis[MAXN],Vis[MAXN];
22 int to[MAXN],nxt[MAXN],val[MAXN],fst[MAXN],cnt;
23 int To[MAXN],Nxt[MAXN],Val[MAXN],Fst[MAXN],Cnt;
24 void add(int u,int v,int w) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v,val[cnt]=w;}
25 void Add(int u,int v,int w) {Nxt[++Cnt]=Fst[u],Fst[u]=Cnt,To[Cnt]=v,Val[Cnt]=w;}
26 struct node
27 {
28     int id,val;
29     bool operator < (const node &a) const
30     {
31         return val>a.val;
32     }
33 };
34 priority_queue <node> q,Q;
35 void dij()
36 {
37     memset(dis,127,sizeof(dis));
38     dis[s]=0;q.push((node){s,0});int x;
39     while(!q.empty())
40     {
41         x=q.top().id;q.pop();
42         if(vis[x]) continue;vis[x]=1;
43         for(int i=fst[x];i;i=nxt[i])
44             if(dis[to[i]]>dis[x]+val[i]) {dis[to[i]]=dis[x]+val[i];q.push((node){to[i],dis[to[i]]});}
45     }
46 }
47 void Dij()
48 {
49     memset(Dis,127,sizeof(Dis));
50     Dis[s]=0;Q.push((node){s,0});int x;
51     while(!Q.empty())
52     {
53         x=Q.top().id;Q.pop();
54         if(Vis[x]) continue;Vis[x]=1;
55         for(int i=Fst[x];i;i=Nxt[i])
56             if(Dis[To[i]]>Dis[x]+Val[i]) {Dis[To[i]]=Dis[x]+Val[i];Q.push((node){To[i],Dis[To[i]]});}
57     }
58 }
59 int main()
60 {
61     n=read(),m=read(),s=read();int a,b,c;
62     while(m--) {a=read(),b=read(),c=read();add(a,b,c);Add(b,a,c);}
63     dij();Dij();
64     for(int i=1;i<=n;i++)
65         if(i!=s&&dis[i]!=inf&&Dis[i]!=inf) ans=max(ans,dis[i]+Dis[i]);
66     printf("%d",ans);
67 }

View Code

T2 Roadblocks poj 3255

题目大意：

求次短路

思路：

开一个dis的同时开一个次短路数组

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<vector>
 8 #include<queue>
 9 #define inf 2139062143
10 #define ll long long
11 #define MAXN 100100
12 #define eps 1e-5
13 using namespace std;
14 inline int read()
15 {
16     int x=0,f=1;char ch=getchar();
17     while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
18     while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
19     return x*f;
20 }
21 int n,m,dis[MAXN],subdis[MAXN],vis[MAXN],q[MAXN<<1],l=1,r;
22 int to[MAXN<<1],nxt[MAXN<<1],val[MAXN<<1],fst[MAXN],cnt;
23 void add(int u,int v,int w) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v,val[cnt]=w;}
24 void spfa()
25 {
26     memset(dis,127,sizeof(dis));
27     memset(subdis,127,sizeof(subdis));
28     q[++r]=1,dis[1]=0,vis[1]=1;
29     while(l<=r)
30     {
31         int x=q[l++];vis[x]=0;
32         for(int i=fst[x];i;i=nxt[i])
33         {
34             if(dis[to[i]]>dis[x]+val[i])
35             {
36                 subdis[to[i]]=dis[to[i]],dis[to[i]]=dis[x]+val[i];
37                 if(!vis[to[i]]) vis[to[i]]=1,q[++r]=to[i];
38             }
39             if(subdis[to[i]]>subdis[x]+val[i])
40             {
41                 subdis[to[i]]=subdis[x]+val[i];
42                 if(!vis[to[i]]) vis[to[i]]=1,q[++r]=to[i];
43             }
44             if(dis[to[i]]<dis[x]+val[i]&&subdis[to[i]]>dis[x]+val[i])
45             {
46                 subdis[to[i]]=dis[x]+val[i];
47                 if(!vis[to[i]]) vis[to[i]]=1,q[++r]=to[i];
48             }
49         }
50     }
51 }
52 int main()
53 {
54     n=read(),m=read();int a,b,c;
55     while(m--){a=read(),b=read(),c=read();add(a,b,c);add(b,a,c);}
56     spfa();printf("%d",subdis[n]);
57 }

View Code

T3 最短路计数 luogu 1144

题目大意：

求有多少种最短路

思路：

spfa的同时记录有多少种情况

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<vector>
 8 #include<queue>
 9 #define inf 2139062143
10 #define ll long long
11 #define MAXN 1001000
12 #define MOD 100003
13 using namespace std;
14 inline int read()
15 {
16     int x=0,f=1;char ch=getchar();
17     while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
18     while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
19     return x*f;
20 }
21 int n,m,dis[MAXN],vis[MAXN],q[MAXN],l,r,ans[MAXN];
22 int to[MAXN<<2],nxt[MAXN<<2],fst[MAXN],cnt;
23 void add(int u,int v) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v;}
24 void spfa()
25 {
26     memset(dis,127,sizeof(dis));
27     q[++r]=1,dis[1]=0,ans[1]=vis[1]=1;
28     while(l<=r)
29     {
30         int x=q[l++];
31         for(int i=fst[x];i;i=nxt[i])
32             if(dis[to[i]]==dis[x]+1) (ans[to[i]]+=ans[x])%=MOD;
33             else if(dis[to[i]]>dis[x]+1)
34             {
35                 ans[to[i]]=ans[x],dis[to[i]]=dis[x]+1;
36                 if(!vis[to[i]]) vis[to[i]]=1,q[++r]=to[i];
37             }
38         vis[x]=0;
39     }
40 }
41 int main()
42 {
43     n=read(),m=read();int a,b,c;
44     while(m--){a=read(),b=read();add(a,b);add(b,a);}
45     spfa();
46     for(int i=1;i<=n;i++)printf("%d\n",ans[i]);
47 }

View Code

T4 最优贸易 luogu 1073

题目大意：

一个有向图在一条路径上可以在一个点以该点的价格买入商品在该点之后在另一个点卖出求最大利润

思路：

dfs居然就过了

dfs的同时维护经过的最小值并对每个点维护一个dp值记录利润

每当一个点经过的最小值与dp值不被更新时就可以结束dfs了

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<vector>
 8 #include<queue>
 9 #define inf 2139062143
10 #define ll long long
11 #define MAXN 1001000
12 #define MOD 100003
13 using namespace std;
14 inline int read()
15 {
16     int x=0,f=1;char ch=getchar();
17     while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
18     while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
19     return x*f;
20 }
21 int n,m,dp[MAXN],mn[MAXN],g[MAXN];
22 int to[MAXN<<2],nxt[MAXN<<2],fst[MAXN],cnt;
23 void add(int u,int v) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v;}
24 void dfs(int x,int mnx,int las)
25 {
26     int fl=1;
27     mnx=min(g[x],mnx);
28     if(mn[x]>mnx) mn[x]=mnx,fl=0;
29     if(max(dp[las],g[x]-mnx)>dp[x]) dp[x]=max(dp[las],g[x]-mnx),fl=0;
30     if(fl) return;
31     for(int i=fst[x];i;i=nxt[i]) dfs(to[i],mnx,x);
32 }
33 
34 int main()
35 {
36     n=read(),m=read();int a,b,c;
37     for(int i=1;i<=n;i++) g[i]=read();
38     memset(mn,127,sizeof(mn));
39     for(int i=1;i<=m;i++){a=read(),b=read(),c=read();add(a,b);if(c==2) add(b,a);}
40     dfs(1,inf,0);
41     printf("%d\n",dp[n]);
42 }

View Code

T5 汽车加油行驶 luogu 4009

题目大意：

给定一个

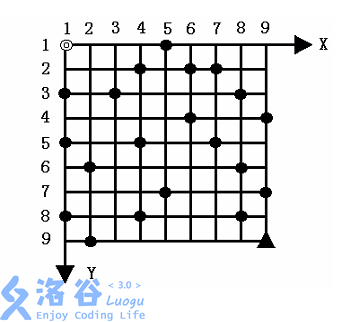
一辆汽车从起点◎出发驶向右下角终点▲，其坐标为

在若干个网格交叉点处，设置了油库，可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则

汽车只能沿网格边行驶，装满油后能行驶
汽车经过一条网格边时，若其
汽车在行驶过程中遇油库则应加满油并付加油费用
在需要时可在网格点处增设油库，并付增设油库费用

求所付费用最少的行驶路线所需的费用

思路：

因为K非常小可以把图分层

第L张图的i j 表示该车行驶到i j还剩L单位的油所需的最小代价

由于在加油站强制消费

则若一个点为加油站可以从i j l (0<=l<k)向i j K连一条长度为A 的边

i j K向i+-1 j+-1 K-1连长度为0/B的边

若不是加油站可以从i j l(0<=l<k)向i j K连一条长度为A+C的边

i j l(0<l<=K)向i+-1 j+-1 l-1连长度为0/B的边

跑完最短路之后在K+1个图中找到终点的dis中最小的

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<vector>
 8 #include<queue>
 9 #define inf 2139062143
10 #define ll long long
11 #define MAXN 200100
12 #define eps 1e-5
13 using namespace std;
14 inline int read()
15 {
16     int x=0,f=1;char ch=getchar();
17     while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
18     while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
19     return x*f;
20 }
21 int n,k,a,b,c,dis[MAXN],vis[MAXN],q[MAXN<<1],l=1,r;
22 int to[MAXN<<2],nxt[MAXN<<2],fst[MAXN<<2],val[MAXN<<2],cnt,ans;
23 void add(int u,int v,int w) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v,val[cnt]=w;}
24 int calc(int l,int i,int j) {return l*n*n+i*n+j;}
25 void spfa()
26 { 
27     memset(dis,127,sizeof(dis));
28     q[++r]=k*n*n,dis[k*n*n]=0,vis[k*n*n]=1;
29     while(l<=r)
30     {
31         int x=q[l++];vis[x]=0;
32         for(int i=fst[x];i;i=nxt[i])
33             if(dis[to[i]]>dis[x]+val[i])
34             {
35                 dis[to[i]]=dis[x]+val[i];
36                 if(!vis[to[i]]) vis[to[i]]=1,q[++r]=to[i];
37             }
38     }
39 }
40 int main()
41 {
42     n=read(),k=read(),a=read(),b=read(),c=read();int x;
43     for(int i=0;i<n;i++)
44         for(int j=0;j<n;j++) 
45         {
46             x=read();
47             if(x||(!i&&!j)) 
48             {
49                 for(int l=0;l<k;l++) add(calc(l,i,j),calc(k,i,j),a);
50                 if(j<n-1) add(calc(k,i,j),calc(k-1,i,j+1),0);
51                 if(i<n-1) add(calc(k,i,j),calc(k-1,i+1,j),0);
52                 if(j) add(calc(k,i,j),calc(k-1,i,j-1),b);
53                 if(i) add(calc(k,i,j),calc(k-1,i-1,j),b);
54             }
55             else
56             {
57                 for(int l=0;l<k;l++) add(calc(l,i,j),calc(k,i,j),a+c);
58                 for(int l=1;l<=k;l++)
59                 {
60                     if(j<n-1) add(calc(l,i,j),calc(l-1,i,j+1),0);
61                     if(i<n-1) add(calc(l,i,j),calc(l-1,i+1,j),0);
62                     if(j) add(calc(l,i,j),calc(l-1,i,j-1),b);
63                     if(i) add(calc(l,i,j),calc(l-1,i-1,j),b);
64                 }
65             }
66         }
67     spfa();ans=inf;
68     for(int i=0;i<=k;i++) ans=min(ans,dis[calc(i,n-1,n-1)]);
69     printf("%d",ans);
70 }

View Code

T6 道路与航线 bzoj 2200

题目大意：

图中有无向边和有向边只有有向边边权可能为负且有向边不在任何一个环内求单源最短路

思路：

好像直接用spfa+slf就过了但还是正经的做一下

如果把所有无向边用并查集缩起来之后有向边连接成一个拓扑图

所以对每个联通块内部使用dij处理跑多源最短路

按照拓扑的方法搞

（开了O2的vector跑的飞快数组反而爆炸了

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<cstdlib>
 5 #include<cstring>
 6 #include<algorithm>
 7 #include<vector>
 8 #include<queue>
 9 #define inf 1061109567
10 #define ll long long
11 #define MAXN 50100
12 #define eps 1e-5
13 using namespace std;
14 inline int read()
15 {
16     int x=0,f=1;char ch=getchar();
17     while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
18     while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
19     return x*f;
20 }
21 int n,st,m1,m2,dis[MAXN],vis[MAXN],fa[MAXN],q[MAXN],l=1,r;
22 int to[MAXN<<1],nxt[MAXN<<1],val[MAXN<<1],fst[MAXN],cnt;
23 int To[MAXN],Nxt[MAXN],Val[MAXN],Fst[MAXN],Cnt,Ind[MAXN],s[MAXN],t[MAXN];
24 vector <int> vec[MAXN];
25 int find(int x) {return x==fa[x]?x:fa[x]=find(fa[x]);}
26 void add(int u,int v,int w) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v,val[cnt]=w;}
27 void Add(int u,int v,int w) {Nxt[++Cnt]=Fst[u],Fst[u]=Cnt,To[Cnt]=v,Val[Cnt]=w,Ind[v]++;}
28 void merge(int a,int b) {int f1=find(a),f2=find(b);if(f1!=f2) fa[f1]=f2;}
29 struct node
30 {
31     int id,val;
32     bool operator < (const node &a) const
33     {
34         return val>a.val;
35     }
36 };
37 int main()
38 {
39     n=read(),m1=read(),m2=read(),st=read();int a,b,c;
40     for(int i=1;i<=n;i++) fa[i]=i;
41     for(int i=1;i<=m1;i++) {a=read(),b=read(),c=read();add(a,b,c);add(b,a,c);merge(a,b);}
42     for(int i=1;i<=m2;i++) {s[i]=a=read(),t[i]=b=read(),c=read();Add(find(a),find(b),c);}
43     for(int i=1;i<=n;i++) if(find(i)==i&&!Ind[i]) {q[++r]=i;vec[i].push_back(i);}
44     memset(dis,127,sizeof(dis));
45     dis[st]=0;vec[find(st)].push_back(st);
46     while(l<=r)
47     {
48         a=q[l++];priority_queue <node> que;
49         for(int i=0;i<vec[a].size();i++)
50             que.push((node){vec[a][i],dis[vec[a][i]]});
51         while(!que.empty())
52         {
53             b=que.top().id;que.pop();
54             if(vis[b]) continue;vis[b]=1;
55             for(int i=fst[b];i;i=nxt[i])
56                 if(dis[to[i]]>dis[b]+val[i]) {dis[to[i]]=dis[b]+val[i];que.push((node){to[i],dis[to[i]]});}
57         }
58         for(int i=Fst[a];i;i=Nxt[i])
59         {
60             Ind[To[i]]--;vec[To[i]].push_back(t[i]);dis[t[i]]=min(dis[t[i]],dis[s[i]]+Val[i]);
61             if(!Ind[To[i]]) q[++r]=To[i];
62         }
63     }
64     for(int i=1;i<=n;i++)
65         if(dis[i]>=inf) puts("NO PATH");
66         else printf("%d\n",dis[i]);
67 }

View Code

posted @ 2018-07-24 12:57 jack_yyc 阅读(246) 评论(0) 编辑收藏举报

刷新页面返回顶部

jack_yyc

蒟蒻

蓝书3.2 最短路

公告