2021ccpc预选重赛
F
\(dp\)出前\(i\)个位置匹配了多少个\(nunhehheh\),再统计每个位置后面\(a\)的个数即可计算答案
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 100100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
namespace CALC
{
inline int pls(int a,int b){return a+b>=MOD?a+b-MOD:(a+b<0?a+b+MOD:a+b);}
inline int mns(int a,int b){return a-b<0?a-b+MOD:(a-b>=MOD?a-b-MOD:a-b);}
inline int mul(int a,int b){return (1LL*a*b)%MOD;}
inline void inc(int &a,int b){a=pls(a,b);}
inline void dec(int &a,int b){a=mns(a,b);}
inline void tms(int &a,int b){a=mul(a,b);}
inline int qp(int x,int t,int res=1)
{for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(res,x);return res;}
inline int Inv(int x){return qp(x,MOD-2);}
}
using namespace CALC;
int n,pw[MAXN],f[MAXN][10],sum[10],numa[MAXN],ans;
char s[MAXN];
int main()
{
pw[0]=1;rep(i,1,1e5) pw[i]=mul(pw[i-1],2);
rep(T,1,read())
{
scanf("%s",s+1);n=strlen(s+1);
numa[n+1]=0;ans=0;Fill(sum,0);
dwn(i,n,1) numa[i]=numa[i+1]+(s[i]=='a');
rep(i,1,n)
{
Fill(f[i],0);
if(s[i]=='n') f[i][0]=1,f[i][2]=sum[1];
else if(s[i]=='u') f[i][1]=sum[0];
else if(s[i]=='h')
f[i][3]=sum[2],f[i][5]=sum[4],f[i][6]=sum[5],f[i][8]=sum[7];
else if(s[i]=='e') f[i][4]=sum[3],f[i][7]=sum[6];
rep(j,0,8) inc(sum[j],f[i][j]);
inc(ans,mul(f[i][8],mns(pw[numa[i+1]],1)));
}
printf("%d\n",ans);
}
}
H
对于一个\(m\)的排列,分两类情况讨论
1.当这个排列完全属于一个\(n\)的排列时,容易得到此时贡献为\(m!(n-m+1)!\)
2.否则该排列被分成两个部分,分别存在于两个相邻的排列中
先不考虑排列数加一造成的影响,则此时贡献为\((m-1)m!(n-m)!\)
和上式加和可得\(n\cdot m!(n-m)!\),即\(m\)的排列可以放在任意位置,超出去的部分放到\(n\)个位置的前面
由于这种情况要求两个相邻的\(n\)排列的前面一部分一样
将该\(n\)排列分为三部分\(a\ b\ c\),其中\(a\ c\)中的所有数均\(\le m\),\(b\)中的数\(>m\)
容易发现当且仅当\(b\ c\)部分为一个单调下降序列时,这个排列的下一个排列前面才不会是\(a\)部分,否则均满足条件
考虑枚举\(c\)的长度,则前面\(a\)的部分随意排列,
不合法情况总数为:\(\sum\limits_{i=1}^{m-1}\binom{m}{i}(m-i)!=\sum\limits_{i=1}^{m-1}\frac{m!}{i!}=m!\sum\limits_{i=1}^{m-1}\frac{1}{i!}\)
最终答案为\(m!(n(n-m)!-\sum\limits_{i=1}^{m-1}\frac{1}{i!})\)
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 1001001
#define MOD 1000000007
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
namespace CALC
{
inline int pls(int a,int b){return a+b>=MOD?a+b-MOD:(a+b<0?a+b+MOD:a+b);}
inline int mns(int a,int b){return a-b<0?a-b+MOD:(a-b>=MOD?a-b-MOD:a-b);}
inline int mul(int a,int b){return (1LL*a*b)%MOD;}
inline void inc(int &a,int b){a=pls(a,b);}
inline void dec(int &a,int b){a=mns(a,b);}
inline void tms(int &a,int b){a=mul(a,b);}
inline int qp(int x,int t,int res=1)
{for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(res,x);return res;}
inline int Inv(int x){return qp(x,MOD-2);}
}
using namespace CALC;
int n,m,fac[MAXN],ifac[MAXN],sum[MAXN];
void init(int n=1e6)
{
fac[0]=ifac[0]=1;rep(i,1,n) fac[i]=mul(fac[i-1],i);
ifac[n]=Inv(fac[n]);dwn(i,n-1,1) ifac[i]=mul(ifac[i+1],i+1);
rep(i,1,n) sum[i]=pls(sum[i-1],ifac[i]);
}
int main()
{
init();rep(T,1,read())
{
n=read(),m=read();
printf("%d\n",mul(fac[m],mns(mul(fac[n-m],n),sum[m-1])));
}
}
I
容易想到直接将边拆成点,但直接做显然复杂度无法接受
将所有边同一起点的边按照\(a_e\)升序排列之后,每条边可以优化的边即在一段连续的区间内
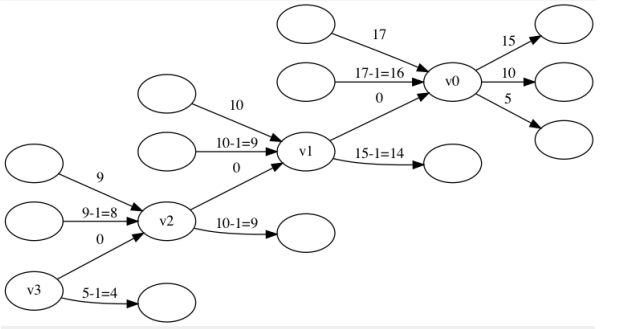
如图所示,将每个点\(x\)拆成\(deg_x+1\)个点,所有边权为\(a_e\)边起点仍为\(x\),边权为\(a_e-b_e\)的边按\(a_e\)排序后起点不同,相邻的边起点直接升序连接0边
对于终点为\(v\)的边,二分出合法区间,然后将\(a_e\)与\(a_e-b_e\)的边均连向\(a\)最小的点即可 正确性容易验证
#include<bits/stdc++.h>
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 200100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
namespace CALC
{
inline int pls(int a,int b){return a+b>=MOD?a+b-MOD:(a+b<0?a+b+MOD:a+b);}
inline int mns(int a,int b){return a-b<0?a-b+MOD:(a-b>=MOD?a-b-MOD:a-b);}
inline int mul(int a,int b){return (1LL*a*b)%MOD;}
inline void inc(int &a,int b){a=pls(a,b);}
inline void dec(int &a,int b){a=mns(a,b);}
inline void tms(int &a,int b){a=mul(a,b);}
inline int qp(int x,int t,int res=1)
{for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(res,x);return res;}
inline int Inv(int x){return qp(x,MOD-2);}
}
using namespace CALC;
const ll inf=1e18;
int n,m;
int nxt[MAXN<<2],fst[MAXN<<1],to[MAXN<<2],val[MAXN<<2],cnt;
int vis[MAXN<<1],l[MAXN],r[MAXN];
struct Edge{int u,v,a,b;}e[MAXN];
bool operator < (Edge x,Edge y){return x.u<y.u||(x.u==y.u&&x.a<y.a);}
void add(int u,int v,int w){nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v,val[cnt]=w;}
struct node{int x;ll dis;};
bool operator < (node a,node b) {return a.dis>b.dis;}
ll dis[MAXN<<1];
priority_queue <node> q;
inline void dij()
{
int a;
rep(i,1,n+m) dis[i]=inf,vis[i]=0;dis[1]=0;
q.push((node){1,0});
while(!q.empty())
{
a=q.top().x;q.pop();if(vis[a]) continue;
vis[a]=1;
for(int i=fst[a];i;i=nxt[i])
if(dis[to[i]]>dis[a]+val[i])
{dis[to[i]]=dis[a]+val[i];if(!vis[to[i]]) q.push((node){to[i],dis[to[i]]});};
}
}
int main()
{
int v,ed;e[0].a=0,e[0].b=0;
rep(T,1,read())
{
n=read(),m=read();
rep(i,1,n) l[i]=r[i]=0;
rep(i,1,n+m) fst[i]=0;cnt=0;
rep(i,1,m) scanf("%d%d%d%d",&e[i].u,&e[i].v,&e[i].a,&e[i].b);
sort(e+1,e+m+1);
rep(i,1,m)
{
if(!l[e[i].u]) l[e[i].u]=i;
else add(i+n-1,i+n,0);
r[e[i].u]=i;
}
rep(i,1,n) if(r[i]) add(r[i]+n,i,0);
rep(i,1,m)
{
v=e[i].v;
if(!l[v]) ed=v;
else
{
ed=upper_bound(e+l[v],e+r[v]+1,(Edge){e[i].v,0,e[i].a,0})-e;
if(ed>r[v]) ed=v;else ed+=n;
}
add(e[i].u,ed,e[i].a);
add(i+n,ed,e[i].a-e[i].b);
}
dij();
rep(i,1,n) printf("%lld%c",dis[i]==inf?-1:dis[i],i==n?'\n':' ');
}
}
K
由于所有点权均不相同,因此对于当前的连通块
显然所有点都可以选择走到当前联通块内点权最大的点,然后把这个点删掉,继续递归这个过程
事实上由于删点难以做到,我们考虑按照权值从小到大加入每个点
每次遇到相邻的已经被访问过的连通块,就从这个新点向该连通块的根连边,这样每个点的深度即为答案
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 100100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
namespace CALC
{
inline int pls(int a,int b){return a+b>=MOD?a+b-MOD:(a+b<0?a+b+MOD:a+b);}
inline int mns(int a,int b){return a-b<0?a-b+MOD:(a-b>=MOD?a-b-MOD:a-b);}
inline int mul(int a,int b){return (1LL*a*b)%MOD;}
inline void inc(int &a,int b){a=pls(a,b);}
inline void dec(int &a,int b){a=mns(a,b);}
inline void tms(int &a,int b){a=mul(a,b);}
inline int qp(int x,int t,int res=1)
{for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(res,x);return res;}
inline int Inv(int x){return qp(x,MOD-2);}
}
using namespace CALC;
int n,nxt[MAXN<<1],to[MAXN<<1],cnt,fst[MAXN],dep[MAXN],vis[MAXN],fa[MAXN];
pii g[MAXN];
vector<int> G[MAXN];
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
void add(int u,int v){nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v;}
void dfs(int x,int pa)
{
dep[x]=dep[pa]+1;
for(auto v:G[x]) dfs(v,x);
}
int main()
{
int a,b,x;rep(T,1,read())
{
n=read();cnt=0;
rep(i,1,n) fa[i]=i,vis[i]=fst[i]=0,G[i].clear();
rep(i,2,n) a=read(),b=read(),add(a,b),add(b,a);
rep(i,1,n) g[i].fi=read(),g[i].se=i;
sort(g+1,g+n+1);
rep(i,1,n)
{
x=g[i].se;vis[x]=1;
ren if(vis[to[i]])
G[x].pb(find(to[i])),fa[find(to[i])]=x;
}
dfs(g[n].se,0);
rep(i,1,n) printf("%d\n",dep[i]);
}
}
比赛时候用了一种非常麻烦的做法
大概是按点权倒序加点,对每个点维护一个\(now_i\)
每次查询这个点到该点最近被访问过的祖先这条链上的\(now\)最大值\(+1\)即为答案
再把这条链上除最近被访问过的祖先以外的点的\(now\)用该点答案更新
查询祖先过程可以用二分+\(ST\)表预处理,修改与查询用树链剖分+线段树维护
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 200100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
namespace CALC
{
inline int pls(int a,int b){return a+b>=MOD?a+b-MOD:(a+b<0?a+b+MOD:a+b);}
inline int mns(int a,int b){return a-b<0?a-b+MOD:(a-b>=MOD?a-b-MOD:a-b);}
inline int mul(int a,int b){return (1LL*a*b)%MOD;}
inline void inc(int &a,int b){a=pls(a,b);}
inline void dec(int &a,int b){a=mns(a,b);}
inline void tms(int &a,int b){a=mul(a,b);}
inline int qp(int x,int t,int res=1)
{for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(res,x);return res;}
inline int Inv(int x){return qp(x,MOD-2);}
}
using namespace CALC;
int n,nxt[MAXN<<1],to[MAXN<<1],cnt,fst[MAXN],w[MAXN],h[MAXN],st[MAXN];
int fmx[MAXN][20],ff[MAXN][20];
pii g[MAXN];
int bl[MAXN],sz[MAXN],dep[MAXN],fa[MAXN],hvs[MAXN],in[MAXN],out[MAXN],dfn;
int mx[MAXN<<2],tag[MAXN<<2],ans[MAXN];
void add(int u,int v){nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v;}
void dfs(int x,int pa)
{
sz[x]=1,fa[x]=pa,fmx[x][0]=w[pa],ff[x][0]=fa[x],hvs[x]=0;
rep(j,1,19)
ff[x][j]=ff[ff[x][j-1]][j-1],fmx[x][j]=max(fmx[x][j-1],fmx[ff[x][j-1]][j-1]);
ren if(to[i]^pa)
{
dep[to[i]]=dep[x]+1;dfs(to[i],x);
sz[x]+=sz[to[i]],hvs[x]=sz[to[i]]>sz[hvs[x]]?to[i]:hvs[x];
}
}
void Dfs(int x,int anc)
{
bl[x]=anc,in[x]=out[x]=++dfn;
if(!hvs[x]) return ;Dfs(hvs[x],anc);
ren if(to[i]^fa[x]&&to[i]^hvs[x]) Dfs(to[i],to[i]);out[x]=dfn;
}
void build(int k,int l,int r)
{
tag[k]=mx[k]=0;if(l==r) return ;
int mid=l+r>>1;build(k<<1,l,mid);build(k<<1|1,mid+1,r);
}
inline void pshd(int k)
{
mx[k<<1]=mx[k<<1|1]=tag[k<<1]=tag[k<<1|1]=tag[k],tag[k]=0;
}
void mdf(int k,int l,int r,int a,int b,int x)
{
if(a<=l&&r<=b) {tag[k]=mx[k]=x;return;}int mid=l+r>>1;
if(tag[k]) pshd(k);
if(a<=mid) mdf(k<<1,l,mid,a,b,x);
if(b>mid) mdf(k<<1|1,mid+1,r,a,b,x);
mx[k]=max(mx[k<<1],mx[k<<1|1]);
}
int query(int k,int l,int r,int a,int b)
{
if(a<=l&&r<=b) return mx[k];int mid=l+r>>1,res=0;
if(tag[k]) pshd(k);
if(a<=mid) res=max(res,query(k<<1,l,mid,a,b));
if(b>mid) res=max(res,query(k<<1|1,mid+1,r,a,b));
return res;
}
inline int getmx(int x,int ww)
{
int res=0;dwn(i,19,0) if(ww&(1<<i))
res=max(res,fmx[x][i]),x=ff[x][i];
return res;
}
inline int getfa(int x,int ww)
{
dwn(i,19,0) if(ww&(1<<i))
x=ff[x][i];
return x;
}
int solve(int x,int y,int res=0)
{
for(;bl[x]!=bl[y];y=fa[bl[y]])
res=max(res,query(1,1,n,in[bl[y]],in[y]));
res=max(res,query(1,1,n,in[x],in[y]));
return res;
}
void work(int x,int y,int z)
{
for(;bl[x]!=bl[y];y=fa[bl[y]])
mdf(1,1,n,in[bl[y]],in[y],z);
if(in[x]<in[y]) mdf(1,1,n,in[x]+1,in[y],z);
}
int main()
{
int a,b;bl[0]=1;rep(T,1,read())
{
n=read();rep(i,1,n) fst[i]=0;dfn=cnt=0;
rep(i,2,n) a=read(),b=read(),add(a,b),add(b,a);
rep(i,1,n) w[i]=h[i]=read();sort(h+1,h+n+1);
rep(i,1,n) w[i]=lower_bound(h+1,h+n+1,w[i])-h,g[i]={w[i],i};
sort(g+1,g+n+1);
dfs(1,1);Dfs(1,1);
rep(i,1,n)
{
int l=1,r=dep[i],res=dep[i]+1,mid=l+r>>1;
for(;l<=r;mid=l+r>>1)
if(getmx(i,mid)>w[i]) res=mid,r=mid-1;
else l=mid+1;
if(res==dep[i]+1) st[i]=0;else st[i]=getfa(i,res);
}
build(1,1,n);
int x;dwn(i,n,1)
{
x=g[i].se;
ans[x]=solve(st[x],x)+1;
work(st[x],x,ans[x]);
}
rep(i,1,n) printf("%d\n",ans[i]);
}
}



