21牛客多校第九场

A

\[\sum\limits_{i=0}^{n}\sum\limits_{1\le cj\le ai+b}i^pj^q=\sum\limits_{i=0}^{n}\sum\limits_{j=1}^{\lfloor \frac{ai+b}{c}\rfloor}i^pj^q \]

令\(F(n)=\sum\limits_{i=0}^ni^q\)，有\(F(n)\)是关于\(n\)的\(q+1\)次多项式，设\(i\)次项系数为\(G[q][i]\)

\(G\)可以通过伯努利数求得，令\(S_t(n)=\sum_{i=0}^{n-1}i^t\)，有\(S_t(n)=\frac{1}{t+1}\sum\limits_{i=0}^t\binom{t+1}{i}B_in^{t+1-i}\)

由伯努利数的递推式\(B_t=-\frac{1}{t+1}\sum\limits_{i=0}^{t-1}\binom{t+1}{i}B_i\)求出伯努利数之后即得到\(G\)

\(G\)相较于\(S_t(n)\)仅多了\(n^t\)一项，该位系数\(+1\)即可

则原式为\(\sum\limits_{t=1}^{q+1}G_t\sum\limits_{i=0}^{n}i^p\lfloor \frac{ai+b}{c}\rfloor^t\)，后面为类欧几里得板子（这个\(G\)系数三角本身类欧板子也需要

类欧几里得是用来解决如下的问题：

\[F(n,a,b,c,k_1,k_2)=\sum\limits_{x=0}^{n}x^{k_1}\lfloor \frac{ax+b}{c}\rfloor^{k_2} \]

对于边界情况\(a=0||k_2=0\)显然可以通过预处理出的系数直接求解

对于\(a\ge c|| b\ge c\)的情况，可以将\(a\)拆为\(p+A,p=\lfloor\frac{a}{c}\rfloor,A=a\ mod\ c\)，同理将\(b\)拆为\(q+B\)，有：

\[\begin{aligned} F(n,a,b,c,k_1,k_2)&=\sum\limits_{x=0}^{n}x^{k_1}\lfloor \frac{ax+b}{c}\rfloor^{k_2}\\ &=\sum\limits_{x=0}^nx^{k_1}(px+q+\lfloor \frac{Ax+B}{c}\rfloor)^{k_2}\\ &=\sum\limits_{x=0}^nx^{k_1}\sum\limits_{i+j+k=k2}(px)^iq^j(\lfloor \frac{Ax+B}{c}\rfloor)^{k}\\ &=\sum\limits_{i+j+k=k2}p^iq^j\sum\limits_{x=0}^nx^{k_1+i}(\lfloor \frac{Ax+B}{c}\rfloor)^{k}\\ &=\sum\limits_{i=0}^{k_2}\sum\limits_{j=0}^{k_2-i}p^iq^j\sum\limits_{x=0}^nx^{k_1+i}(\lfloor \frac{Ax+B}{c}\rfloor)^{k_2-i-j}\\ &=\sum\limits_{i=0}^{k_2}\sum\limits_{j=0}^{k_2-i}p^iq^jF(n,A,B,c,k_1+i,k_2-i-j) \end{aligned} \]

枚举\(i,j\)后仍为递归形式

而当\(a,b<c\)时，有\(\lfloor \frac{a(x+1)+b}{c}\rfloor-\lfloor \frac{ax+b}{c}\rfloor\le 1\)因此\(\lfloor \frac{ax+b}{c}\rfloor\)存在上界\(m=\lfloor \frac{an+b}{c}\rfloor\)，有：

\[\begin{aligned} F(n,a,b,c,k_1,k_2)&=\sum\limits_{x=0}^{n}x^{k_1}\lfloor \frac{ax+b}{c}\rfloor^{k_2}\\ &=\sum\limits_{x=0}^{n}x^{k_1}(\sum\limits_{w=0}^{m-1}\left [ \lfloor \frac{ax+b}{c}\rfloor>w \right])^{k_2} \end{aligned} \]

差分一下有：

\[F(n,a,b,c,k_1,k_2)=\sum\limits_{x=0}^{n}x^{k_1}\sum\limits_{w=0}^{m-1}\left[\lfloor \frac{ax+b}{c}\rfloor>w\right]\left((w+1)^{k_2}-w^{k_2}\right) \]

将\(\lfloor \frac{ax+b}{c}\rfloor>w\)变形得：

\(\lfloor \frac{ax+b}{c}\rfloor\ge w+1\Leftrightarrow ax+b\ge c(w+1)\Leftrightarrow ax>cw+c-b-1\Leftrightarrow x>\lfloor\frac{cw+c-b-1}{a}\rfloor\)

原式即为：

\[\begin{aligned} F(n,a,b,c,k_1,k_2)&=\sum\limits_{x=0}^{n}x^{k_1}\sum\limits_{w=0}^{m-1}\left[x>\lfloor\frac{cw+c-b-1}{a}\rfloor\right]\left((w+1)^{k_2}-w^{k_2}\right)\\ &=\sum\limits_{w=0}^{m-1}\left((w+1)^{k_2}-w^{k_2}\right)\sum\limits_{x=0}^{n}x^{k_1}\left[x>\lfloor\frac{cw+c-b-1}{a}\rfloor\right]\\ &=\sum\limits_{w=0}^{m-1}\left((w+1)^{k_2}-w^{k_2}\right)\sum\limits_{x=0}^{n}x^{k_1}-\sum\limits_{w=0}^{m-1}\left((w+1)^{k_2}-w^{k_2}\right)\sum\limits_{x=0}^{\lfloor\frac{cw+c-b-1}{a}\rfloor}x^{k_1}\\ &=m^{k_2}\sum\limits_{x=0}^{n}x^{k_1}-\sum\limits_{w=0}^{m-1}\left((w+1)^{k_2}-w^{k_2}\right)\sum\limits_{x=0}^{\lfloor\frac{cw+c-b-1}{a}\rfloor}x^{k_1} \end{aligned} \]

其中\(k_1\)次幂和可以通过预处理\(G\)转化为多项式，前面容易处理，考虑后面一项，令\(\lfloor\frac{cw+c-b-1}{a}\rfloor=h\)：

\[\begin{aligned} &\sum\limits_{w=0}^{m-1}\left((w+1)^{k_2}-w^{k_2}\right)\sum\limits_{x=0}^{\lfloor\frac{cw+c-b-1}{a}\rfloor}x^{k_1}\\ =&\sum\limits_{w=0}^{m-1}\left((w+1)^{k_2}-w^{k_2}\right)\sum\limits_{j=0}^{k_1+1}G[k_1][j]\ h^j\\ =&\sum\limits_{w=0}^{m-1}\sum\limits_{i=0}^{k_2-1}\binom{k_2}{i}w^i\sum\limits_{j=0}^{k_1+1}G[k_1][j]\ h^j\\ =&\sum\limits_{i=0}^{k_2-1}\sum\limits_{j=0}^{k_1+1}\binom{k_2}{i}G[k_1][j]\sum\limits_{w=0}^{m-1}w^ih^j\\ =&\sum\limits_{i=0}^{k_2-1}\sum\limits_{j=0}^{k_1+1}\binom{k_2}{i}G[k_1][j]\sum\limits_{w=0}^{m-1}w^i\left(\lfloor\frac{cw+c-b-1}{a}\rfloor\right)^j\\ =&\sum\limits_{i=0}^{k_2-1}\sum\limits_{j=0}^{k_1+1}\binom{k_2}{i}G[k_1][j]\cdot F(m-1,c,c-b-1,a,i,j) \end{aligned} \]

同样为一个递归形式，由此即可写出整个类欧几里得模板

（由于\(a,c\)两项在不断的进行取模和交换，与辗转相除法十分类似，复杂度有所保证

同时过程中可以使用记忆化搜索优化

#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 1001001
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
namespace CALC
{
	inline int pls(int a,int b){return a+b>=MOD?a+b-MOD:(a+b<0?a+b+MOD:a+b);}
	inline int mns(int a,int b){return a-b<0?a-b+MOD:(a-b>=MOD?a-b-MOD:a-b);}
	inline int mul(int a,int b){return (1LL*a*b)%MOD;}
	inline void inc(int &a,int b){a=pls(a,b);}
	inline void dec(int &a,int b){a=mns(a,b);}
	inline void tms(int &a,int b){a=mul(a,b);}
	inline int qp(int x,int t,int res=1)
		{for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(res,x);return res;}
	inline int Inv(int x){return qp(x,MOD-2);}
}
using namespace CALC;
int n,C[210][210],B[210],G[210][210],fac[210],ifac[210],ans;
void mem(int n=205)
{
	rep(i,0,n) {C[i][0]=1;rep(j,1,i) C[i][j]=pls(C[i-1][j-1],C[i-1][j]);}
	fac[0]=ifac[0]=B[0]=1;int tmp;
	rep(i,1,n)
	{
		tmp=0;rep(j,0,i-1) tmp=pls(tmp,mul(C[i+1][j],B[j]));
		tmp=mns(0,tmp),B[i]=mul(tmp,Inv(i+1));
		fac[i]=mul(fac[i-1],i),ifac[i]=Inv(fac[i]);
	}
	rep(i,0,n)
	{
		tmp=Inv(i+1);
		rep(j,0,i) G[i][i+1-j]=mul(mul(tmp,C[i+1][j]),B[j]);
		inc(G[i][i],1);
	}
}
inline int calc(int n,int m)
{
	int res=0,pw=1;
	rep(i,0,m+1) inc(res,mul(G[m][i],pw)),tms(pw,n);
	return res;
}
int res[210][210][210];
int F(ll n,int a,int b,int c,int k1,int k2,int dep=0)
{
	if(~res[k1][k2][dep]) return res[k1][k2][dep];
	int &sum=res[k1][k2][dep]=0;
	if(!k2||!a) return sum=mul(calc(n,k1),qp(b/c,k2));
	if(a>=c||b>=c)
	{
		int p=a/c,q=b/c;
		for(int i=0,p1=1;i<=k2;i++,tms(p1,p))
			for(int j=0,p2=1;j<=k2-i;j++,tms(p2,q))
				inc(sum,mul(mul(mul(p1,p2),mul(mul(ifac[i],ifac[j]),mul(ifac[k2-i-j],fac[k2]))),
				F(n,a%c,b%c,c,k1+i,k2-i-j,dep+1)));
		return sum;
	}
	ll m=(n*a+b)/c;sum=mul(qp(m,k2),calc(n,k1));
	rep(i,0,k2-1) rep(j,0,k1+1)
		dec(sum,mul(mul(C[k2][i],G[k1][j]),F(m-1,c,c-b-1,a,i,j,dep+1)));
	return sum;
}
int main()
{
	mem();Fill(res,0xff);
	int a=read(),b=read(),c=read(),k1=read(),k2=read(),n=read();
	rep(i,1,k2+1) inc(ans,mul(G[k2][i],F(n,a,b,c,k1,i)));
	printf("%d\n",ans);
}

B

很玄的图论题咕

C

由\(LGV\)引理可知本题答案为

\[\begin{vmatrix} \binom{a_1+1}{1}&\binom{a_1+2}{2}&\cdots &\binom{a_1+n}{n}\\ \binom{a_2+1}{1}&\binom{a_2+2}{2}&\cdots &\binom{a_2+n}{n}\\ \vdots&\vdots&\ddots&\vdots\\ \binom{a_n+1}{1}&\binom{a_n+2}{2}&\cdots &\binom{a_n+n}{n} \end{vmatrix} =\prod\limits_{i=1}^n\frac{1}{i!}\begin{vmatrix} a_1+1&(a_1+1)(a_1+2)&\cdots &(a_1+1)\cdot \cdots \cdot(a_1+n)\\ a_2+1&(a_2+1)(a_2+2)&\cdots &(a_2+1)\cdot \cdots \cdot(a_2+n)\\ \vdots&\vdots&\ddots&\vdots\\ a_n+1&(a_n+1)(a_n+2)&\cdots &(a_n+1)\cdot \cdots \cdot(a_n+n)\\ \end{vmatrix} \]

可以都用第\(i\)列将\(i+1\)列中\(a_x+y\)的最大\(y\)这一项消掉，最终得到答案为

\[\prod\limits_{i=1}^n\frac{1}{i!}\begin{vmatrix} a_1+1&(a_1+1)^2&\cdots &(a_1+1)^n\\ a_2+1&(a_2+1)^2&\cdots &(a_2+1)^n\\ \vdots&\vdots&\ddots&\vdots\\ a_n+1&(a_n+1)^2&\cdots &(a_n+1)^n \end{vmatrix}=\prod\limits_{i=1}^n\frac{a_i+1}{i!}\begin{vmatrix} 1&(a_1+1)^1&\cdots &(a_1+1)^{n-1}\\ 1&(a_2+1)^1&\cdots &(a_2+1)^{n-1}\\ \vdots&\vdots&\ddots&\vdots\\ 1&(a_n+1)^1&\cdots &(a_n+1)^{n-1} \end{vmatrix} \]

该行列式为范德蒙德行列式，即\(ans=\prod\limits_{i=1}^n\frac{a_i+1}{i!}\prod\limits_{1\le j<i\le n}a_i-a_j\)

后半部分可以通过卷积求出所有差的出现次数得到答案

#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 2001001
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-b+MOD)%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,a[MAXN<<1],b[MAXN<<1],ifac[MAXN];
int rev[MAXN<<1],lim,lg,pw[30],ipw[30],ans=1;
int qp(int bas,int t,int res=1)
{
    for(;t;t>>=1,bas=mul(bas,bas)) if(t&1) res=mul(res,bas);return res;
}
#define inv(x) qp(x,MOD-2)
void ntt(int *a,int n,int f)
{
    rep(i,0,n-1) if(i<rev[i]) swap(a[i],a[rev[i]]);
    for(int i=1,t=1;i<n;i<<=1,++t)
    {
        int wn= f>0?pw[t]:ipw[t];for(int j=0;j<n;j+=i<<1)
        {
            int w=1,x,y;for(int k=0;k<i;++k,w=mul(w,wn))
                x=a[j+k],y=mul(a[j+k+i],w),a[j+k]=pls(x,y),a[j+k+i]=mns(x,y);
        }
    }
    if(f>0) return ;int nv=inv(n);rep(i,0,n-1) a[i]=mul(a[i],nv);
}
int main()
{
	n=read();a[0]++;rep(i,1,n) a[read()+1]++;ifac[0]=1;
	rep(i,1,n) ifac[i]=mul(ifac[i-1],inv(i)),ans=mul(ans,ifac[i]);
	n=1000005;rep(i,0,n) b[i]=a[n-i];
    for(lim=1,lg=1;lim<=(n+1<<1);lim<<=1,lg++)
        pw[lg]=qp(3,(MOD-1)/(1<<lg)),ipw[lg]=inv(pw[lg]);
    rep(i,1,lim-1) rev[i]=(rev[i>>1]>>1)|((i&1)<<lg-2);
    ntt(a,lim,1);ntt(b,lim,1);rep(i,0,lim-1) a[i]=mul(a[i],b[i]);ntt(a,lim,-1);
    rep(i,n+1,n<<1) if(a[i]) ans=mul(ans,qp(i-n,a[i]));
    printf("%d\n",ans);
}

D

奇怪构造题咕

E

由于从根开始的路径温度是递减的

因此只需要找到每个查询点向上最高满足限制的祖先，并在这个祖先的子树里查询\(t_i\ge l\)的点的个数即可

前者可以用倍增简单实现，后者可以对\(dfs\)序维护主席树实现

#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 100100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-(b))%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int lim=1e9;
int n,h[MAXN],g[MAXN],q,nxt[MAXN<<1],to[MAXN<<1],fst[MAXN],cnt;
int hsh[MAXN],dfn,in[MAXN],ou[MAXN],tt;
int rt[MAXN],w[MAXN<<7],ls[MAXN<<7],rs[MAXN<<7],tot,fa[MAXN][21];
void add(int u,int v) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v;}
void mdf(int &k,int kk,int l,int r,int x)
{
	w[k=++tot]=w[kk]+1,ls[k]=ls[kk],rs[k]=rs[kk];
	if(l==r) return ;int mid=l+r>>1;
	x<=mid?mdf(ls[k],ls[kk],l,mid,x):mdf(rs[k],rs[kk],mid+1,r,x);
}
int query(int k,int kk,int l,int r,int x)
{
	if(!k) return 0LL;if(l==r) return w[k]-w[kk];int mid=l+r>>1;
	if(x>mid) return query(rs[k],rs[kk],mid+1,r,x);
	else return w[rs[k]]-w[rs[kk]]+query(ls[k],ls[kk],l,mid,x);
}
void dfs(int x,int pa)
{
	fa[x][0]=pa,in[x]=++dfn,hsh[dfn]=x;ren if(to[i]^pa)
		dfs(to[i],x);ou[x]=dfn;
}
int main()
{
	n=read();int a,b,x,z;rep(i,2,n) a=read(),b=read(),add(a,b),add(b,a);
	rep(i,1,n) g[i]=read();
	dfs(1,1);
	rep(j,1,20) rep(i,1,n)
		fa[i][j]=fa[fa[i][j-1]][j-1];
	rep(i,1,n) mdf(rt[i],rt[i-1],1,lim,g[hsh[i]]);
	rep(Q,1,read())
	{
		z=x=read(),a=read(),b=read();
		if(g[x]>b||g[x]<a) {puts("0");continue;}
		dwn(j,20,0) if(g[fa[z][j]]<=b) z=fa[z][j];
		printf("%d\n",query(rt[ou[z]],rt[in[z]-1],1,lim,a));
	}
}

F

很猛的dp 咕

G

可做树\(dp\) 咕

H

对于位数相同的所有数，答案即为三进制分解

预处理位数\(\le i\)的数共有多少个即可

#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 100100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-(b))%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m,g[30];
ll pw[30],sum[30];
int main()
{
	n=read()-1;pw[0]=1;rep(i,1,29) pw[i]=pw[i-1]*3,sum[i]=sum[i-1]+pw[i];
	int pos=upper_bound(sum+1,sum+30,n)-sum-1;n-=sum[pos];
	rep(i,1,pos+1) g[++m]=n%3,n/=3;
	dwn(i,m,1)
		if(g[i]==0) cout<<2;
		else if(g[i]==1) cout<<3;
		else cout<<6;
}

I

奇妙式子题咕

J

右转显然和任何都不冲突，可以拿出来，而剩下的八种情况中每天至多同时存在两种，连边如下，答案为总和-最大匹配：

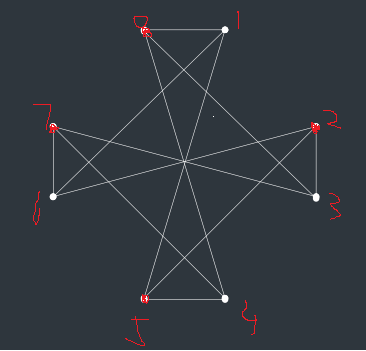
黑白染色之后发现同色点间仅\((1,6),(2,5)\)之间存在边，因此可以暴力枚举这两条边的匹配，然后剩下的跑二分图匹配

#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 15
#define MAXM 30
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
namespace CALC
{
	inline int pls(int a,int b){return a+b>=MOD?a+b-MOD:(a+b<0?a+b+MOD:a+b);}
	inline int mns(int a,int b){return a-b<0?a-b+MOD:(a-b>=MOD?a-b-MOD:a-b);}
	inline int mul(int a,int b){return (1LL*a*b)%MOD;}
	inline void inc(int &a,int b){a=pls(a,b);}
	inline void dec(int &a,int b){a=mns(a,b);}
	inline void tms(int &a,int b){a=mul(a,b);}
	inline int qp(int x,int t,int res=1)
		{for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(res,x);return res;}
	inline int Inv(int x){return qp(x,MOD-2);}
}
using namespace CALC;
struct Dinic
{
    int fst[MAXN],nxt[MAXM<<1],to[MAXM<<1],cnt,val[MAXM<<1];
    int vis[MAXN],q[MAXN],l,r,S,T,tot,dis[MAXN],cur[MAXN];
    void mem(){Fill(fst,0);cnt=1,tot=0;}
    void add(int u,int v,int w) {nxt[++cnt]=fst[u],fst[u]=cnt,to[cnt]=v,val[cnt]=w;}
    void ins(int u,int v,int w) {add(u,v,w);add(v,u,0);}
    int bfs()
    {
        vis[T]=++tot,dis[T]=0,q[l=r=1]=T;memcpy(cur,fst,sizeof(cur));
        int x;while(l<=r)
        {
            x=q[l++];ren if(val[i^1]&&vis[to[i]]!=tot)
                dis[to[i]]=dis[x]+1,vis[to[i]]=tot,q[++r]=to[i];
        }
        return vis[S]==tot;
    }
    int dfs(int x,int a)
    {
        if(x==T||!a) return a;int flw=0,f;
        for(int& i=cur[x];i&&a;i=nxt[i])
            if(val[i]&&dis[to[i]]==dis[x]-1&&(f=dfs(to[i],min(a,val[i]))))
                val[i]-=f,val[i^1]+=f,a-=f,flw+=f;
        return flw;
    }
    int solve(int ss,int tt,int res=0)
        {S=ss,T=tt;while(bfs()) res+=dfs(S,inf);return res;}
}D;
const int ln[]={0,2,5,7},rn[]={1,3,4,6};
int n,a[5][5],bas,ans,g[8],sum,res;
int main()
{
	int s=8,t=9;rep(T,1,read())
	{
		rep(i,0,3) rep(j,0,3) a[i][j]=read();
		bas=sum=ans=0;rep(i,0,3) bas=max(bas,a[i][(i+3)%4]);
		rep(i,0,3) g[i<<1]=a[i][(i+2)%4],g[i<<1|1]=a[i][(i+1)%4];
		rep(i,0,7) sum+=g[i];
		rep(x,0,min(g[1],g[6])) rep(y,0,min(g[2],g[5]))
		{
			D.mem();
			g[1]-=x,g[6]-=x,g[2]-=y,g[5]-=y;
			rep(i,0,3)
			{
				if(g[ln[i]]) D.ins(s,ln[i],g[ln[i]]);
				if(g[rn[i]]) D.ins(rn[i],t,g[rn[i]]);
			}
			D.ins(0,1,inf),D.ins(0,3,inf),D.ins(0,4,inf);
			D.ins(2,3,inf),D.ins(2,6,inf);
			D.ins(5,1,inf),D.ins(5,4,inf);
			D.ins(7,3,inf),D.ins(7,4,inf),D.ins(7,6,inf);
			res=D.solve(s,t),ans=max(ans,x+y+res);
			g[1]+=x,g[6]+=x,g[2]+=y,g[5]+=y;
		}
		ans=max(sum-ans,bas);
		printf("%d\n",ans);
	}
}

posted @ 2021-08-16 21:25 jack_yyc 阅读(59) 评论(0) 编辑收藏举报

刷新页面返回顶部

jack_yyc

蒟蒻

21牛客多校第九场

A

B

C

D

E

F

G

H

I

J

公告