21杭电多校第五场
A
LCT 咕
B
单位根反演 弃了
C
大胆猜测当\(n>k+1\)时无解
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 100100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-(b)+MOD)%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline ll read()
{
ll x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
ll n,k;
int main()
{
rep(T,1,read())
{
n=read(),k=read();
puts(n>k+1?"No":"Yes");
}
}
D
设\(dp[i][j]\)表示两字串分别从\(i,j\)开始满足\(k-\)匹配的最远处
通过先枚举\(j-i\)再\(dp\)可以通过双指针优化到\(O(1)\)转移,总复杂度\(O(n^2)\)
考虑\(dp[i][j]\)对答案的贡献,在\([\ i,dp[i][j]\ ]\)内贡献是一个递增的等差数列,在\([\ dp[i][j]+1,j-1\ ]\)内贡献是这个最大长度
分别对二阶差分和一阶差分打标记后求二阶前缀和即可
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 100100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-(b)+MOD)%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,k,dp[3030][3030];
ll ans[3030],res[3030];
char s[3030];
int main()
{
rep(T,1,read())
{
n=read(),k=read();scanf("%s",s+1);
int pos,sum;rep(i,1,n) ans[i]=res[i]=0;
rep(d,1,n)
{
sum=0,pos=n-d;
dwn(i,n-d,1)
{
sum+=(s[i]!=s[i+d]);
while((pos>=i+d||sum>k)&&pos>i) sum-=(s[pos]!=s[pos+d]),pos--;
dp[i][i+d]=sum>k?0:pos;
}
}
rep(i,1,n) rep(j,i+1,n) if(dp[i][j])
ans[i]++,ans[dp[i][j]+1]--,res[j]-=dp[i][j]-i+1;
rep(i,1,n-1) ans[i]+=ans[i-1];
rep(i,1,n-1) ans[i]+=ans[i-1]+res[i];
rep(i,1,n-1) printf("%d\n",ans[i]);
}
}
E
将对角线处的转移矩阵记为\(B\),将原转移矩阵的对角线赋值为\(0\)记为\(A\)
由定义出发,最终答案矩阵为\(I\sum\limits_{i=0}^{\infty}A^iB\),其中左侧的单位矩阵对应初始条件
则\(Ans=(\sum\limits_{i=0}^{\infty}A^i)B=\frac{A^{\infty}-I}{A-I}B=(A^{\infty}-I)(A-I)^{-1}B\)
由于\(A^{\infty}=\mathbf{0}\),则\(Ans=-(A-I)^{-1}B\),因此只需要对\((A-I)\)矩阵求逆
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 100100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-(b)+MOD)%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,a[350][350],p[350][700],sum[350],res[350][350];
void inc(int &x,int a) {x=pls(x,a);}
void dec(int &x,int a) {x=mns(x,a);}
void tms(int &x,int a) {x=mul(x,a);}
int inv(int bas,int res=1)
{
for(int t=MOD-2;t;t>>=1,bas=mul(bas,bas))
if(t&1) res=mul(res,bas);return res;
}
void mat_inv(int n)
{
int t,pos;rep(i,1,n)
{
pos=-1;rep(j,i,n) if(p[j][i]) {pos=j;break;}
if(pos==-1) return ;
swap(p[i],p[pos]);t=inv(p[i][i]);
rep(j,i,n<<1) tms(p[i][j],t);
rep(j,i+1,n) dwn(k,n<<1,i) dec(p[j][k],mul(p[i][k],p[j][i]));
}
dwn(i,n,1) rep(j,1,i-1) dwn(k,n<<1,i) dec(p[j][k],mul(p[i][k],p[j][i]));
}
int main()
{
rep(T,1,read())
{
n=read();rep(i,1,n) sum[i]=0;
rep(i,1,n) rep(j,1,n) p[i][j]=read(),p[i][j+n]=0,inc(sum[i],p[i][j]);
rep(i,1,n) sum[i]=inv(sum[i]);
rep(i,1,n) rep(j,1,n) tms(p[i][j],sum[i]);
rep(i,1,n) a[i][i]=p[i][i],p[i][i]=MOD-1,p[i][i+n]=1;
mat_inv(n);
rep(i,1,n) rep(j,1,n)
{
res[i][j]=0;
rep(k,1,n) dec(res[i][j],mul(p[i][k+n],a[k][j]));
}
rep(i,1,n) rep(j,1,n) printf("%d%c",res[i][j],j==n?'\n':' ');
}
}
F
签到题,直接按题意模拟建树操作
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 200100
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-(b)+MOD)%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,a[MAXN],ans;
void solve(int l,int r)
{
ans++;if(l==r) return ;if(r-l==1) {ans+=2;return ;}
int ml=l+(r-l+2)/3-1,mr=(ml+r)/2;
solve(l,ml);solve(ml+1,mr);solve(mr+1,r);
}
int main()
{
rep(T,1,read())
{
ans=0;n=read();rep(i,1,n) a[i]=read();
solve(1,n);printf("%d\n",ans);
}
}
G
对于最小值,铺满最下面一层和\(xOz\)、\(yOz\)平面,其中\(z\)轴不需要
对于最大值,从最高处掉\(n\)次
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 100100
#define MOD 1000000007
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-(b)+MOD)%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline ll read()
{
ll x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
ll n;int ans,s1,s2;
void inc(int &x,int a) {x=pls(x,a);}
int qp(int x,int t,int res=1)
{
for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(x,res);
return res;
}
#define inv(x) qp(x,MOD-2)
const int inv2=inv(2),inv6=inv(6);
int sum(int x){return mul(mul(x,x+1),inv2);}
int sum2(int x){return mul(mul(x,x+1),mul(2*x+1,inv6));}
int main()
{
rep(T,1,read())
{
n=read();n%=MOD,s1=sum(n),s2=sum2(n);
ans=mul(s1,s2);
inc(ans,mul(s1-1,s1-1));
inc(ans,mul(s1-1,s2-1));
printf("%lld\n",ans);ans=0;
ans=mul(s1,s2);ans=mul(ans,mul(n,n));
printf("%lld\n",ans);
}
}
H
根据条件概率公式,答案可以转化为
记\(sum[S]\)表示\(S\)的超集数量即\(sum[S]=\sum\limits_{S\subseteq A_i}1\),则\(Ans=\sum\limits_{S\in[0,2^n)}\sum\limits_{T\in[0,2^n)}\frac{sum[S \cup T]}{sum[S]}\)
而显然有\(S\subseteq\{S\cup T\}\),令\(sum2[S]=\sum\limits_{S\subseteq T}sum[T]\),对每个\(S\cup T\)显然有\(2^{bit[S]}\)个\(T\)使得\(S\cup T\)相同
因此\(Ans=\sum\limits_{S\in[0,2^n)}\frac{sum2[S]\cdot 2^{bit[S]}}{sum[S]}\),这两个求高位前缀和的过程可以使用\(fwt\)便利解决
#include<bits/stdc++.h>
#define inf 2139062143
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
#define MAXN 2001001
#define MOD 998244353
#define Fill(a,x) memset(a,x,sizeof(a))
#define rep(i,s,t) for(int i=(s),i##end=(t);i<=i##end;++i)
#define dwn(i,s,t) for(int i=(s),i##end=(t);i>=i##end;--i)
#define ren for(int i=fst[x];i;i=nxt[i])
#define pls(a,b) (a+b)%MOD
#define mns(a,b) (a-(b)+MOD)%MOD
#define mul(a,b) (1LL*(a)*(b))%MOD
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int s[MAXN],s2[MAXN],bit[MAXN],ans,n,m,mxs;
int qp(int x,int t,int res=1)
{
for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(x,res);
return res;
}
void fwt(int *a,int n)
{
for(int i=1;i<n;i<<=1) for(int j=0;j<n;j+=i<<1) rep(k,0,i-1)
a[j+k]+=a[j+k+i];
}
int main()
{
rep(T,1,read())
{
n=read(),m=read(),mxs=(1<<n)-1,ans=0;int res;
rep(i,0,mxs) s[i]=s2[i]=0,bit[i]=i?bit[i-(i&-i)]+1:0;
rep(i,1,m) s[read()]++;fwt(s,1<<n);
rep(i,0,mxs) s2[i]=s[i];fwt(s2,1<<n);
rep(i,0,mxs)
{
res=qp(s[i],MOD-2,s2[i]);
ans=pls(ans,mul(res,1<<bit[i]));
}
printf("%d\n",ans);
}
}
I
和一道原来的题一样,但线段树维护一次函数直接\(T\)飞了
先枚举那个众数\(x\),令\(sum_i=sum_{i-1}+(a_i==x?1:-1)\)
则对于每个\((i,sum_i)\),答案即为满足\(j<i,sum_j<sum_i\)的\(j\)的个数
直接加入每个点显然复杂度过高,而上升点的总数为\(n\)
考虑如何快速维护一段下降的贡献,对于\(sum\)值进行差分,则所求即为这个差分数组的二阶前缀和
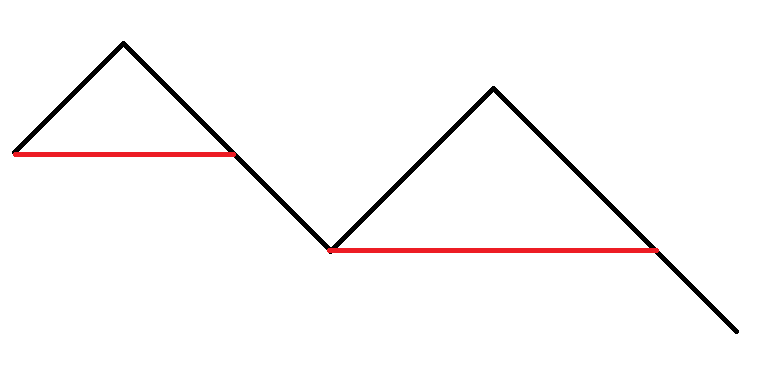
对于这样一个图像,我们对于红线上方的点暴力维护差分数组以及差分数组的一二阶前缀和用来统计答案,而红线到下一次最小值之间的点并不会作为右端点对答案有贡献,因此我们可以暴力计算所有红线上方点的贡献
#include<bits/stdc++.h>
#define rep(i,s,t) for(int i=(s),i__end=(t);i<=i__end;++i)
#define dwn(i,s,t) for(int i=(s),i__end=(t);i>=i__end;++i)
#define ren(x) for(register int i=fst[x];i;i=nxt[i])
#define pb(a,x) vec[a].push_back(x);
#define ll long long
#define inf 2139062143
#define MAXN 1001001
using namespace std;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,g[MAXN],hsh[MAXN],m,del[MAXN<<2],tp,tag[MAXN<<1];
ll sum,ans,now,tot;int mn;
vector<int> vec[MAXN];
void work(int id)
{
pb(id,n+1);//cout<<id<<"\n";
del[1]=0,del[tp=2]=1;tag[0+n]++,tag[1+n]--;
mn=sum=now=0,tot=1;int las=0,lim;
for(auto x:vec[id])
{
//cout<<x<<" "<<now<<" "<<tot<<" "<<sum<<" "<<ans<<endl;
if(x!=las+1)
{
int tmp=now;
for(lim=now-(x-las)+1;now>max(lim,mn);now--)
tot-=tag[now+n],sum-=tot,ans+=sum;
//cout<<lim<<" "<<mn<<" "<<now<<endl;
if(mn>lim) mn=now=lim,tot=0,sum=0;
tot++;del[++tp]=now,tag[now+n]++;
del[++tp]=tmp,tag[tmp+n]--;
}
if(x==n+1) break;
sum+=tot,ans+=sum;
now++,del[++tp]=now,tag[now+n]++,del[++tp]=now+1,tag[now+1+n]--;
tot+=tag[now+n],las=x;
//cout<<x<<" "<<now<<" "<<tot<<" "<<sum<<" "<<ans<<endl;
}
while(tp) tag[del[tp]+n]=0,tp--;
}
int main()
{
rep(T,1,read())
{
n=read();rep(i,1,n) {g[i]=read();if(!hsh[g[i]]) hsh[g[i]]=++m;}
rep(i,1,n) pb(hsh[g[i]],i);
rep(i,1,m) work(i);printf("%lld\n",ans);
rep(i,1,n) hsh[g[i]]=0;rep(i,1,m) vec[i].clear();m=0;ans=0;
}
}
J
概率论 不会
K
奇怪的博弈 咕
L
生成函数,多项式快速幂 咕



