【系列】 莫比乌斯反演
几个有用的结论:
记狄利克雷卷积: $(f*g)(n)=\sum\limits_{d|n} f(d) * g(\frac{n}{d})$
则有重要结论:$\mu * 1 = [n=1]$与$\varphi *1 = id$与$\mu * id=\varphi$
若$F(n)=\sum\limits_{d|n} f(d)$
则$f(n)=\sum\limits_{d|n} \mu(d) * F(\frac{n}{d})$
bzoj 2190 仪仗队
题目大意:
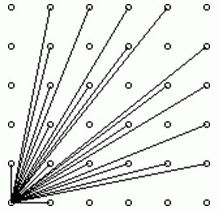
求$n*n$的矩形中能从左下角被直接看到的点的个数
思路:
设左下角$(0,0)$ 则相当于求$\sum\limits_{i=1}^{n-1} \sum\limits_{j=1}^{n-1} [gcd(i,j)==1]+2$($(1,0),(0,1)$
将式子转化为$1+ 2* \sum\limits_{i=1}^{n-1} \sum\limits_{j=1}^{i} [gcd(i,j)==1] $(由于有$(1,0),(0,1),(1,1)$三个特殊点存在
然后发现满足欧拉函数的定义,则所求为$1+2* \sum\limits_{i=1}^{n-1} \varphi(i) $ 筛出欧拉函数即可

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 #include<map> 10 #include<set> 11 #define ll long long 12 #define db double 13 #define inf 2139062143 14 #define MAXN 50010 15 #define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i) 16 #define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i) 17 #define ren for(register int i=fst[x];i;i=nxt[i]) 18 #define pb(i,x) vec[i].push_back(x) 19 #define pls(a,b) (a+b)%MOD 20 #define mns(a,b) (a-b+MOD)%MOD 21 #define mul(a,b) (1LL*(a)*(b))%MOD 22 using namespace std; 23 inline int read() 24 { 25 int x=0,f=1;char ch=getchar(); 26 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 27 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 28 return x*f; 29 } 30 int n,tot,p[MAXN+100],ntp[MAXN+100],phi[MAXN+100]; 31 void mem() 32 { 33 phi[1]=1; 34 rep(i,2,MAXN) 35 { 36 if(!ntp[i]) p[++tot]=i,phi[i]=i-1; 37 rep(j,1,tot) if(i*p[j]>MAXN) break; 38 else {ntp[i*p[j]]=1;if(i%p[j]) phi[i*p[j]]=phi[i]*phi[p[j]];else {phi[i*p[j]]=phi[i]*p[j];break;}} 39 } 40 rep(i,2,n-1) phi[i]+=phi[i-1]; 41 } 42 int main() 43 { 44 n=read();mem();printf("%d\n",n>1?phi[n-1]<<1|1:0); 45 }
bzoj 2818 Gcd
题目大意:
求有序数对$(i,j),i,j \leq n$满足$gcd(i,j)$为素数的数对个数
思路:
法1:和上一题很相似,设$p$为素数则$\sum\limits_{i=1}^n \sum\limits_{j=1}^n [gcd(i,j)==p] =\sum\limits_{i=1}^{n/p} \sum\limits_{j=1}^{n/p} [gcd(i,j)==1]$
这样我们枚举每一个素数就可以解决了

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 #include<map> 10 #include<set> 11 #define ll long long 12 #define db double 13 #define inf 2139062143 14 #define MAXN 10001000 15 #define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i) 16 #define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i) 17 #define ren for(register int i=fst[x];i;i=nxt[i]) 18 #define pb(i,x) vec[i].push_back(x) 19 #define pls(a,b) (a+b)%MOD 20 #define mns(a,b) (a-b+MOD)%MOD 21 #define mul(a,b) (1LL*(a)*(b))%MOD 22 using namespace std; 23 inline int read() 24 { 25 int x=0,f=1;char ch=getchar(); 26 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 27 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 28 return x*f; 29 } 30 int n,tot,p[MAXN],ntp[MAXN+5],phi[MAXN]; 31 ll ans,sum[MAXN]; 32 void mem() 33 { 34 phi[1]=1; 35 rep(i,2,n) 36 { 37 if(!ntp[i]) p[++tot]=i,phi[i]=i-1; 38 rep(j,1,tot) if(i*p[j]>n) break; 39 else {ntp[i*p[j]]=1;if(i%p[j]) phi[i*p[j]]=phi[i]*phi[p[j]];else {phi[i*p[j]]=phi[i]*p[j];break;}} 40 } 41 rep(i,1,n) sum[i]=sum[i-1]+phi[i]; 42 } 43 int main() 44 { 45 n=read();mem(); 46 rep(i,1,tot) ans+=sum[n/p[i]]*2-1;printf("%lld\n",ans); 47 }
法2:因为$gcd(i,j)==1$的形式可以转化为$\sum\limits_{d|gcd(i,j)} \mu(d)$
由于对于每一个$d$,相对应的$i,j$有$n/i,n/j$个。所以前两个枚举是没有必要的,设$m$为$n/p$,式子为$\sum\limits_{d=1}^m \mu(d)*\frac{m}{d}*\frac{m}{d}$
枚举素数后数论分块

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 #include<map> 10 #include<set> 11 #define ll long long 12 #define db double 13 #define inf 2139062143 14 #define MAXN 10001000 15 #define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i) 16 #define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i) 17 #define ren for(register int i=fst[x];i;i=nxt[i]) 18 #define pb(i,x) vec[i].push_back(x) 19 #define pls(a,b) (a+b)%MOD 20 #define mns(a,b) (a-b+MOD)%MOD 21 #define mul(a,b) (1LL*(a)*(b))%MOD 22 using namespace std; 23 inline int read() 24 { 25 int x=0,f=1;char ch=getchar(); 26 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 27 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 28 return x*f; 29 } 30 int n,tot,p[MAXN],ntp[MAXN+5],mu[MAXN]; 31 ll ans,sum[MAXN]; 32 void mem() 33 { 34 mu[1]=1; 35 rep(i,2,n) 36 { 37 if(!ntp[i]) p[++tot]=i,mu[i]=-1; 38 rep(j,1,tot) if(i*p[j]>n) break; 39 else {ntp[i*p[j]]=1;if(i%p[j]) mu[i*p[j]]=-mu[i];else {mu[i*p[j]]=0;break;}} 40 } 41 rep(i,1,n) sum[i]=sum[i-1]+mu[i]; 42 } 43 ll solve(int x,ll res=0) 44 { 45 int pos,lmt=n/x;rep(i,1,lmt) {pos=lmt/(lmt/i);res+=1LL*(sum[pos]-sum[i-1])*(lmt/i)*(lmt/i);i=pos;} 46 return res; 47 } 48 int main() 49 { 50 n=read();mem(); 51 rep(i,1,tot) ans+=solve(p[i]);printf("%lld\n",ans); 52 }
bzoj 1101 Zap
题目大意:
求有序数对$(i,j),i\leq a,j \leq b$满足$gcd(i,j)==d$的数对个数
思路:
和上一题基本一样

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 #include<map> 10 #include<set> 11 #define ll long long 12 #define db double 13 #define inf 2139062143 14 #define MAXN 60100 15 #define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i) 16 #define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i) 17 #define ren for(register int i=fst[x];i;i=nxt[i]) 18 #define pb(i,x) vec[i].push_back(x) 19 #define pls(a,b) (a+b)%MOD 20 #define mns(a,b) (a-b+MOD)%MOD 21 #define mul(a,b) (1LL*(a)*(b))%MOD 22 using namespace std; 23 inline int read() 24 { 25 int x=0,f=1;char ch=getchar(); 26 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 27 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 28 return x*f; 29 } 30 int n,tot,p[MAXN],ntp[MAXN+5],mu[MAXN]; 31 ll ans,sum[MAXN]; 32 void mem(int n) 33 { 34 mu[1]=1; 35 rep(i,2,n) 36 { 37 if(!ntp[i]) p[++tot]=i,mu[i]=-1; 38 rep(j,1,tot) if(i*p[j]>n) break; 39 else {ntp[i*p[j]]=1;if(i%p[j]) mu[i*p[j]]=-mu[i];else {mu[i*p[j]]=0;break;}} 40 } 41 rep(i,1,n) sum[i]=sum[i-1]+mu[i]; 42 } 43 ll solve(int x,int y,ll res=0) 44 { 45 int pos,lmt=min(x,y);rep(i,1,lmt) 46 {pos=min(x/(x/i),(y/(y/i)));res+=1LL*(sum[pos]-sum[i-1])*(x/i)*(y/i);i=pos;} 47 return res; 48 } 49 int main() 50 { 51 int T=read(),a,b,d;mem(50010);while(T--) 52 {a=read(),b=read(),d=read();printf("%lld\n",solve(a/d,b/d));} 53 }
bzoj 4804 欧拉心算
题目大意:
求$\sum\limits_i^n \sum\limits_j^n \varphi(gcd(i,j))$
思路:
枚举$gcd$ 得到$\sum\limits_{k=1}^n \varphi(k) \sum\limits_{i=1}^n \sum\limits_{j=1}^n [gcd(i,j)==k]$
后面的式子转化为第一题的样子即原式为$\sum\limits_{k=1}^n \varphi(k) (-1+2*\sum\limits_{i=1}^{n/k}\varphi(i))$
设$f(k)=-1+2*\sum\limits_{i=1}^k \varphi(i)$ 则原式为$\sum\limits_{k=1}^n \varphi(k)*f(\frac{n}{k})$
使用数论分块即可

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 #include<map> 10 #include<set> 11 #define ll long long 12 #define db double 13 #define inf 2139062143 14 #define MAXN 10000001 15 #define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i) 16 #define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i) 17 #define ren for(register int i=fst[x];i;i=nxt[i]) 18 #define pb(i,x) vec[i].push_back(x) 19 #define pls(a,b) (a+b)%MOD 20 #define mns(a,b) (a-b+MOD)%MOD 21 #define mul(a,b) (1LL*(a)*(b))%MOD 22 using namespace std; 23 inline int read() 24 { 25 int x=0,f=1;char ch=getchar(); 26 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 27 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 28 return x*f; 29 } 30 int n,tot,p[MAXN],ntp[MAXN]; 31 ll ans,phi[MAXN],f[MAXN]; 32 void mem(int n) 33 { 34 phi[1]=1; 35 rep(i,2,n) 36 { 37 if(!ntp[i]) p[++tot]=i,phi[i]=i-1; 38 rep(j,1,tot) if(i*p[j]>n) break; 39 else {ntp[i*p[j]]=1;if(i%p[j]) phi[i*p[j]]=phi[i]*phi[p[j]];else {phi[i*p[j]]=phi[i]*p[j];break;}} 40 } 41 rep(i,1,n) phi[i]+=phi[i-1],f[i]=-1+(phi[i]<<1); 42 } 43 ll solve(int n,ll res=0) 44 { 45 int pos;rep(i,1,n) {pos=n/(n/i);res+=1LL*(phi[pos]-phi[i-1])*f[n/i];i=pos;}return res; 46 } 47 int main() 48 { 49 int T=read(),a,b,d;mem(10000000);while(T--) 50 {a=read();printf("%lld\n",solve(a));} 51 }
(卡我一个数组的空间常数怕不是有毒
bzoj 3529 数表
题目大意:
有一张 n×m 的数表,其第 i 行第 j 列(1 <= i <= n, 1 <= j <= m)的数值为能同时整除 i 和 j 的所有自然数之和
q次询问 每次给出n m a 求数表中不大于 a 的数之和
思路:
首先设$f(i)=\sum\limits_{d|i} d$
则所求为$\sum\limits_{i=1}^n \sum\limits_{j=1}^m f(gcd(i,j)) *[f(gcd(i,j))<=a]$
先不管最后那一个限制,继续推式子,我们枚举$gcd$:$\sum\limits_{k=1}^n f(k) \sum\limits_{i=1}^{n/k} \sum\limits_{j=1}^{m/k} [gcd(i,j)==1]$
后面的式子好熟啊,变成莫比乌斯函数形式:$\sum\limits_{k=1}^n f(k) \sum\limits_d^{min(n/k,m/k)} \mu(d) \frac{n/k}{d} \frac{m/k}{d}$
如果后面把$k$写在分数线下面,发现我们可以枚举$k*d$设为$t$ 得到:$\sum\limits_{t=1}^{min(n,m)} \frac{n}{t} \frac{m}{t} \sum\limits_{i|t} f(i)*\mu(\frac{t}{i})$
把后面的拿出来设$h(t)=\sum\limits_{i|t} f(i)*\mu(\frac{t}{i})$ 原式为$\sum\limits_{t=1}^{min(n,m)} h(t) \frac{n}{t} \frac{m}{t}$我们可以数论分块
对于$h(i)$,我们可以把询问的$a$限制从小到大排序,将所有$i$按照$f(i)$排序后一次加入
每一个$i$,枚举其倍数$t=k *i $即对$h(t)$造成的影响,其复杂度为调和级数,暴力使用树状数组维护对每个倍数的位置$pos(i*j)+=f(i)*\mu(j)$
数论分块的时候前缀和用树状数组查询即可

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 #include<map> 10 #include<set> 11 #define ll long long 12 #define db double 13 #define inf 2139062143 14 #define MAXN 100100 15 #define MOD 2147483647 16 #define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i) 17 #define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i) 18 #define ren for(register int i=fst[x];i;i=nxt[i]) 19 #define pb(i,x) vec[i].push_back(x) 20 #define pls(a,b) (a+b)%MOD 21 #define mns(a,b) (a-b+MOD)%MOD 22 #define mul(a,b) (1LL*(a)*(b))%MOD 23 using namespace std; 24 inline int read() 25 { 26 int x=0,f=1;char ch=getchar(); 27 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 28 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 29 return x*f; 30 } 31 int n,tot,p[MAXN],ntp[MAXN],mu[MAXN],lmt; 32 ll phi[MAXN],f[MAXN],g[MAXN],ans[MAXN],af[MAXN]; 33 struct Ask{int id,n,m,a;}q[MAXN]; 34 bool cmpa(Ask x,Ask y) {return x.a<y.a;} 35 bool cmp(int a,int b) {return f[a]<f[b];} 36 ll c[MAXN]; 37 int lowbit(int x) {return x&(-x);} 38 void mdf(int x,int val) {for(;x<=lmt;x+=lowbit(x)) (c[x]+=val)&=MOD;} 39 ll query(int x,ll res=0) {for(;x;x-=lowbit(x)) (res+=c[x])&=MOD;return res;} 40 void mem(int n) 41 { 42 mu[1]=1;rep(i,2,n) 43 { 44 if(!ntp[i]) p[++tot]=i,mu[i]=-1; 45 rep(j,1,tot) if(i*p[j]>n) break; 46 else {ntp[i*p[j]]=1;if(i%p[j]) mu[i*p[j]]=-mu[i];else {mu[i*p[j]]=0;break;}} 47 } 48 rep(i,1,n) for(int j=af[i]=i;j<=n;j+=i) f[j]=(f[j]+i)&MOD; 49 } 50 ll solve(int n,int m,ll res=0) 51 { 52 int pos;rep(i,1,min(n,m)) 53 {pos=min(n/(n/i),m/(m/i));(res+=1LL*(query(pos)-query(i-1))*(((n/i)*(m/i))&MOD))&=MOD;i=pos;} 54 return res; 55 } 56 int main() 57 { 58 int num=read(),a,b,d;mem(lmt=100000); 59 rep(i,1,num) q[i].n=read(),q[i].m=read(),q[i].a=read(),q[i].id=i; 60 sort(q+1,q+num+1,cmpa);sort(af+1,af+lmt+1,cmp);int pos=1; 61 rep(i,1,num) 62 { 63 while(pos<lmt&&f[af[pos]]<=q[i].a) 64 {rep(j,1,lmt/af[pos]) mdf(af[pos]*j,f[af[pos]]*mu[j]);pos++;} 65 ans[q[i].id]=solve(q[i].n,q[i].m); 66 } 67 rep(i,1,num) printf("%d\n",ans[i]); 68 }
bzoj 2154 Crash的数字表格
题目大意:
求$\sum\limits_{i=1}^n \sum\limits_{j=1}^m lcm(i,j)$
思路:
先将$lcm$转化为$gcd$:$\sum\limits_{i=1}^n \sum\limits_{j=1}^m \frac{i*j}{gcd(i,j)}$
令$n$为较小的那个数,然后枚举一波gcd:$\sum\limits_{d=1}^n \sum\limits_{i=1}^{n/d} \sum\limits_{j=1}^{m/d} \frac{id*jd}{d} *[gcd(i,j)==1]$
把$d$提到前面去接化简后面那个很熟的式子:$\sum\limits_{d=1}^n d* \sum\limits_{i=1}^{n/d} \sum\limits_{j=1}^{m/d} \sum\limits_{t|gcd(i,j)} i*j*\mu(t)$
对于第二个$gcd$继续枚举:$\sum\limits_{d=1}^n d * \sum\limits_{t=1}^{n/d} \sum\limits_{i=1}^{n/(dt)} \sum\limits_{j=1}^{m/(dt)} it *jt*\mu(t)$
提出$t$: $\sum\limits_{d=1}^n d *( \sum\limits_{t=1}^{n/d} t^2 * \mu(t)) \sum\limits_{i=1}^{n/(dt)} i *\sum\limits_{j=1}^{m/(dt)} j$
设$s(t)=\sum\limits_{i=1}^t i$,则:$\sum\limits_{d=1}^n d * \sum\limits_{t=1}^{n/d} t^2 * \mu(t) * s(\frac{n}{dt}) *s(\frac{m}{dt})$
与前一题类似的,我们设$g=d*t$,得到:$\sum\limits_{g=1}^n \sum\limits_{d|g} d * \mu(\frac{g}{d}) * (\frac{g}{d})^2 * s(\frac{n}{g}) * s(\frac{m}{g})$
把$g$提出来:$\sum\limits_{g=1}^n g * s(\frac{n}{g}) * s(\frac{m}{g})\sum\limits_{d|g} \frac{g}{d}* \mu(\frac{g}{d}) $
把后面的部分单独拿出来,设$f(g)=\sum\limits_{d|g} d * \mu(d)$,发现$f$是$d*\mu(d)$与$1$的狄利克雷卷积结果
由于那两个都是积性函数,因此$f$也是积性函数,可以通过筛法来求
对于素数$p$,两个因数分别$1,p$,因此$f(p)=-p+1$
对于线筛中$i%p[j]==0$的情况,考虑新增添的因数一定含有平方因子,因此其莫比乌斯函数一定为0,不需要考虑
最终式子为$\sum\limits_{g=1}^n g * s(\frac{n}{g}) * s(\frac{m}{g}) *f(g) $然后愉快的数论分块即可

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<algorithm> 7 #include<queue> 8 #include<vector> 9 #include<map> 10 #include<set> 11 #define ll long long 12 #define db double 13 #define inf 2139062143 14 #define MAXN 10001000 15 #define MOD 20101009 16 #define rep(i,s,t) for(register int i=(s),i##__end=(t);i<=i##__end;++i) 17 #define dwn(i,s,t) for(register int i=(s),i##__end=(t);i>=i##__end;--i) 18 #define ren for(register int i=fst[x];i;i=nxt[i]) 19 #define pb(i,x) vec[i].push_back(x) 20 #define pls(a,b) (a+b+MOD)%MOD 21 #define mns(a,b) (a-b+MOD)%MOD 22 #define mul(a,b) (1LL*(a)*(b))%MOD 23 using namespace std; 24 inline int read() 25 { 26 int x=0,f=1;char ch=getchar(); 27 while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();} 28 while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();} 29 return x*f; 30 } 31 int n,m,tot,p[MAXN],ntp[MAXN],lmt; 32 ll f[MAXN],s[MAXN]; 33 void mem(int n) 34 { 35 f[1]=1;rep(i,2,n) 36 { 37 if(!ntp[i]) p[++tot]=i,f[i]=-i+1; 38 rep(j,1,tot) if(i*p[j]>n) break; 39 else {ntp[i*p[j]]=1;if(i%p[j]) f[i*p[j]]=mul(f[i],f[p[j]]);else {f[i*p[j]]=f[i];break;}} 40 } 41 rep(i,1,n) s[i]=pls(s[i-1],i),f[i]=pls(f[i-1],mul(f[i],i)); 42 } 43 ll solve(int n,int m,ll res=0) 44 { 45 int pos;rep(i,1,min(n,m)) 46 {pos=min(n/(n/i),m/(m/i));res=pls(res,mul(f[pos]-f[i-1],mul(s[n/i],s[m/i])));i=pos;} 47 return res; 48 } 49 int main() 50 { 51 n=read(),m=read();mem(max(n,m));printf("%lld\n",solve(n,m)); 52 }
bzoj 4816 数字表格
题目大意:
求$\prod\limits_{i=1}^n \prod\limits_{j=1}^m F(gcd(i,j))$ 其中$F(i)$表示斐波那契数列的第$i$项
思路:
首先经典枚举$gcd$,不妨设$n<m$变形后得到:$\prod\limits_{d=1}^n \prod\limits_{i=1}^{n/d} \prod\limits_{j=1}^{m/d} F(d)*[(i,j)==1]$
反演后得到$\prod\limits_{d=1}^n F(d)^{\sum\limits_{t=1}^{n/d} \mu(t)*\frac{n}{dt}*\frac{m}{dt}}$
经典换元$g=dt$后得到:$\prod\limits_{g=1}^n (\prod\limits_{d|g} F(\frac{g}{d})^{\mu(d)})^{\frac{n}{dt}*\frac{m}{dt}}$
此时只需考虑里面的$\prod\limits_{d|g} F(\frac{g}{d})^{\mu(d)}$如何快速求出
由于$n\le 10^6$,可以通过枚举$d$用一个$nlog$n的时间预处理出里面的前缀积
最后只需要数论分块即可

1 #include<bits/stdc++.h> 2 #define inf 2139062143 3 #define MAXN 1001001 4 #define MOD 1000000007 5 #define ll long long 6 #define ull unsigned long long 7 #define rep(i,s,t) for(register int i=(s),i##end=(t);i<=i##end;++i) 8 #define dwn(i,s,t) for(register int i=(s),i##end=(t);i>=i##end;--i) 9 #define ren for(register int i=fst[x];i;i=nxt[i]) 10 #define Fill(a,b) memset(a,b,sizeof(a)) 11 #define pls(a,b) ((a+b)%MOD+MOD)%MOD 12 #define mns(a,b) (((a)-(b))%MOD+MOD)%MOD 13 #define mul(a,b) (1LL*(a)*(b)%MOD) 14 #define pii pair<int,int> 15 #define mp(a,b) make_pair(a,b) 16 #define pb(i,x) vec[i].push_back(x) 17 #define fi first 18 #define se second 19 using namespace std; 20 inline int read() 21 { 22 int x=0;bool f=1;char ch=getchar(); 23 while(!isdigit(ch)) {if(ch=='-') f=0;ch=getchar();} 24 while(isdigit(ch)) x=x*10+(ch^48),ch=getchar(); 25 return f?x:-x; 26 } 27 int ntp[MAXN],p[MAXN],mu[MAXN],tot,g[MAXN],pre[MAXN],f[MAXN],fi[MAXN]; 28 int qp(int x,int t,int res=1) 29 { 30 for(;t;t>>=1,x=mul(x,x)) if(t&1) res=mul(res,x);return res; 31 } 32 #define inv(x) qp(x,MOD-2) 33 void mem(int n) 34 { 35 f[1]=fi[1]=1;rep(i,2,n) f[i]=pls(f[i-1],f[i-2]),fi[i]=inv(f[i]); 36 mu[1]=1;rep(i,2,n) 37 { 38 if(!ntp[i]) p[++tot]=i,mu[i]=-1; 39 rep(j,1,tot) if(1LL*i*p[j]>n) break; 40 else {ntp[i*p[j]]=1;if(i%p[j]) mu[i*p[j]]=-mu[i];else break;} 41 } 42 rep(i,0,n) g[i]=pre[i]=1; 43 rep(i,1,n) rep(j,1,n/i) 44 if(mu[j]) g[i*j]=mul(g[i*j],mu[j]==1?f[i]:fi[i]); 45 rep(i,1,n) pre[i]=mul(g[i],pre[i-1]); 46 } 47 int solve(int x,int y,int res=1) 48 { 49 int r;rep(l,1,min(x,y)) 50 r=min(x/(x/l),y/(y/l)),res=mul(res,qp(mul(pre[r],inv(pre[l-1])),(1LL*(x/l)*(y/l))%(MOD-1))),l=r; 51 return res; 52 } 53 int main() 54 { 55 int T=read(),n,m;mem(1000000); 56 while(T--) {n=read(),m=read();printf("%d\n",solve(n,m));} 57 }




