BZOJ 1912 patrol 巡逻

Description

Input

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1行，每行两个整数 a, b， 表示村庄a与b之间有一条道路(1 ≤ a, b ≤ n)。

Output

输出一个整数，表示新建了K 条道路后能达到的最小巡逻距离。

Sample Input

8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6

Sample Output

11

HINT

10%的数据中，n ≤ 1000, K = 1；
30%的数据中，K = 1；
80%的数据中，每个村庄相邻的村庄数不超过 25；
90%的数据中，每个村庄相邻的村庄数不超过 150；
100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

传送门：

https://www.lydsy.com/JudgeOnline/problem.php?id=1912

思路：

首先考虑不加边走过的距离显然是$ 2(n-1) $。

1.$ k=1 $，这种情况明显是在最长路径两头加边，结果为$ 2(n-1)-d_1+1 $。

2.$ k=2 $，这种情况是在找到次长路径两头加边，结果为$ 2(n-1)-d_1+1-d_2+1 $。

不过题目要求所有边都要经过，所以计算第二种情况的$ d_2 $之前，需要在第一次求出最长路径之后，将这条路径上的所有边权变为-1。

这样做的结果是重叠的部分由只经过一次，变成经过两次。

不过为了方便第二次计算，还要在第一次求最长路径的时候，用链表记录下经过的路径。

这个路径是两条路径相交而成的，假设这两条路径的交点为$x$：一条是$ x $下面的最长路，另一条是$ x $下面的次长路(注意它也是包含了$ y $下面的最长路)，如下图

 

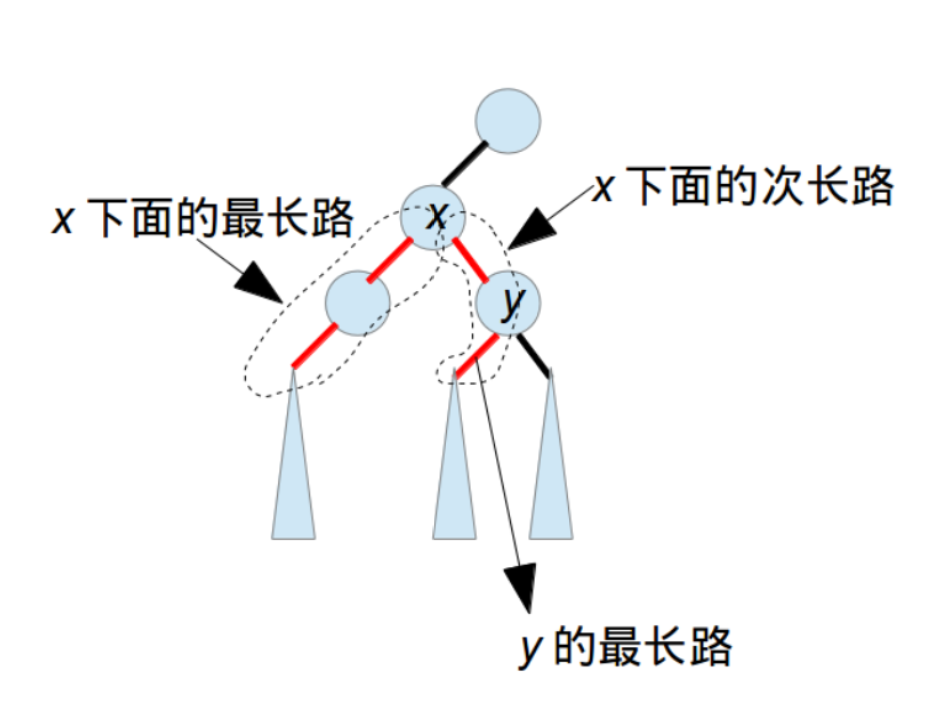
 这就是代码中开始是由$s_2[] $数组索引，最后却变成由$ s_1[]$数组索引。

代码

  1 #include<bits/stdc++.h>
  2 
  3 using namespace std;
  4 
  5 const int N = 100005;
  6 
  7 struct node
  8 {
  9     int to;
 10     int v;
 11     int nxt;
 12 };
 13 
 14 node e[N << 1];
 15 
 16 int head[N];
 17 
 18 int tot;
 19 void addedges(int u, int v)
 20 {
 21     e[++tot].to = v;
 22     e[tot].v = 1;
 23     e[tot].nxt = head[u];
 24     head[u] = tot;
 25 
 26     e[++tot].to = u;
 27     e[tot].v = 1;
 28     e[tot].nxt = head[v];
 29     head[v] = tot;
 30 }
 31 int s1[N];
 32 int s2[N];
 33 int dis;
 34 int pos;
 35 //通过找最大和次大来求直径
 36 int dfs(int x, int fa)
 37 
 38 {
 39     int fm = 0;//最大值
 40     int sm = 0;//次大值
 41 
 42     for(int i = head[x]; i; i = e[i].nxt)
 43     {
 44         int y = e[i].to;
 45         if(y == fa)
 46             continue;
 47         int v = e[i].v + dfs(y, x);
 48 
 49         if(v > fm)
 50         {
 51             sm = fm;
 52             fm = v;
 53             s2[x] = s1[x];
 54             s1[x] = i;
 55         }
 56         else if(v > sm)
 57         {
 58             sm = v;
 59             s2[x] = i;
 60         }
 61     }
 62     if(fm + sm > dis)
 63     {
 64         dis = fm + sm;
 65         pos = x;
 66     }
 67     return fm;
 68 }
 69 int main()
 70 
 71 {
 72     int n, k;
 73     scanf("%d%d", &n, &k);
 74     for(int i = 1; i < n; i++)
 75     {
 76         int a, b;
 77         scanf("%d%d", &a, &b);
 78         addedges(a, b);
 79     }
 80     int ans = 2 * (n - 1);
 81 
 82     dfs(1, 0);
 83     ans = ans - dis + 1;
 84 
 85     if(k == 2)
 86     {
 87         dis = 0;
 88         for(int i = s1[pos]; i; i = s1[e[i].to] )
 89         {
 90             e[i].v = -1;
 91         }
 92 
 93         for(int i = s2[pos]; i; i = s1[e[i].to] )//上面图片的内容
 94         {
 95             e[i].v = -1;
 96         }
 97         dfs(1, 0);
 98         ans = ans - dis + 1;
 99     }
100 
101     printf("%d\n", ans );
102 }

 

：

posted @ 2020-02-17 19:36  是妖妖灵鸭  阅读(108)  评论(0)  编辑  收藏  举报