Spark MLib：梯度下降算法实现

声明：本文参考《 大数据：Spark mlib(三) GradientDescent梯度下降算法之Spark实现》

1. 什么是梯度下降？

梯度下降法（英语：Gradient descent）是一个一阶最优化算法，通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。
先来看两个函数：
1.  拟合函数：为参数向量，h(θ)就是通过参数向量计算的值，n为参数的总个数，j代表的是一条记录里的一个参数
 
 
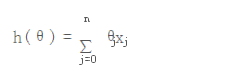
2. 损失函数：
   
 
m为训练的集合数，i代表的是一条记录，hθ(xi)代表的是第i条的h(θ)
在监督学习模型中，需要对原始的模型构建损失函数J(θ),  接着就是最小化损失函数，用以求的最优参数θ
对损失函数θ进行求偏导，获取每个θ的梯度

,

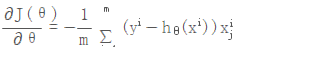
2. 梯度下降的几种方式

2.1 批量梯度下降（BGD）

在前面的方式，我们采样部分数据，就称为批量梯度下降
在公式：

中我们会发现随着计算θ的梯度下降，需要计算所有的采样数据m，计算量会比较大。

2.2  随机梯度下降 (SGD)

在上面2.1的批量梯度下降，采样的是批量数据，那么随机采样一个数据，进行θ梯度下降，就被称为随机梯度下降。

损失函数：

 

那么单样本的损失函数：m=1 的情况：

 

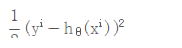
对单样本的损失函数进行求偏导，计算梯度下降

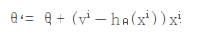
为了控制梯度下降的速度，引入步长

3. Spark 实现的梯度下降

spark实现在mlib库下org.apache.spark.mllib.optimization.GradientDescent类中

3.1 随机梯度？

看函数名字叫做SGD，会以为是随机梯度下降，实际上Spark里实现的是随机批量的梯度下降
我们去看梯度下降的批量算法公式：
这个公式可以拆分成两部分
  1. 计算数据的梯度
  2. 根据梯度计算新的权重

3.2 计算梯度

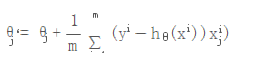
在前面的章节里描述过随机和批量的主要区别就是在计算梯度上，随机采样只是随机采用单一样本，而批量采样如果采样所有数据，涉及到采样的样本、计算量大的问题，Spark采用了择中的策略，随机采样部分数据
  • 先随机采样部分数据
data.sample(false, miniBatchFraction, 42 + i)
  • 对部分数据样本进行聚合计算
treeAggregate((BDV.zeros[Double](n), 0.0, 0L))(  
          seqOp = (c, v) => {  
            // c: (grad, loss, count), v: (label, features)  
            val l = gradient.compute(v._2, v._1, bcWeights.value, Vectors.fromBreeze(c._1))  
            (c._1, c._2 + l, c._3 + 1)  
          },  
          combOp = (c1, c2) => {  
            // c: (grad, loss, count)  
            (c1._1 += c2._1, c1._2 + c2._2, c1._3 + c2._3)  
          })
使用treeAggregate，而没有使用Aggregate，是因为treeAggregate比aggregate更高效，combOp会在executor上执行
在聚合计算的seqOp里我们看到了gradient.compute来计算梯度

3.2.1 Spark 提供的计算梯度的方式

  • LeastSquaresGradient 梯度，主要用于线型回归
  • HingeGradient 梯度，用于SVM分类
  • LogisticGradient 梯度，用于逻辑回归
前面章节里描述的就是基于线性回归模型的计算梯度的方式，也就是如下公式：

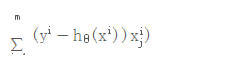
3.3 跟新权重theta θ

在梯度下降计算中，计算新的theta（也叫权重的更新），更新的算法由你采用的模型来决定

val update = updater.compute(  
          weights, Vectors.fromBreeze(gradientSum / miniBatchSize.toDouble),  
          stepSize, i, regParam)
目前Spark默认提供了3种算法跟新theta
  • SimpleUpdater  
  • L1Updater   
  • SquaredL2Updater

3.3.1 SimpleUpdater

以SimpleUpdater来说：
SimpleUpdater extends Updater {  
  override def compute(  
      weightsOld: Vector,  
      gradient: Vector,  
      stepSize: Double,  
      iter: Int,  
      regParam: Double): (Vector, Double) = {  
    val thisIterStepSize = stepSize / math.sqrt(iter)  
    val brzWeights: BV[Double] = weightsOld.asBreeze.toDenseVector  
    brzAxpy(-thisIterStepSize, gradient.asBreeze, brzWeights)  
  
    (Vectors.fromBreeze(brzWeights), 0)  
  }  
}

也就是上面提到的公式：

相对来说simpleupdater算法比较简单，在这里没有使用正则参数regParam，只是使用了每个迭代的步长作为相同的因子，计算每一个theta，也就是权重。
迭代的步长=总步长/math.sqrt(迭代的次数)

3.3.2 其它的正则参数化算法

L1Updater： 正则化算法
  1. 和SimpleUpdater一样更新权重
  2. 将正则化参数乘以迭代步长的到比较参数：shrinkage
  3. 如果权重大于shrinkage，设置权重-shrinkage
  4. 如果权重小于-shrinkage，设置权重+shrinkage
  5. 其它的，设置权重为0
SquaredL2Updater：正则化算法
w' = w - thisIterStepSize * (gradient + regParam * w)

和SimpleUpdater比较，补偿了regParam*w ,这也是逻辑回归所采用的梯度下降算法的更新算法

4.  梯度下降收敛条件

如何判定梯度下降权重值收敛不在需要计算，通常会有两个约束条件
  • 迭代次数，当达到一定的迭代次数后，权重的值会被收敛到极值点，并且不会受到次数的影响
  • 筏值：当两次迭代的权重之间的差小于指定的筏值的时候，就认为已经收敛
在Spark里使用了L2范数来比较筏值
private def isConverged(  
    previousWeights: Vector,  
    currentWeights: Vector,  
    convergenceTol: Double): Boolean = {  
  // To compare with convergence tolerance.  
  val previousBDV = previousWeights.asBreeze.toDenseVector  
  val currentBDV = currentWeights.asBreeze.toDenseVector  
  
  // This represents the difference of updated weights in the iteration.  
  val solutionVecDiff: Double = norm(previousBDV - currentBDV)  
  
  solutionVecDiff < convergenceTol * Math.max(norm(currentBDV), 1.0)  
}

当前后权重的差的L2，小于筏值*当前权重的L2和1的最大值，就认为下降结束。

5.  Spark实现梯度下降的实现示例：

import org.apache.spark.sql.SparkSession
import org.apache.spark.{SparkConf}
import org.apache.spark.mllib.linalg.{Vectors}
import org.apache.spark.mllib.optimization._

object SGDExample {
  def main(args: Array[String]): Unit = {
    val conf = new SparkConf()
    conf.set("spark.sql.broadcastTimeout", "10000")
    conf.set("fs.defaultFS", "hdfs://abccluster")
    val spark = SparkSession.builder().appName("hz_mlib").config(conf).enableHiveSupport().getOrCreate()


    /**
      * 这里以简单的y=3*x+1为例来简单使用一下
      * 测试数据就随意
      * 1 0 1
      * 7 2 1
      * 10 3 1
      * 4 1 1
      * 19 6 1
      **/
    val list = List[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]](
      Tuple2(1d, Vectors.dense(0.0d, 1d)),
      Tuple2(7d, Vectors.dense(2.0d, 1d)),
      Tuple2(10d, Vectors.dense(3.0d, 1d)),
      Tuple2(4d, Vectors.dense(1.0d, 1d)),
      Tuple2(19d, Vectors.dense(6.0d, 1d))
    )

    val data: org.apache.spark.rdd.RDD[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]] = spark.sparkContext.parallelize(list)

    /**
      * 而具体的实现梯度有
      * LogisticGradient
      * LeastSquaresGradient
      * HingeGradient
      * 对于更新也是三种实现
      * SimpleUpdater
      * L1Updater
      * SquaredL2Updater
      **/
    var gradient = new LeastSquaresGradient()
    var updater = new L1Updater()

    /**
      * GradientDescent parameters default initialize values:
      * private var stepSize: Double = 1.0
      * private var numIterations: Int = 100
      * private var regParam: Double = 0.0
      * private var miniBatchFraction: Double = 1.0
      * private var convergenceTol: Double = 0.001
      */
    var stepSize = 1.0
    var numIterations = 100
    var regParam: Double = 0.0
    var miniBatchFraction = 1.0
    var initialWeights: org.apache.spark.mllib.linalg.Vector = Vectors.dense(0d, 0d)
    var convergenceTol = 0.001
    val (weights, _) = GradientDescent.runMiniBatchSGD(
      data: org.apache.spark.rdd.RDD[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]],
      gradient: org.apache.spark.mllib.optimization.Gradient,
      updater: org.apache.spark.mllib.optimization.Updater,
      stepSize: scala.Double,
      numIterations: scala.Int,
      regParam: scala.Double,
      miniBatchFraction: scala.Double,
      initialWeights: org.apache.spark.mllib.linalg.Vector,
      convergenceTol: scala.Double)

    println(weights)


    spark.stop()
  }
}

输出测试结果：

scala> import org.apache.spark.mllib.linalg.{Vectors}
import org.apache.spark.mllib.linalg.Vectors

scala> import org.apache.spark.mllib.optimization._
import org.apache.spark.mllib.optimization._

scala>  /**
     |       * 这里以简单的y=3*x+1为例来简单使用一下
     |       * 测试数据就随意
     |       * 1 0 1
     |       * 7 2 1
     |       * 10 3 1
     |       * 4 1 1
     |       * 19 6 1
     |       **/
     |     val list = List[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]](
     |       Tuple2(1d, Vectors.dense(0.0d, 1d)),
     |       Tuple2(7d, Vectors.dense(2.0d, 1d)),
     |       Tuple2(10d, Vectors.dense(3.0d, 1d)),
     |       Tuple2(4d, Vectors.dense(1.0d, 1d)),
     |       Tuple2(19d, Vectors.dense(6.0d, 1d))
     |     )
list: List[(Double, org.apache.spark.mllib.linalg.Vector)] = List((1.0,[0.0,1.0]), (7.0,[2.0,1.0]), (10.0,[3.0,1.0]), (4.0,[1.0,1.0]), (19.0,[6.0,1.0]))

scala> 

scala>     val data: org.apache.spark.rdd.RDD[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]] = spark.sparkContext.parallelize(list)
data: org.apache.spark.rdd.RDD[(Double, org.apache.spark.mllib.linalg.Vector)] = ParallelCollectionRDD[11460] at parallelize at <console>:37

scala> 

scala>     /**
     |       * 而具体的实现梯度有
     |       * LogisticGradient
     |       * LeastSquaresGradient
     |       * HingeGradient
     |       * 对于更新也是三种实现
     |       * SimpleUpdater
     |       * L1Updater
     |       * SquaredL2Updater
     |       **/
     |     var gradient = new LeastSquaresGradient()
gradient: org.apache.spark.mllib.optimization.LeastSquaresGradient = org.apache.spark.mllib.optimization.LeastSquaresGradient@7adb7d5b

scala>     var updater = new L1Updater()
updater: org.apache.spark.mllib.optimization.L1Updater = org.apache.spark.mllib.optimization.L1Updater@33e6a825

scala> 

scala>     /**
     |       * GradientDescent parameters default initialize values:
     |       * private var stepSize: Double = 1.0
     |       * private var numIterations: Int = 100
     |       * private var regParam: Double = 0.0
     |       * private var miniBatchFraction: Double = 1.0
     |       * private var convergenceTol: Double = 0.001
     |       */
     |     var stepSize = 1.0
stepSize: Double = 1.0

scala>     var numIterations = 100
numIterations: Int = 100

scala>     var regParam: Double = 0.0
regParam: Double = 0.0

scala>     var miniBatchFraction = 1.0
miniBatchFraction: Double = 1.0

scala>     var initialWeights: org.apache.spark.mllib.linalg.Vector = Vectors.dense(0d, 0d)
initialWeights: org.apache.spark.mllib.linalg.Vector = [0.0,0.0]

scala>     var convergenceTol = 0.001
convergenceTol: Double = 0.001

scala>     val (weights, _) = GradientDescent.runMiniBatchSGD(
     |       data: org.apache.spark.rdd.RDD[scala.Tuple2[scala.Double, org.apache.spark.mllib.linalg.Vector]],
     |       gradient: org.apache.spark.mllib.optimization.Gradient,
     |       updater: org.apache.spark.mllib.optimization.Updater,
     |       stepSize: scala.Double,
     |       numIterations: scala.Int,
     |       regParam: scala.Double,
     |       miniBatchFraction: scala.Double,
     |       initialWeights: org.apache.spark.mllib.linalg.Vector,
     |       convergenceTol: scala.Double)
weights: org.apache.spark.mllib.linalg.Vector = [3.000248212261404,0.9997330919125574]

scala> 

scala>     println(weights)
[3.000248212261404,0.9997330919125574]

样例实现：参考《夜明的孤行灯 -》Spark中的梯度下降 -》 https://www.huangyunkun.com/2015/05/27/spark-gradient-descent/#comment-9317》

 

posted @ 2018-03-31 14:28  cctext  阅读(1098)  评论(0)  编辑  收藏  举报