含有+-*/()的表达式求值
对于表达式,有常用的几种形式:
- 中缀表达式(Infix expression):操作符位于两个操作数中间,算术表达式的常规表示法。需要用括号和优先规则排除多义性。(这也正是编写程序的麻烦点,需要制定完整的优先规则)(A+B)*C-D/(E+F)
- 后缀表达式(Postfix expression),逆波兰表示法,操作符位于操作数后面。这种方法使表达式求值很方便。AB+C*DEF+/- 。
- 前缀表达式(Prefix expression):也叫波兰表示法,操作符写在操作数的前面。这种方法常用于编译器设计方面。-*+ABC/D+EF
(在这里,不考虑前缀表示法)
为了简化问题,关注算法,本文的讨论基于以下三点:
- 只考虑 + - * / ( ) 这几个基本运算符。
- 运算数只考虑 0-9,这10个简单的数,方便从string中取出来。
- 输入的表达式没有语法错误。
现在先不考虑求值,先来考虑一个有趣的东西:表达式树
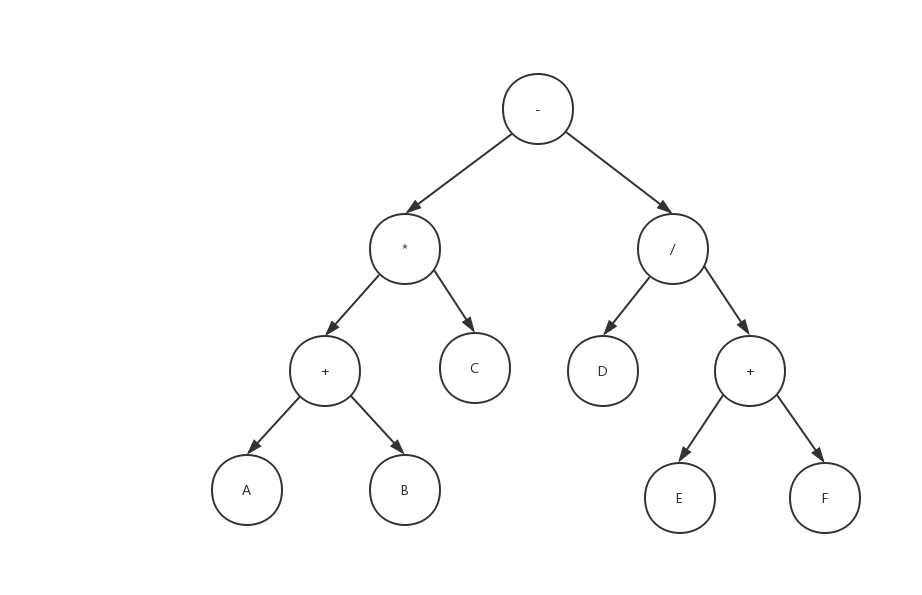
(A+B)*C-D/(E+F)的表达式树
- 非叶子结点都是运算符,数值都在叶子结点。
- 在上面我忽略了一种情况:“-” 作为单目运算符的情况 (-a):可以让a作为右结点,左结点为空; 也可以让左结点为0;
- 从递归来看:一个子树能够得到一个值(返回值),该子树得到的值通过根结点的符号,左子树的值和右子树的值进行运算得到(递归实体);如果该结点为叶子结点,那么直接返回值就行了。(求值的递归公式)
- 在表达式树中,不需要加括号,因为括号所表示的优先级以及被树的结构包含了。 (自底向上计算,同一层的位于同一结点下的数值才能够运算)
- 给出表达式树,要求表达式:先序遍历对应前缀表达式,中序遍历对应中缀表达式(需要看情况加括号),后序遍历对应后缀表达式。
先考虑最简单的表示法:如果给出后缀表达式,AB+C*DEF+/-
算法思路:
- 给出后缀表达式S;建立一个栈,数字栈stack1。
- 循环读入表达式的每一个单元:
- 如果读入的字符是数字,那么入栈;
- 如果读入的字符是符号,那么弹栈两次,后弹出来的记为n1,先弹出来的记为n2;那么结果就为n1-n2;然后将结果入栈。
- 最后在栈中会得到最终结果。
因为后缀表达式不需要进行优先级规则的判断,因此,处理规则异常简单,只需要直接判断就行了。
如果给出的是中缀表达式,(A+B)*C-D/(E+F):



