字符串匹配算法
问题大致含义:给出两个字符串s1、s2,判断s2是否为s1的子串。
普通匹配算法:
时间复杂度:O(mn),m,n是两个串的长度。
1 /* 字符串下标始于 0 */ 2 int NaiveStringSearch(string S, string P) 3 { 4 int i = 0; // S 的下标 5 int j = 0; // P 的下标 6 int s_len = S.size(); 7 int p_len = P.size(); 8 9 while (i < s_len && j < p_len) 10 { 11 if (S[i] == P[j]) // 若相等,都前进一步 12 { 13 i++; 14 j++; 15 } 16 else // 不相等 17 { 18 i = i - j + 1; 19 j = 0; 20 } 21 } 22 23 if (j == p_len) // 匹配成功 24 return i - j; 25 26 return -1; 27 }
KMP算法:
算法核心:当算法匹配成功的时候与普通的字符串匹配算法并没有太大的不同,都是比较下一个元素;但是在匹配失败的时候,利用某些信息来减少一些不必要的匹配。
next数组:
- next数组是KMP的核心,当匹配失败时,通过next数组的意义能够减少不必要的匹配。
- next数组的含义:对于一个字符串S,其长度为len(S),那么next的下标范围为:0~len(S)-1,对于i∈[0,len(S)-1],next[i]:使子串S[0:i]中形成前缀S[0:k]和后缀S[i-k:i]相同的最大k值(k一定小于i,当没有一个能匹配,取-1)。
- next数组的意义:对于S,给出了所有S[0:i]的子串最长的前缀与后缀相同的位置。(字符串匹配的目的是实现所有的相同,所有相同必定是部分相同的子集,通过next数组跳入下一个可能匹配的位置) (核心:等价代换;部分与整体的关系)
用一个例子来解释next[i]: S="ababaab" len(S)=7 (下面所用的符号与上面说明对应)
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| next[i] | -1 | -1 | 0 | 1 | 2 | 0 | -1 |
- i=0时,默认为-1;(只有一个元素,S[0])
- i=1时,S[0:1]="ab",next[i]=-1,因为k=0时,S[0:0]="a",S[1:1]="b",不匹配,k必须小于i。
- i=2时,S[0:2]="aba",next[i]=0,因为k=0时,S[0:0]="a",S[2:2]=“a”,匹配; k=1时,S[0:1]="ab",S[1:2]="ba",不匹配。
- i=3时,S[0:3]="abab",next[i]=1。
- i=4,5,6::略
KMP算法:
- 注意:在匹配失败的时候如何利用next数组,以及i,j如何变化。
S1="abababaabc" S2="ababaab",判断S2是否为S1的子串。
- 建立S2的next数组;
- 用i指向S1欲匹配的字符,用j指向S2已匹配的字符;i=0,j=-1;
- 用S1[i]与S2[j+1]进行匹配:
- i∈[0,4],是匹配成功的,这时候只需要i++,j++; 最后到达i=5,j=4;(匹配成功情况)
- 因为S1[i]="b",S2[j+1]="a",因此不匹配; 关键点来了,那么用什么元素进行再次比较呢? (图1) (匹配失败情况) 此时S1[0:4]=S2[0:4], 根据next数组,next[j]=2(说明S2[0:2]=S2[2:4] ) S2[2:4]=S1[2:4], 经过等价代换 ,可以发现:S2[0:2]=S1[2:4]; 同时令j=next[j],在此时再比较S1[i]与S2[j+1],看是否相等(i=5,j=2);这时候发现相等了,因此按照成功时候进行匹配。
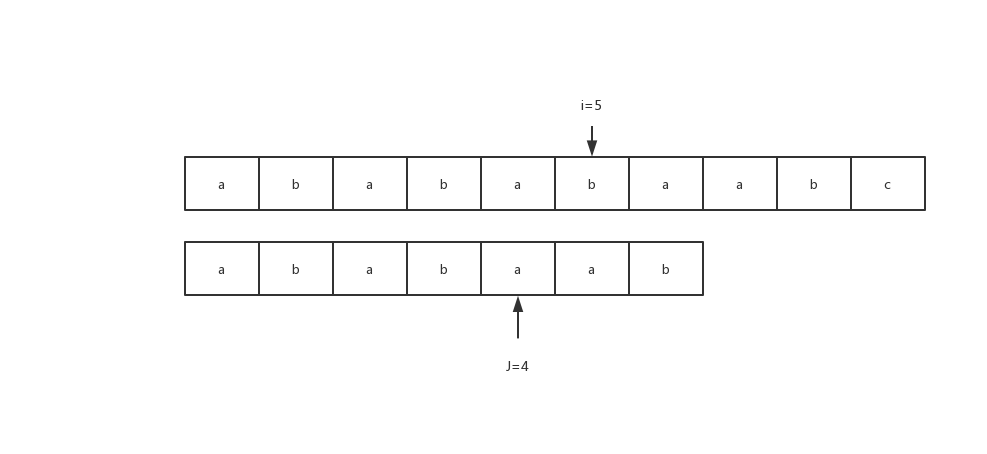 图1
图1

图2
算法步骤综述:(用数学关系完整地阐述一遍) S1:被匹配串, S2:匹配串
- 用i指向S1欲匹配的字符,用j指向S2已匹配的字符;i=0,j=-1; 建立S2的next数组。
- 循环结束条件:当j=len(S2)-1 or i=len(S1) ; 如果j=len(S2)-1,那么匹配成功; 否则,匹配失败
- 循环过程:
- 如果S1[i]=S2[j+1],那么匹配成功,i++,j++;
- 如果S1[i]!=S2[j+1],那么匹配失败,j=next[j],循环判断S1[i]与S2[j+1]的关系: 如果j=-1,并且匹配失败,那么i++;继续沿着该循环过程循环。
next数组的实现:
- 很容易想到,next数组也能够通过暴力求解:当然这个效率就很低了。
1 next[0]=-1; 2 3 for(int i=1;i<len(S);i++){ 4 int j; 5 for(j=i-1;j>=0;j--){ 6 //判断 子串[0:j]和[len(S)-1-j,len(S)-1]是否相等;当相等的时候,break; 7 } 8 next[i]=j; 9 }
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| next[i] | -1 | -1 | 0 | 1 | 2 | 0 | -1 |
- 改进实现:对于当前 i,考虑next[i]与next[0]~next[i-1]的关系:以S="ababaab"为例子
- 初始值:next[0]=-1,i=1。
- 考虑i=4和i=5的实现:i=4能够体现出匹配成功的情况,i=5能够体现出匹配失败的情况 (next表见上方)
- 对于i=4,next[i-1]=1; 这时候考虑S[i]="a"和S[next[i-1]+1]="a"的关系,相等,那么next[i]=next[i-1]+1;
- 对于i=5,next[i-1]=2; 这时候考虑S[i]="a"和S[next[i-1]+1]="b"的关系,不相等,那么匹配失败; 注意此刻条件,S[0:next[i-1]]和S[i-next[i-1]-1:i-1]是相同的,只是S[i]="a"和S[next[i-1]+1]不同,对于串的匹配,所有匹配必是部分匹配的子集,那么考虑前缀S[0:next[i-1]],求出得到next[next[i-1]]=0,判断S[0+1]="b"与S[i]="a"的关系,发现还是不相同; 那么继续失败的模式,next[next[next[i-1]]]=-1,判断S[-1+1]="a"与S[i]="a"的关系,发现相同,那么令next[i]=next[0]+1;
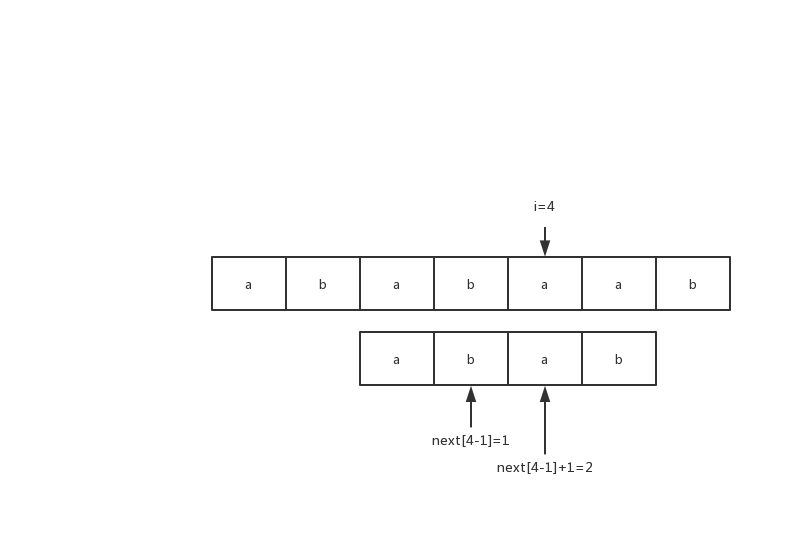
图3)i=4时,S[i]与S[next[i-1]+1]
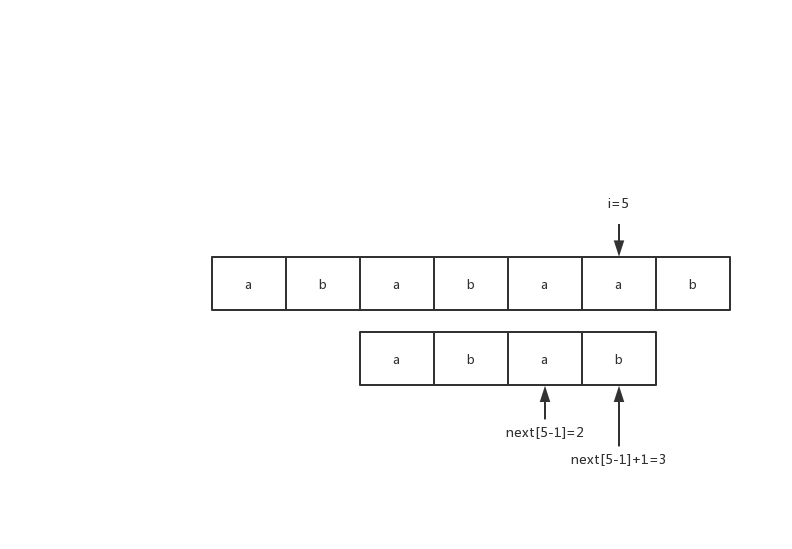
图4) 第一次匹配失败 S[5]与S[next[4]+1]
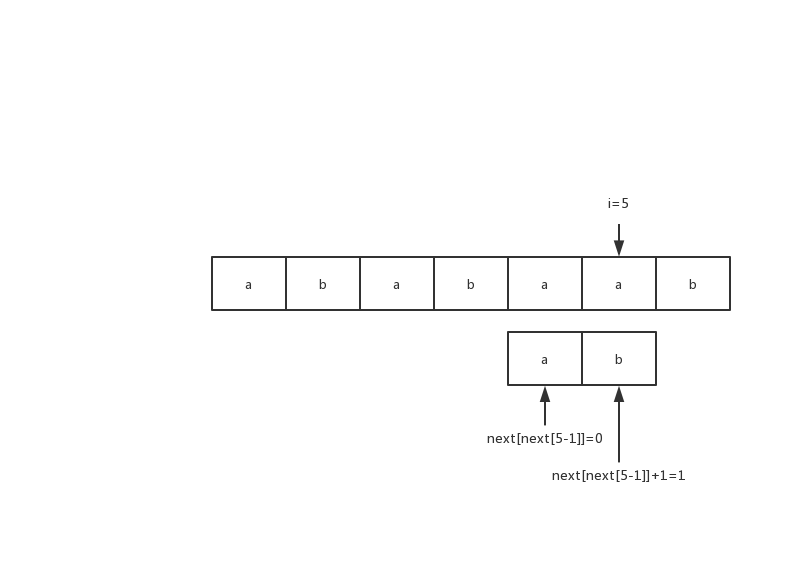
图5)第二次匹配失败 S[5]与S[1]
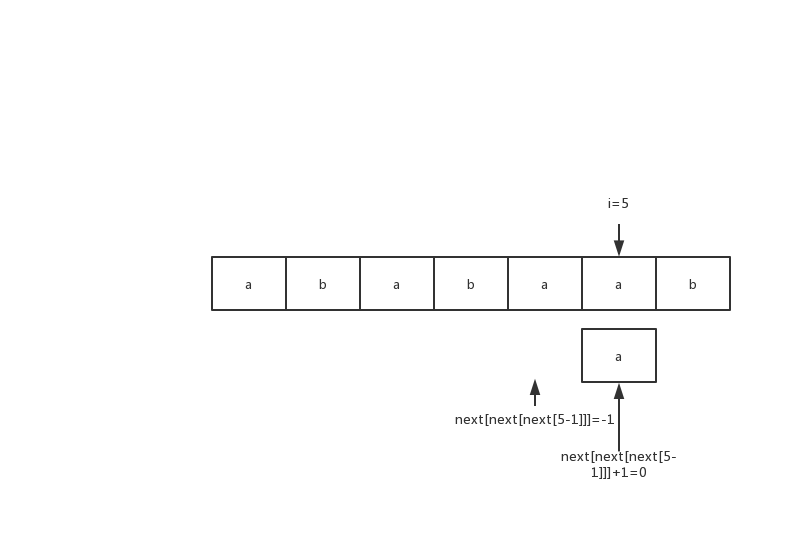
图6) S[5]与S[0]匹配成功 (如果这次再匹配失败,那么i++,next[5]=-1)
-
究其本质:发现next数组的实现过程其实是对于每一个S[0:i]和自身某些前缀的KMP匹配。对于S[0:i],已知next[0]~next[i-1],next[0]~next[i-1]提供了前缀和后缀的一致信息,我们只要保证S[i]和S[next[i-1]+1]相等就行。
1 int* getNext(char* S,int length){ 2 int* next=(int*)malloc(sizeof(int)*length); 3 next[0]=-1; 4 // next[i] 5 for(int i=1;i<length;i++){ 6 int j=next[i-1]; 7 while(S[i]!=S[j+1]){ 8 if(j==-1){ // 无匹配项 9 break; 10 } 11 else{ 12 j=next[j]; 13 } 14 } 15 if(S[i]==S[j+1]){ 16 j++; 17 } 18 next[i]=j; 19 }
20 return next; 21 }
KMP算法的实现:
bool KMP(char* S1,char* S2){ int n=strlen(S1),m=strlen(S2); getNext(S2,m); // 获得S2的next数组 int j=-1; // 记录S2已匹配串位置 int i=0; // 记录S1欲匹配位置 while(i<n && j<m-1){ // 匹配成功 if(S1[i]==S2[j+1]){ i++; j++; } else{ // 匹配失败,并且j=-1 if(j==-1){ i++; } else{ j=next[j]; } } } if(j==m-1){ return true; } else{ return false; } }





