子集（力扣第78题）

题目：

　　给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

　　说明：解集不能包含重复的子集。

示例：

输入: nums = [1,2,3]
输出:
[
[3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

分析：

　　子集的大小可以是从0到nums.length，也就是可以为空集，也可以和原始集合一模一样。此题还是采用回溯的方法进行求解，只不过，需要搞清楚，集合内部是不能有重复的元素存在的，每个子集所包含的元素（不考虑顺序）也是不能相同的。

　　按照一般的解法时，可以以搜索路径长度作为遍历的对象，搜索路径长度分别从0到nums.length，依次求出对应的搜索结果集合，代码实现如下：

  private List<List<Integer>> resList;

    public List<List<Integer>> subsets(int[] nums) {

        if (nums == null || nums.length == 0){
            return new ArrayList<>();
        }

        resList = new ArrayList<>();
        resList.add(new ArrayList<>());
        List<Integer> curlist = new ArrayList<>();

        for (int i = 1; i <= nums.length; i++) {
            findSubsets(nums,curlist,0,i);
        }

        return resList;
    }

    private void findSubsets(int[] nums, List<Integer> curlist, int s,int curlen) {

        if (curlist.size() == curlen){

            resList.add(new ArrayList<>(curlist));
            return;
        }

        for (int j = s; j < nums.length; j++) {

            curlist.add(nums[j]);
            findSubsets(nums,curlist,j+1,curlen);
            curlist.remove(curlist.size()-1);
        }
    }

　　上面的代码虽然解决了问题，但是由于需要挨个遍历搜索路径的长度，所以效率十分低下，因此为了提高程序的性能，我对上面的代码进行了优化。我们知道，这些子集的元素组合，数量较少的组合往往可以看作是元素数量较多的组合在相同搜索路径上的一部分，准确的说是前一部分。在整个搜索结果中，搜索路径长度最长的情况就是路径上包含了数组中的所有元素，那么我们回溯的意义是什么呢？

　　就是当到达某个点的时候，此时无法继续向下了，那我们就返回上一层搜索的点，然后基于返回的上一层的点，去寻找其他可走的路径，也就是回溯寻找到的新路径，之所以新，在于从某个点开始，路径分开了，这个点之前的路径节点都是相同的。

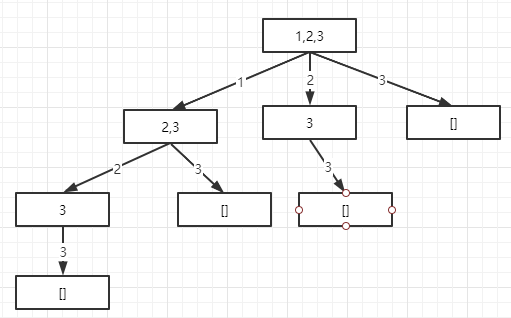
　　我们的做法是，从开始遍历的点开始，每次前进一步，就记录一个搜索结果，存入结果集合中。但是中间可能会产生重复的，比如如下图所示，最左边的路径，如果3也遍历完了，此时结果集中的集合是[1],[1,2],[1,2,3]；然后开始向上回溯，根据回溯的特点，此时暂存元素的集合要删除3，此时只剩下[1,2]，而这时按照一贯的想法是在2这个点处，执行下一轮for循环，那么遍历访问的还是3，那么3就又走了一遍，所就产生了重复。那么如何解决重复的问题呢？

　　前面说过，根据回溯和深度遍历的规律，上面那种重复的原因在于，它们往往都是在前一部分是相同的路径，然后在某个点处分开了，比如当在2这个点处，先走的是2+1这个，然后走完了回溯，此时2还在暂存元素列表，然后此时又走向了3，只不过不是基于2为父节点的搜索，那么就产生了重复。所以解决办法就是采用一个变量，去记录某次遍历下，上一次的访问元素，比如访问完3，回溯到了2，那么上一次访问的元素就是3，而此时再走向3的时候就会先和那个变量值就行比较，如果相等就直接跳过。

 

 

private List<List<Integer>> resList;

    public List<List<Integer>> subsets(int[] nums) {

        if (nums == null || nums.length == 0){
            return new ArrayList<>();
        }

        resList = new ArrayList<>();
        resList.add(new ArrayList<>());
        List<Integer> curlist = new ArrayList<>();

        findSubsets(nums,curlist,0);

        return resList;
    }
    int lastnum = Integer.MIN_VALUE;
    private void findSubsets(int[] nums, List<Integer> curlist, int s) {

        if (curlist.size() == nums.length){
            return;
        }

        for (int j = s; j < nums.length; j++) {

            if (nums[j] != lastnum){
                curlist.add(nums[j]);
                resList.add(new ArrayList<>(curlist));
                findSubsets(nums,curlist,j+1);
                lastnum = curlist.get(curlist.size()-1);
                curlist.remove(curlist.size()-1);
            }
        }
    }