组合（力扣第77题）

题目：

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例：

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

分析：

　　这是一个组合问题，所以结果顺序不同并不会影响结果，不同的结果组合中构成的元素成分是一样的那么这些结果组合就是相同的，同时题目也规定了搜索路径的长度，搜索的长度等于规定长度，那么搜索随即终止。那么首先，想到的就是利用DFS和回溯的思想解决这个问题。然后通过分析具体的过程，进行了剪枝优化，从而提高了程序的运行效率。那么现在分别讲解一下两种解法：

解法一：回溯

　　假设，n=4,k=2；那么我们开始详细说一下求解的过程：

　　从1开始搜索，其搜索的过程如图所示：

 

 

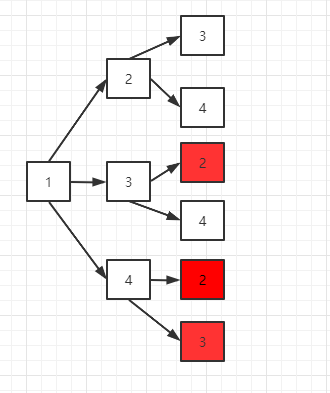
　　可以看出标出红色的部分是重复的搜索，即按照1为出发点，红色部分为终点，搜索路径上构成的组合是已经存在的，那么就需要如何将这些重复的去掉呢？通过规律可以发现，只要保证在搜索过程中同一条搜索路径下前一个结点的值小于后一个结点的值时，就不会造成重复的组合出现。

 

 代码实现：

    private List<List<Integer>> resList;

    public List<List<Integer>> combine(int n, int k) {

        boolean[] isVisited = new boolean[n];

        resList = new ArrayList<>();
        List<Integer> curRes = new ArrayList<>();
        findResByDFS(curRes,k,1,n);

        return resList;
    }

    private void findResByDFS(List<Integer> curRes,int k,int s,int n){

        if (curRes.size() == k){
            resList.add(new ArrayList<>(curRes));
            return;
        }

        for (int i = s; i <= n; i++) {

            curRes.add(i);
            findResByDFS(curRes,k,i+1,n);
            curRes.remove(curRes.size()-1);
        }
    }

解法二：回溯+剪枝（优化版本）

　　上面的代码性能不够好，所以需要进行优化，我们通过一个例子全面分析整个过程，假设n=4，k=3，其求出所有组合的过程如下：

 

 

 

 　　k的值是我们要求的组合的元素个数，n时我们搜索时可选的范围，即1~n。我们以curlen作为当前搜索路径的长度，max_i表示能够得出最终路径的最大元素值，remain表示获得指定大小的组合还需要取出的元素个数，分析整个过程：

　　　　选定0个数时，curlen=0,n=4,k=3,max_i=2, remian=3

　　　　选定1个数时，curlen=1,n=4,k=3,max_i=3, remain=2

　　　　选定2个数时，curlen=2,n=4,k=3,max_i=4, remain=1

　　通过观察，可以发现这些值之间的关系，remain+max_i - 1 = n;进行一些变换可以得到，max_i = n - (k-curlen) + 1;remain = k - curlen;

　　为何会有如此的情况呢，我们观察上面的运算过程图，在某一层中，其向下要进行搜索的时候，要选出下一个要搜索的数，要想保证选择某个数作为当前层的下一步要搜索的数使得最终能够产生组合结果，就必须保证选择这个数字以后，在整条路径的中可选的元素个数不能小于结果组合还需要的元素个数。即：n-i+1 >= k-curlen

　　就比如最开始的时候，为了选择4作为下一步搜索数，最终没有组合结果。就是因为选择4作为下一步搜索数以后，构成结果组合一共需要2个数，而此时，选择4的这条路径，除了4以外已经没有可选的数了，显然小于2，所以最终是没有结果的。可以看出我们就是在优化，选择下一步搜索数时，进行循环判断的范围。

代码实现：

    private List<List<Integer>> resList;

    public List<List<Integer>> combine(int n, int k) {

        boolean[] isVisited = new boolean[n];

        resList = new ArrayList<>();
        List<Integer> curRes = new ArrayList<>();
        findResByDFS(curRes,k,1,n);

        return resList;
    }

    private void findResByDFS(List<Integer> curRes,int k,int s,int n){

        if (curRes.size() == k){
            resList.add(new ArrayList<>(curRes));
            return;
        }

        for (int i = s; i <= n-(k-curRes.size())+1; i++) {

            curRes.add(i);
            findResByDFS(curRes,k,i+1,n);
            curRes.remove(curRes.size()-1);
        }
    }