有效的完全平方数（力扣第367题）

题目：

　　给定一个正整数 num，编写一个函数，如果 num 是一个完全平方数，则返回 True，否则返回 False。

　　说明：不要使用任何内置的库函数，如 sqrt。

分析：

　　这个题是一个简单题，通过循环能够很容易的做出来，但是如果只用简单的循环去判断是否是完全平方数会超出时间限制，也就是说这样的方式性能太低了。所以只能通过其他方式让程序的运行更为快捷。

方法一：暴力循环，lue

public boolean isPerfectSquare(int num) {
        if (num == 1){
            return true;
        }
        int flag = 0;
        int i = 2;
        while (i <= (num/2)){

            if (i * i == num){
                flag = 1;
            }else if (i * i > num){
                break;
            }
            i++;
        }
        if (flag == 1){
            return true;
        }else {
            return false;
        }
}

方法二：等差序列

　　分析一下，完全平方数：0,1,4,9,16,25,36，……    它们之间的差值依次是1,3,5,7,9,11；这是一个等差数列，用一个表格更加清晰的表示一下它们递进的过程：

平方数	差值
0	1
1	3
4	5
9	7
16	9
25	11
……

　　可以看出，从第一个完全平方数0开始，它加上第一个差值1，就是下一个完全平方数，依次类推，这些完全平方数之间的差值是一个递增的等差数列，而且会发现第i个完全平方数，其实就是前i-1个差值相加之后的结果，比如第3个完全平方数是4，那么前两个差值相加1+3就等于4。

　　根据这个规律我们可以让num依次减去差值，最后判断num是否等于0，等于0说明是完全平方数，不等于0，说明不是。差值初始值是1，每次递增2；

public boolean isPerfectSquare4(int num) {
        if (num < 2){
            return true;
        }
        int sumnum = 1;

        while (num > 0){
            num -= sumnum;
            sumnum += 2;
        }
        return (num == 0);
}

方法三：二分查找

　　分析可以，一个大于2的完全平方数，其因子一定小于等于他的一半，那我们就设置两个指针l和r，分别指向第一个数和num/2，然后判断mid = (l + r) /2 的平方是否和num相等，如果不等那就再具体分析，大于num就减少右指针，r = mid - 1，小于num就增加左指针，l = mid + 1,遍历的整个过程如果没有mid平方值和num相等的情况，那就说明不是完全平方。

public boolean isPerfectSquare3(int num) {
        if (num == 1){
            return true;
        }
        long r = num /2;
        long l = 2;

        while (l <= r){
            long mid = (r - l) /2 + l;
            if (mid * mid == num){
                return true;
            }else if (mid * mid > num){
                r = mid - 1;
            }else {
                l = mid + 1;
            }
        }
        return false;
}

方法四：牛顿迭代法

　　设置一个函数f(x) = x²-num，当f(x) = x²-num = 0时，x这个根如何求？牛顿迭代法，就是不断用这个二次函数的切线，不断去逼近二次函数和x轴的交点。具体做法就是，先寻找一点x_{k ,}求出对应的函数值f(x_k),然后求出在这一点处的二次函数的切线，这个是很好求，已经知道一个点(x_k,f(x_k)),然后对二次函数求导，再将x_k这个值带入可以求出切线斜率，就可以求出这个切线的函数表达式了，然后令这个函数表达式等于0，求出切线和x轴交点，判断是否等于二次函数和x轴交点，如果不等，就继续上述操作，不断逼近。

 

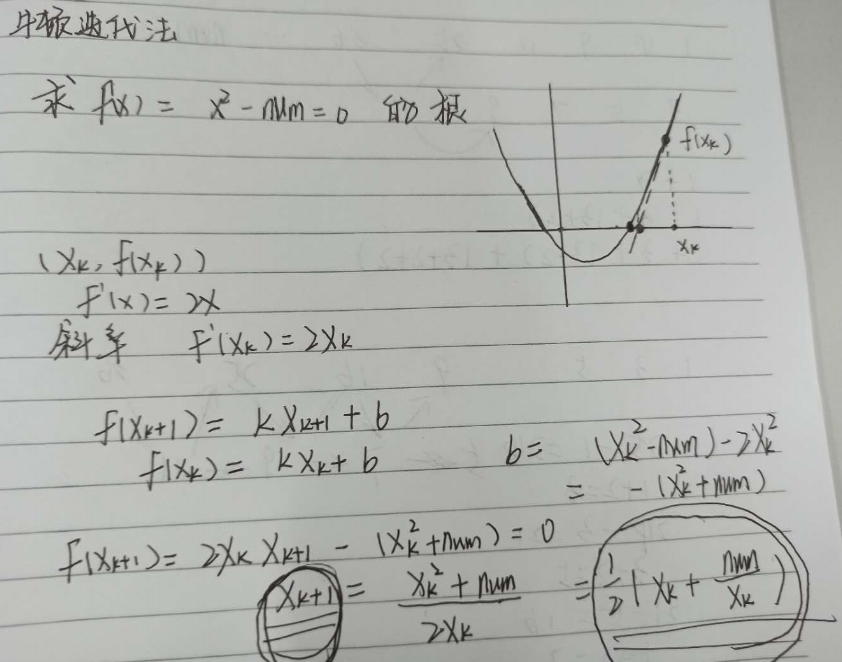
 　　利用这一原理，我们就可以完成对一个数是否是完全平方数进行判断。设近似值为x，初始值设置为num/2，循环判断x*x是否大于num，如果是那就不断使用牛顿迭代法缩小近似值。具体的代码实现如下：

public boolean isPerfectSquare2(int num) {
        if (num == 1){
            return true;
        }
        long x = num / 2;
        while (x * x > num){

            x = (x + num / x)/2;
        }

        return (x * x == num);
}

参考自：

cyc2018;

https://leetcode-cn.com/problems/valid-perfect-square/solution/you-xiao-de-wan-quan-ping-fang-shu-by-leetcode/