Codeforces Round #257 (Div. 1)449A - Jzzhu and Chocolate(贪婪、数学)
主题链接:http://codeforces.com/problemset/problem/449/A
----------------------------------------------------------------------------------------------------------------------------------------------------------
欢迎光临天资小屋:http://user.qzone.qq.com/593830943/main
----------------------------------------------------------------------------------------------------------------------------------------------------------
Jzzhu has a big rectangular chocolate bar that consists of n × m unit squares. He wants to cut this bar exactly k times. Each cut must meet the following requirements:
- each cut should be straight (horizontal or vertical);
- each cut should go along edges of unit squares (it is prohibited to divide any unit chocolate square with cut);
- each cut should go inside the whole chocolate bar, and all cuts must be distinct.
The picture below shows a possible way to cut a 5 × 6 chocolate for 5 times.
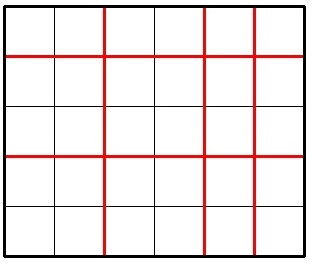
Imagine Jzzhu have made k cuts and the big chocolate is splitted into several pieces. Consider the smallest (by area) piece of the chocolate, Jzzhu wants this piece to be as large as possible. What is the maximum possible area of smallest piece he can get with exactlyk cuts? The area of a chocolate piece is the number of unit squares in it.
A single line contains three integers n, m, k (1 ≤ n, m ≤ 109; 1 ≤ k ≤ 2·109).
Output a single integer representing the answer. If it is impossible to cut the big chocolate k times, print -1.
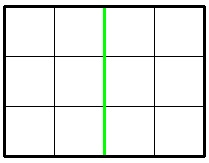
3 4 1
6
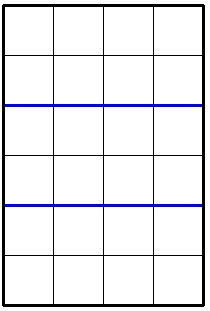
6 4 2
8
2 3 4
-1
In the first sample, Jzzhu can cut the chocolate following the picture below:
In the second sample the optimal division looks like this:
In the third sample, it's impossible to cut a 2 × 3 chocolate 4 times.
题意:给出一个 n * m 大小的chocolate bar。你须要在这个bar上切 k 刀,使得最小的部分面积尽可能大,求出这个被划分后的最小部分面积最大能够为多少。假设这个chocolate bar 不能切成 k 部分,则输出-1。
注意,每一刀须要符合3个条件:1、打横切或打竖切; 2、每一刀仅仅能经过unit square(即1*1的单元bar)的边,也就是说不能把一个单元bar损坏,要完整; 3、每一刀仅仅能在整个chocolate bar的里面操作,也就是说,外围的四条边是不同意切的。4、每一刀都是不同样的。
思路转载:
首先要知道什么时候这个大bar不能切成 k 刀。
非常easy知道是假设k > (n-1)+(m-1) 的情况,由于外围的四条边是不同意操刀的!排除这个不能切的情况后。那么就要依据是从n(打横切)还是从m(打竖切)来进行讨论了。
只是由于我们不能一眼看出哪种方案更优。所以两者都要讨论下,我一開始仅仅想到 if 中的两条式子,n/(k+1)的意思表示这 k 刀都打横切,而分母为什么是k+1而不是k。是由于一刀能够把一个区域分成两部分,两刀就三个部分,依次类推。而我们须要求的是面积,就须要用到部分,而不是刀数了。m/(k+1)依此类推。
只是问题出现了。我依据test10返回的wa结果来想出的^_^。
有可能全然打横切或者打竖切都没有切够k刀!那么就须要把剩余的刀数分到打竖切(相应之前全然打横切)或者打横切(相应之前的全然打竖切)中了。
也就是代码中else的部分。事实上完整的a1表达式是这种:n/(n-1) * m/(k-(n-1)+1)。意思:全然打横切,仅仅能切n-1刀,那么它划分的最小部分的面积就充当1了,至于m/(k-(n-1)+1) 表示 打竖切还能切多少刀,+1是由于是求分成的部分,而不是多少刀,与if中的n/(k+1)中的+1意思是同样的。
(好开心这道题目排到最少用时的26名。继续努力!
^_^)
代码例如以下:
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL __int64
int main()
{
LL n, m, k;
LL ans1, ans2;
while(~scanf("%I64d%I64d%I64d",&n,&m,&k))
{
if(n-1+m-1 < k)
{
printf("-1\n");
continue;
}
if(n >= k+1 || m >= k+1)
{
ans1 = n/(k+1)*m;
ans2 = m/(k+1)*n;
}
else
{
ans1 = n/(k-(m-1)+1)*1;
ans2 = m/(k-(n-1)+1)*1;
}
LL ans = max(ans1, ans2);
printf("%I64d\n",ans);
}
return 0;
}版权声明:本文博客原创文章,博客,未经同意,不得转载。


