42. 接雨水（Trapping Rain Water）

题目描述：

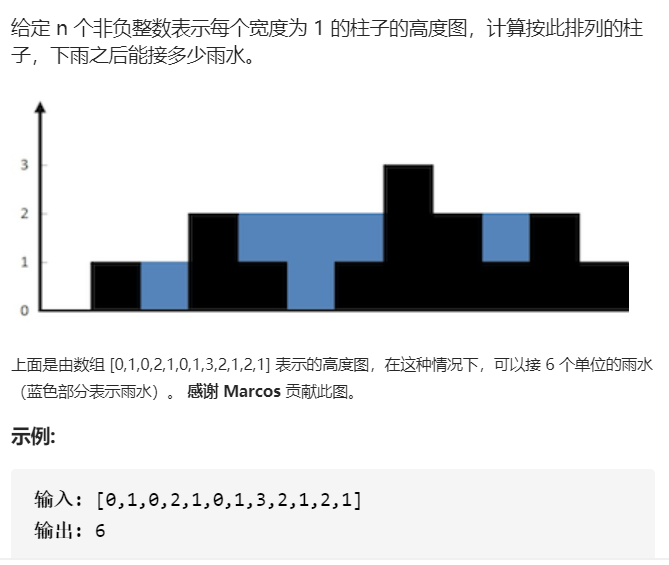
解题思路：

　　这道题主要是区分不同情况。假设从最左边的的柱子开始判断，因为该柱子的左边没有柱子，所以它一定是左边界柱子。那么我们就往右边寻找和这个柱子匹配的右边界柱子。有两种情况：

　　第一种情况，当右边有比该柱子高或一样高的柱子时，那么右边界柱子就一定是这根柱子，而中间的所有短柱子都是障碍物，所以我们需要计算左右边界的容量减去中间所有短柱子高度的和，就得到了这块区域最后的容量。之后以右边界柱子为起点，寻找下一个右边界柱子即可。

　　第二钟情况，当右边没有高度大于等于该柱子的柱子时，右边界柱子就是所有短柱子中最高的那一个。所以我们需要在遍历的过程中，记录下最高的短柱子的坐标。这种情况下，同样计算左右边界的容量减去中间柱子的高度和，就得到了最后的容量。然后以右边界柱子为起点，寻找下一个右边界柱子。

　　需要注意的是，我们可以在遍历过程中就记录中间短柱子的高度和，最后直接减去即可，避免重复遍历。另外左右两端如果有高度为0的柱子可以提前处理掉。

　　代码如下：

class Solution
{
public:
    int trap(vector<int>& height)
    {
        if (height.empty())
            return 0;
        auto p = height.end() - 1;
        while (p >= height.begin() && *p == 0)
            --p;
        if (p + 1 == height.begin())
            return 0;
        height.erase(p + 1, height.end());
        int ret = 0;
        int i = 0;
        while (i < height.size() && height[i] == 0)
            ++i;
        while (i < height.size() - 1)
        {
            int j = i + 1, tall = j, sum = 0, tall_sum = 0;
            while (j < height.size())
            {
                if (height[j] >= height[i])
                    break;
                if (height[tall] < height[j])
                {
                    tall = j;
                    tall_sum = sum;
                }
                sum += height[j];
                ++j;
            }

            if (j == height.size())
            {
                ret += (tall - i - 1) * height[tall] - tall_sum;
                i = tall;
            }
            else
            {
                ret += (j - i - 1) * height[i] - sum;
                i = j;
            }
        }
        return ret;
    }
};