深度学习 – 微积分、信息论 - 基本概念

 

 

微积分

 

• 导数：当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'(x0)或df(x0)/dx。其图像表示为如下：

     

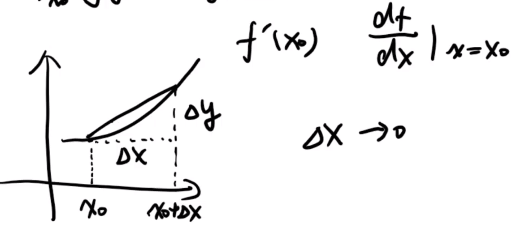
       类似的概念还有：二维空间中的“切线”。

 

 

 

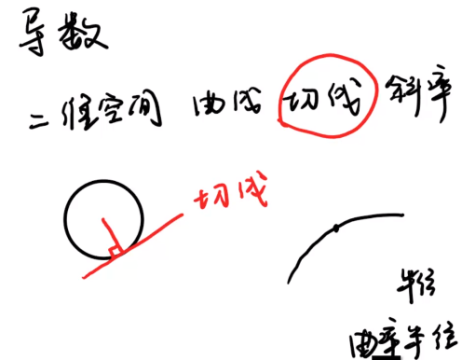
• 偏导数：当需要让其他变量不变，只有某一个变量发生变化，这种情况下的求导，其实际上表示的是函数在不同方向（坐标轴）上的变化率。
• 梯度：函数的所有偏导数构成的向量。梯度是一个向量，其向量的方向即为函数值增长最快的方向。

 

 

信息论

 

• 熵：也称信息熵，熵越大，不确定性越大。更多关于熵的解释请参看另一篇博客《机器学习 - 相关概念与实现流程》
• KL 散度：也称为相对熵，它衡量了两个分布之间的差异。若结合如下事实：

  • 真实事件的信息熵就是 p(xi) log p(xi)；

  • 理论拟合的事件的信息量就是 log q(xi)；

  • 真实事件的概率就是 p(xi)。

在模型优化、数据分析和统计等场合，就可以使用 KL 散度衡量选择的近似分布与数据原分布有多大差异 -- 当拟合事件和真实事件一致的时候 KL 散度就成了 0，不一样的时候就大于 0。

• 交叉熵：它也衡量了两个分布之间的差异，但是与 KL 散度的区别在于，交叉熵代表用拟合分布来表示实际分布的困难程度。

• 三者（熵、KL散度、交叉熵）的关系如下：

 

 

• 信息论的具体运用包括：函数中的交叉熵损失、机器学习中构建决策树使用到的信息增益、NLP 和语音算法中的维特比算法等。