属于线性代数，在深度学习领域的主要概念

 

深度学习核心的数据结构是标量、向量、矩阵和张量。

“张量”专属于深度学习TensorFlow框架的名词，这篇先简单汇总线性代数范围内的三种结构及其运算规则：标量、向量、矩阵。以及深度学习领域常用的一个概念：范数

 

1. 标量

    只有数值大小，没有方向的量。

 

 

2. 向量及其运算 （常使用的Python扩展程序库NumPy来操作）

   具有大小和方向的量。表示分别用不同向量的坐标做运算后所得坐标组合。

   

 

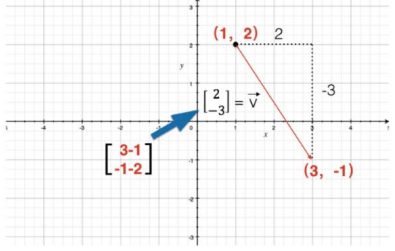
2.1 向量和标量的计算：直角坐标系中向量的数乘，就是向量坐标的分量分别乘该数。

 

 

2.2 向量之间的加减操作：直角坐标系中向量的加减就是对应坐标分量的加减。如下展示：加法运算

 

 

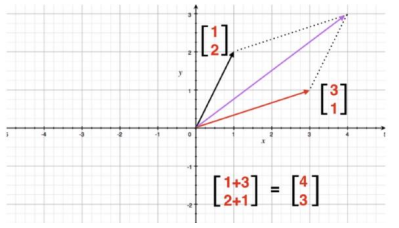
2.3 向量之间的乘法操作：主要分为点乘（内积）、叉乘（外积）和对应项相乘。

 

• • 向量的点乘，也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。向量的点乘要求两个向量的长度一致。
  • 向量的叉乘，也叫向量的外积、向量积。叉乘的运算结果是一个向量而不是一个标量。叉乘用得较少。
  • 对应项相乘，就是两个向量对应的位置相乘，得到的结果还是原来的形状。

 

 

3. 矩阵及其运算

    按照长方阵列排列的复数或实数集合。

 

3.1 矩阵的加减法：相同"形状"的矩阵对应元素做加减法，同型矩阵才可以做加减法。

        

 

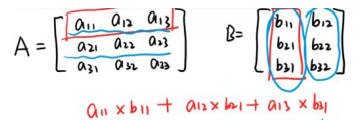
3.2 矩阵的乘运算：结果矩阵的第 i 行第 j 列元素为第一个矩阵的第 i 行元素分别乘第二 个矩阵的第 j 列元素再做加和。

         

• • 乘运算也有两种形式：第一种是两个形状一样的矩阵的对应位置分别相乘。第二种则是矩阵乘法。
  • 第一个矩阵的列数等于第二个矩阵的行数，两个矩阵才可以相乘。
  • 矩阵的乘法不满足交换律。

 

4. 范数

    范数是一种距离的表示，或者说向量的长度。常见的范数有 L0 范数、L1 范数和 L2 范数。

 

4.1 L0 范数

              L0 范数指这个向量中非 0 元素的个数。我们可以通过 L0 范数减少非 0 元素的个数，从而减少参与决策的特征，减少参数。

 

4.2 L1 范数

              L1 范数指的是向量中所有元素的绝对值之和，它是一种距离的表示（曼哈顿距离），也被称为稀疏规则算子。

 

4.3 L2 范数

              L2 范数是向量中所有元素的平方和的平方根，很常用的一类范数，其实也代表一种距离，即欧式距离。

 

各类范数的作用：

• • L0和L1范数的作用：权值稀疏

在设计模型的过程中，我们有时会使用到大量的特征，每个特征都会从不同的角度体现问题的不同信息。这些特征经过某些方式的组合、变换、映射之后，会按照不同的权重得到最终的结果。但有时候，有一部分特征对于最后结果的贡献非常小，甚至近乎零。这些用处不大的特征，我们希望能够将其舍弃，以更方便模型做出决策。这就是权值稀疏的意义。

 

L0 范数和 L1 范数都能实现权值稀疏。但 L1 范数是 L0 范数的最优凸近似，它比 L0 范数有着更好的优化求解的特性，所以被更广泛地使用。

 

 

• • L2范数的作用是：防止过拟合

如果我们要避免模型过拟合，就要使 L2 最小，这意味着向量中的每一个元素的平方都要尽量小，且接近于 0。

L1 会趋向于产生少量的特征，而其他的特征都是 0，用于特征选择和稀疏；L2 会选择更多的特征，但这些特征都会接近于 0，用于减少过拟合。