LeetCode 最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba"也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
方法一 动态规划:
对于字符串str,假设dp[i,j]=1表示str[i...j]是回文子串,那个必定存在dp[i+1,j-1]=1。这样最长回文子串就能分解成一系列子问题,可以利用动态规划求解了。首先构造状态转移方程
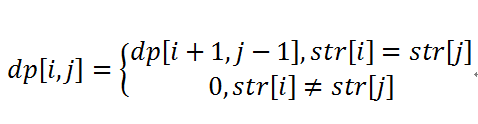
上面的状态转移方程表示,当str[i]=str[j]时,如果str[i+1...j-1]是回文串,则str[i...j]也是回文串;如果str[i+1...j-1]不是回文串,则str[i...j]不是回文串。
初始状态
- dp[i][i]=1
- dp[i][i+1]=1 if str[i]==str[i+1]
上式的意义是单个字符,两个相同字符都是回文串。
我们只需要数组的右上部分,首先将数组初始化为全0数组 arr = [[0 for col in range(l)] for row in range(l)]
注意计算顺序为斜向计算
例如:绿色为初始化顺序,红色为计算顺序

1 class Solution(object): 2 def longestPalindrome(self, s): 3 """ 4 :type s: str 5 :rtype: str 6 """ 7 l = len(s) 8 start = 0 9 longest = 1 10 arr = [[0 for col in range(l)] for row in range(l)] # 数组初始化 11 # l * l arr[i][j]表示i-j是否为回文串, 数组只使用右上部分 12 # 首先,所有的单个字符均为回文串 13 for i in range(l): 14 arr[i][i] = 1 15 # 其次,两个字符的 16 for i in range(l-1): 17 if s[i] == s[i+1]: 18 arr[i][i+1] = 1 19 start, longest = i, 2 20 21 for i in range(3, l+1):# 回文串的长度 22 for j in range(l-i+1): 23 # [j][j+l-1] 24 if s[j] == s[j+i-1] and arr[j+1][j+i-2] == 1: 25 arr[j][j+i-1] = 1 26 start, longest = j, i 27 28 29 return s[start:start+longest]





