（原创）最小生成树之Prim（普里姆）算法+代码详解，最懂你的讲解

Prim算法

（哈欠）在创建最小生成树之前，让我们回忆一下什么是最小生成树。最小生成树即在一个待权值的图（即网结构）中用一个七拐八绕的折线串连起所有的点，最小嘛，顾名思义，要权值相加起来最小，你当然可以拿起笔来就算你脑中的每一种可能，但是如果你了解了这种算法，你就能跟我一样，一次画出完美答案。

上个栗子：

我先说一哈这个算法的方法论，然后我们来代码实现一下，在讲解开始之前，敲黑板，记得我们要生成一个权值最小的树，所以每一步都要考虑到树的每一个结点，不要孤立地用一个结点来对比从而走上死路，我们任选一个点开始生成，教材里选的 v0，那我们就选 v8，战斗开始

v8 有三条路，分别通往v1 v2 v3，v2那条路权值最小，ok， v2→v8，然后我们该看什么，如果你说找和 v2 相邻的 v8 以外的边，那我刚才的强调就gg了，我们找v2 和 v8除相连的线之外的所有分支，易得 v8→v1的权值最小，ok，下一步找哪几个点？v2 v1 v8这三个点除两条连接线以外的所有分支，挑最小的那一条，后面重复前面的操作，每次都把新加入的伙伴算在找线之内才对，自己画一下给答案：

 

 

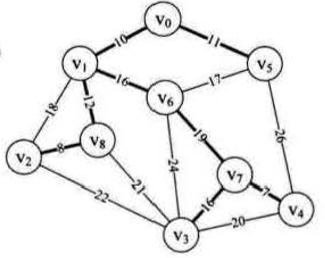
操作一遍是不是发现还真的跟哪个点开始没鸡儿关系，因为每个点都要连到，关键就在于沿最小分支找点的时候一定要把它看成一个树结构来找，才算是最小生成树。

还是给一下标准定义：

我们把构造连通网的最小代价（权值）生成树 称为最小生成树 （Minimum Cost Spanning Tree）。

方法论就到这里，相信下一次看到同样的现实问题，你也应该能在第一时间用正确的思路找到合适的路。

在代码实现之前，我们先请来连通图的好基友——邻接矩阵

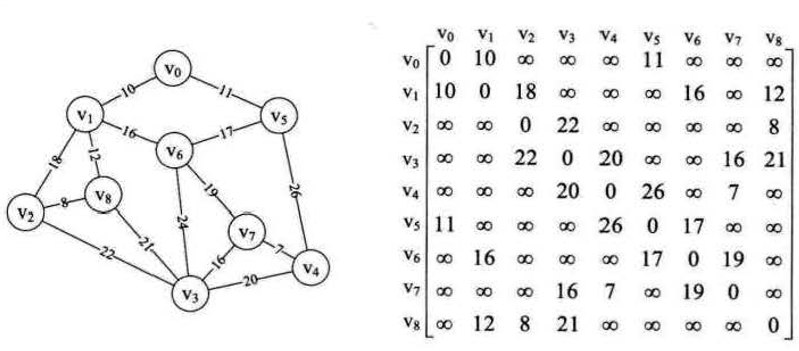
我们发现一行一行的矩阵很容易显示权值，这样就可以快速对比权值的大小，只要在循环的每一步留存下权值较小的边权值和顶点下标，就可以实现。

和以前一样，我们还是用 INFINITY 来表示无限大，即不存在该边

代码如下：

void MiniSpanTree_Prim(MGragh G)
{
    int mini,i,j,k;
    int adjvex[MAXVEX]; //保存相关顶点下标
    int lowcost[MAXVEX]; //保存相关顶点间边的权值
    lowcost[0] = 0;//这里把第0位的权值置0表示v0已加入生成树
    //ps：lowcost[i] = 0 表示i那个下标的顶点加入生成树
    adjvex[0] = 0; //初始化第一个顶点的下标为0
    for(i = 0; i < G.numVertexes; i++)
    {
        lowcost[i] = G.arc[0][i];//将vo相关顶点的权值存入lowcost数组
        adjvex[i] = 0;//置所有下标为v0
    }
    for(i = 1; i < G.numVertexes; i++) //最小生成树开始辽
    {
        mini = INFITINY; //先把权值的最小值置为无限大
        j = 1;
        k = 0;
        while(j < G.numVertexes)
        {
            if(lowcost[j] != 0 && lowcost[j] < mini)//判断并向lowcost中添加权值
            {
                mini = lowcost[j];
                k = j;
            }
            j++;
        }
        printf("(%d %d)",lowcost[k],k);
        lowcost[k] = 0;//置0表示这个定点已经完成任务，找到最小权值分支
        for(j = 1; j < G.numVertexes; j++)
        {
            if(lowcost[j] != 0 && G.arc[k][j] < lowcost[j])
            {
                lowcost[j] = G.arc[k][j];
                adjvex[j] = k;
            }
        }
    }
}

简单讲解一哈：

• 4~5行，先说 adjvex[] ，这个数组要解决的问题就是存入已经安排好的那些顶点的下标，什么叫安排好了呢，比如我已经找到了 v0→v1 ，v1 就可以算是安排好了，而v0点置0则算做初始化的操作；再说 lowcost[] 这个数组，听名字就是最小权值的意思，下面讲循环的时候详解这个东西到底储存了些什么，然后每次更新之后能做什么
• 6~13行完全是初始化，要注意的是就是 lowcost[] 储存了邻接矩阵 v0 这一行的权值
• 14~38行是最小生成树的整体代码
• 16行就是每次都把最小值重置
• 19~27行，从 1 开始遍历完全，找到现在这个状态下的最小权值数，并且把这个下标用 k 存住，28行就是把权值和下标打印出来，当然也可以换成别的操作，这里不再赘述
•  然后29行，看看他都干了些什么，它把  adjvex[ k ] 置0，看一下第一点，这里表示 v1 完成任务，没有利用价值了
• 然后30~37这个循环，看看循环的条件，条件一：   lowcost[ j ] != 0  ，这是啥意思，表示在没有完成任务的顶点中选择，条件二：  G.arc[k][j] < lowcost[j]   这表示在刚才找到的新顶点的矩阵那一行去对应，如果有更小的权值就把 lowcost[] 更新掉，这样就保证了这个数组中同时存在好几个顶点的权值信息，还是择优录用的，然后返回循环头，再找这次的最小权值点，周而复始。

时间复杂度 O（n²） ，没啥问题辽

最后附上过程图：

 

谢谢大嘎