写在开头：B-树，就是B树。因B树的英文名称为B-tree ，B-树因此而来，有人会误以为B-树是一种树，而B树又是另外一种树。实际上，B-tree就是指的B树。
而且B-树不可以读成B减树。。。
一：预备知识：
磁盘I/O：是指磁盘的输入和输出(Input和Output的缩写)。
二叉查找树（Binary Sort Tree），简称BST，其查找的时间复杂度O(log2N)与树的深度相关，那么降低树的深度自然会提高查找效率。数据库索引一般使用B树存储，其索引存在磁盘中，利用索引查询时，对于数据量大的索引不可能一次全部加载，只是一次次加载磁盘页，在B树中，每个节点的大小为一个磁盘的页。在大量数据中实现索引查询时 ，树节点存储的元素数量是十分有限的，如果元素数量非常多的话，查找就退化成节点内部的线性查找了，二叉查找树结构会因树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下，磁盘查找存取的次数往往由树的高度所决定，为了减少树的深度 我们采用多叉树结构
我们通过 减少树的结构尽量减少树的高度， 减少磁盘查找存取的次数 我们就想到了多路查找树。 许多数据库系统都一般使用B树或者B树的各种变形结构。一棵含n个结点的B树的高度为O（lgn）。
B 树又叫平衡多路查找树。它的每一个节点最多包含k个孩子，k便称为B树的阶。k的大小取决于磁盘页的大小。
1.树中每个结点含有最多含有k个孩子，即k满足：ceil(k/2)<=k<=k （ceil(x)是一个取上限的函数）；
2.除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子
3..根节点至少有两个孩子
4..所有叶子结点都出现在同一层
5..每个节点中元素从小到大排列
6..中间的节点有k-1个元素和k个孩子
当单一节点元素很多时，B树在查询时次数不比二叉查找树小，
二：插入：
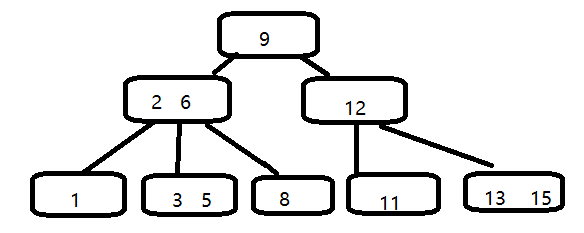
若要插入4，，自顶向下查找4的节点位置，4应该插在3，5之间，2，6和3，5都是两元素节点，无法增加根节点可以升级为两元素结点，4，9.
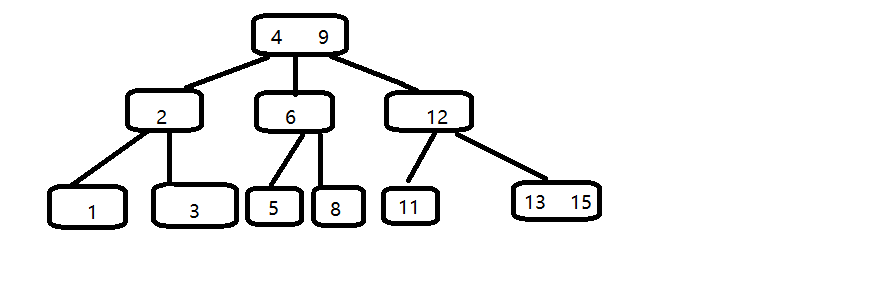
以下节点为符合规则也要改变，维持多路平衡。
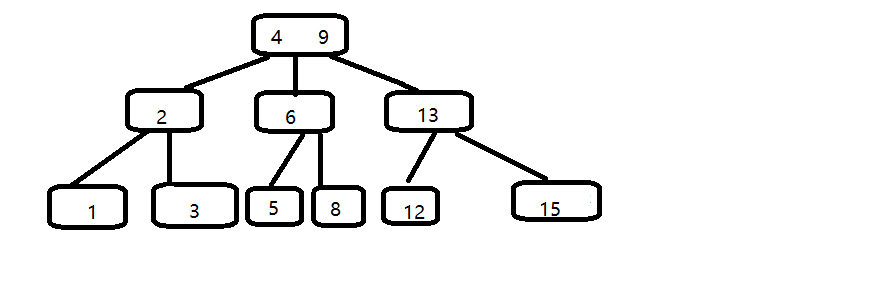
三：删除
例如，我们要删除11，但是12不可只有一个孩子，我们找出12，13，15中的中位数13作为父节点，12下移成为左孩子。
四：应用：
用于部分数据库索引，文件系统等
