【ARC101F】Robots and Exits 树状数组
题目大意
有 \(n\) 个机器人和 \(m\) 个出口。
这 \(n\) 个机器人的初始位置是 \(a_1,a_2,\ldots,a_n\),这 \(m\) 个出口的位置是 \(b_1,b_2,\ldots,b_m\)。
你每次可以让所有机器人往左走一步或往右走一步。
当一个机器人所在的位置有一个出口时,这个机器人就会从这个出口出去。
问你有多少种让机器人全部离开的方案。
两种方案不同当且仅当有至少一个机器人从不同的出口出去。
\(n,m\leq 100000\)
题解
先把最左边的出口左边的机器人和最右边的出口右边的机器人还有已经在出口的机器人全部删掉。
对于一个机器人,设它到左边出口的距离为 \(a_i\),到右边出口的距离为 \(b_i\)。可以把它看成一个点 \((a_i,b_i)\)。
记 \(x\) 是所有机器人往左移动的最远点到初始位置的距离,\(y\) 是所有机器人往右移动的最远点到初始位置的距离。
那么每次可以选择把 \((x,y)\) 变成 \((x+1,y)\) 或者 \((x,y+1)\)。
当 \(x=a_i\) 时,第 \(i\) 个机器人会从左边的出口出去,当 \(y=b_i\) 时,机器人会从右边的出口出去。
那么可以看成从原点开始走,每次往上或右走一步。最后走的这条折线的上方和下方分别对应着从左边和右边的出口出去的机器人的集合。
那么考虑把折线往下移,变成这样:
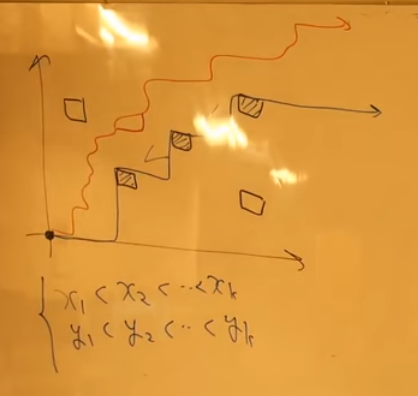
那么一条折线可以用折线经过的点(那些涂黑的格子)来表示。
设 \(f_i\) 为最后一个经过的黑色格子是 \(i\) 的方案数。
\(f_i=1+\sum_{x_j<x_i,y_j<y_i}f_j\)
用树状数组维护。
时间复杂度: \(O(n\log n)\)
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<ctime>
#include<utility>
#include<functional>
#include<cmath>
#include<vector>
//using namespace std;
using std::min;
using std::max;
using std::swap;
using std::sort;
using std::reverse;
using std::random_shuffle;
using std::lower_bound;
using std::upper_bound;
using std::unique;
using std::vector;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef std::pair<int,int> pii;
typedef std::pair<ll,ll> pll;
void open(const char *s){
#ifndef ONLINE_JUDGE
char str[100];sprintf(str,"%s.in",s);freopen(str,"r",stdin);sprintf(str,"%s.out",s);freopen(str,"w",stdout);
#endif
}
int rd(){int s=0,c,b=0;while(((c=getchar())<'0'||c>'9')&&c!='-');if(c=='-'){c=getchar();b=1;}do{s=s*10+c-'0';}while((c=getchar())>='0'&&c<='9');return b?-s:s;}
void put(int x){if(!x){putchar('0');return;}static int c[20];int t=0;while(x){c[++t]=x%10;x/=10;}while(t)putchar(c[t--]+'0');}
int upmin(int &a,int b){if(b<a){a=b;return 1;}return 0;}
int upmax(int &a,int b){if(b>a){a=b;return 1;}return 0;}
const ll p=1000000007;
const int N=100010;
int cmp(pii a,pii b)
{
if(a.first!=b.first)
return a.first<b.first;
return a.second>b.second;
}
int n,m,t,t2;
int a[N],b[N],d[N];
pii c[N];
ll e[N];
ll add(ll a,ll b)
{
a+=b;
return a>=p?a-p:a;
}
void add(int x,ll v)
{
for(;x<=t2;x+=x&-x)
e[x]=add(e[x],v);
}
ll sum(int x)
{
ll s=0;
for(;x;x-=x&-x)
s=add(s,e[x]);
return s;
}
int main()
{
open("arc101f");
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=m;i++)
scanf("%d",&b[i]);
for(int i=1;i<=n;i++)
if(a[i]>b[1]&&a[i]<b[m])
{
int x=lower_bound(b+1,b+m+1,a[i])-b;
if(b[x]==a[i])
continue;
c[++t]=pii(a[i]-b[x-1],b[x]-a[i]);
d[++t2]=b[x]-a[i];
}
sort(d+1,d+t2+1);
t2=unique(d+1,d+t2+1)-d-1;
for(int i=1;i<=t;i++)
c[i].second=lower_bound(d+1,d+t2+1,c[i].second)-d;
sort(c+1,c+t+1,cmp);
t=unique(c+1,c+t+1)-c-1;
ll ans=1;
for(int i=1;i<=t;i++)
{
ll s=sum(c[i].second-1)+1;
ans+=s;
add(c[i].second,s);
}
ans%=p;
printf("%lld\n",ans);
return 0;
}







