【XSY2753】Lcm 分治 FWT FFT 容斥
题目描述
给你\(n,k\),要你选一些互不相同的正整数,满足这些数的\(lcm\)为\(n\),且这些数的和为\(k\)的倍数。
求选择的方案数。对\(232792561\)取模。
\(n\leq {10}^{18},k\leq 20\),\(n\)的全部质因子都\(\leq 100\)
题解
解法一
一个\(\leq {10}^{18}\)的数最多有\(15\)不同的质因子。
记\(w=15,m=2^w=32768\)
先看看这个模数有什么特点。
\(p=232792561=lcm(1,2,\ldots,20)+1\)
这告诉我们可以对长度在\(1\ldots 20\)的区间DFT。
所以可以在所有用到模\(k\)的余数的地方DFT,然后对于每个余数做要做的事情。
对于一个数,如果这个数的某个质因子的最高次幂\(\neq n\)的这个质因子的最高次幂,这个质因子是没有用的。
这样可以把一个数\(x\)表示成一个数对\(g(x)=(i,j)\),其中\(i\)是一个状态,表示\(x\)有哪些质因子的最高次幂和\(n\)的最高次幂相同。\(j\)表示这个数模\(k\)的余数。
先暴力枚举所有\(n\)的因子(\(\approx {10}^5\)个),记\(a_{i,j}\)表示有多少个数\(x\)对应的数对\(g(x)=(i,j)\)。
现在对于每一个\(i\),计算只取这些数,和模\(k\)为\(j=0\ldots k-1\)的方案数\(f_{i,j}\)。
记\(F_i(x)=\sum_{i=0}^{k-1}f_{i,j}x^j\),那么有\(F_i(x)=\prod_{i=0}^{k-1}{(1+x^i)}^{a_{i,j}}\mod x^k\)。(当然你也可以用一些其他的方法计算,比如说每加一个数进去就维护一下)
算出\(F_i(x)\)之后做一遍DFT,这样各个\(j\)之间就互不影响了。在做完接下来的步骤后IDFT回来,然后取\(j=0\)的值就是答案了。
剩下的步骤我们认为\(k=1\),即不考虑模\(k\)的余数。
现在我们要取一些\(i\)出来,满足\(i_1~or~i_2~or,\cdots,or~i_m\),把答案加上\(f_{i_1}f_{i_2}\cdots f_{i_m}\)。
令\(g_{i,j}=\begin{cases}f_i&j=i\\0&j\neq i\end{cases}\),那么我们要求的答案就是一个类似\(g_1\oplus g_2\oplus\cdots\oplus g_m\)的东西(实际上在DFT之前\(g_{i,0}\)要\(+1\)表示不选,DFT之后每一位都要\(+1\))。这里\(\oplus\)是集合或卷积。
直接做的复杂度是\(O(w4^w)\),太慢了。
注意到\(g_i\)只有一项非零,所以可能有更快的做法。
考虑分治,观察怎么把两个状态合并。
合并的时候记左边的结果为
\(A_1\),右边的结果为\(A_2\),那么合并之后的就是\(A_1+A_2+A_1A_2\)。
合并的两个数组是长这样的:
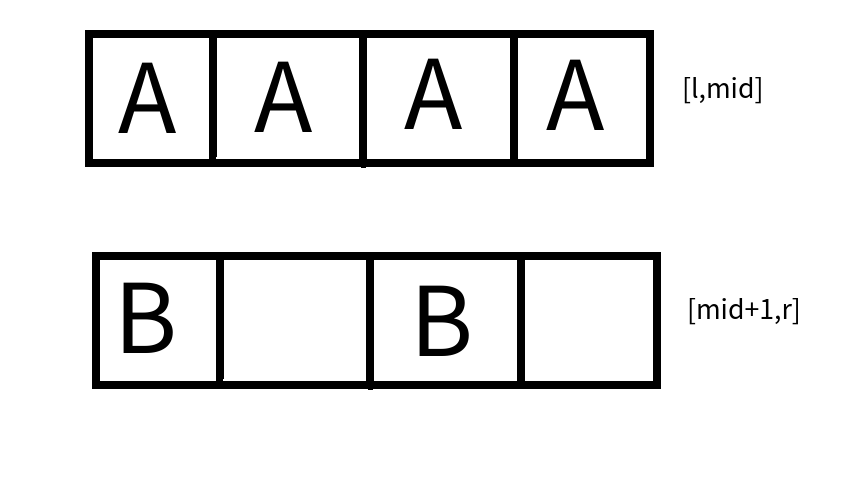
整个数组是一个部分重复很多次。

我们可以只储存&计算循环节部分,要用更长的部分的时候再扩展。
另一种理解是:每个\(g_{i,j}\)对答案的\(s_l(j\subseteq l)\)都有贡献,这个贡献是乘上去的(因为是在FWT后对应位乘起来)。
因为前面已经做过一次求幂了(\(F_i(x)\)),所以你也可以这几步先不做(求幂和乘法),在最后做一次求幂。这个就是下面的容斥做法。
总时间复杂度是\(O(k^22^w+kw2^w)\)
解法二
一个容斥的做法。
记\(g_{i,j}\)为有多少个数满足:对于\(i\)中每个\(1\)的二进制位,这些位对应的质因子的次数要取到上限,剩下位的可以任意取,且这个数模\(k\)为\(j\)。
\(G_i(x)=\sum_{j=0}^{k-1}{(1+x^j)}^{g_{i,j}}\)
然后容斥一下,容斥过程就是IFWT。
那么把这个东西做一遍IFWT就是答案了。
时间复杂度和上面的差不多。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int p=232792561;
const int root=71;
ll fp(ll a,ll b)
{
ll s=1;
for(;b;b>>=1,a=a*a%p)
if(b&1)
s=s*a%p;
return s;
}
int w[1010];
int w2[1010];
ll n;
int m,k,cnt;
ll a[200010];
int d[100];
int c[100];
ll e[100];
int all;
void dft(int *a,int n)
{
static int b[100];
for(int i=0;i<n;i++)
b[i]=0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
b[i]=(b[i]+(ll)a[j]*w[i*j])%p;
for(int i=0;i<n;i++)
a[i]=b[i];
}
void idft(int *a,int n)
{
static int b[100];
for(int i=0;i<n;i++)
b[i]=0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
b[i]=(b[i]+(ll)a[j]*w2[i*j])%p;
int inv=fp(n,p-2);
for(int i=0;i<n;i++)
a[i]=(ll)b[i]*inv%p;
}
void getfactor(int x,ll s)
{
if(x>m)
{
a[++cnt]=s;
return;
}
for(int i=0;i<=d[x];i++,s*=c[x])
getfactor(x+1,s);
}
int f[50000][20];
int g[50000][20];
void gao(int x,int y,int s)
{
if(x==0)
{
// for(int i=0;i<k;i++)
// f[y][i]=b[s][i];
// dft(f[y],k);
// idft(f[y],k);
return;
}
gao(x-1,y,s);
gao(x-1,y+(1<<(x-1)),s|(1<<(x-1)));
for(int i=y+(1<<(x-1));i<y+(1<<x);i++)
for(int j=0;j<k;j++)
{
g[i][j]=f[i][j];
f[i][j]=f[i-(1<<(x-1))][j];
// f[i][j]=1;
}
for(int i=y;i<y+(1<<(x-1));i++)
for(int j=0;j<k;j++)
// g[i][j]=1;
g[i][j]=0;
for(int i=y;i<y+(1<<x);i++)
for(int j=0;j<k;j++)
f[i][j]=(f[i][j]+g[i][j]+(ll)f[i][j]*g[i][j])%p;
}
void add(int x,int y)
{
static int c[20];
for(int i=0;i<k;i++)
c[i]=f[x][i];
for(int i=0;i<k;i++)
f[x][(i+y)%k]=(f[x][(i+y)%k]+c[i])%p;
f[x][y]=(f[x][y]+1)%p;
}
void solve()
{
scanf("%lld%d",&n,&k);
w[0]=1;
ll rt=fp(root,(p-1)/k);
for(int i=1;i<=1000;i++)
w[i]=(ll)w[i-1]*rt%p;
for(int i=0;i<=1000;i++)
w2[i]=fp(w[i],p-2);
m=0;
for(int i=2;i<=100;i++)
if(n%i==0)
{
m++;
c[m]=i;
d[m]=0;
e[m]=1;
while(n%i==0)
{
n/=i;
d[m]++;
e[m]*=i;
}
}
cnt=0;
getfactor(1,1);
memset(f,0,sizeof f);
for(int i=1;i<=cnt;i++)
{
int s=0;
for(int j=1;j<=m;j++)
if(a[i]%e[j]==0)
s|=1<<(j-1);
add(s,a[i]%k);
}
for(int i=0;i<1<<m;i++)
{
f[i][0]++;
dft(f[i],k);
}
// gao(m,0,0);
for(int i=1;i<1<<m;i<<=1)
for(int j=0;j<1<<m;j++)
if(j&i)
for(int l=0;l<k;l++)
f[j][l]=(ll)f[j][l]*f[j-i][l]%p;
// for(int j=1;j<1<<m;j<<=1)
// for(int l=0;l<1<<m;l++)
// if(j&l)
// for(int i=0;i<k;i++)
// f[l][i]=(f[l][i]-f[l-j][i])%p;
int all=(1<<m)-1;
for(int i=0;i<all;i++)
{
int v=1;
for(int j=0;j<m;j++)
if(!((i>>j)&1))
v=-v;
for(int j=0;j<k;j++)
f[all][j]=(f[all][j]+v*f[i][j])%p;
}
idft(f[all],k);
ll ans=f[all][0];
ans=(ans+p)%p;
printf("%lld\n",ans);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
#endif
int t;
scanf("%d",&t);
while(t--)
solve();
return 0;
}







