【XSY2774】学习 带花树
题目描述
给你一个图,求最大匹配。
边的描述方式很特殊,就是一次告诉你\(c_i\)个点:\(d_1,d_2,\ldots,d_{c_i}\),表示这些点两两之间都有连边,也就是说,这是一个团。总共有\(m\)个团。
记\(s=\sum_{i=1}^mc_i\)。
\(n,m,s\leq 3000\)
题解
直接跑带花树的话时间复杂度是\(O(ns^2\alpha(n))\)的,显然会TLE。
假设每个\(c_i\)都是偶数(如果是奇数就让最后一个点像前面的点连边,然后把这个点去掉)。
对于每一个团,添加\(k=c_i\)个辅助点,按以下方式连边(红色的为原来的店,蓝色的为辅助点):
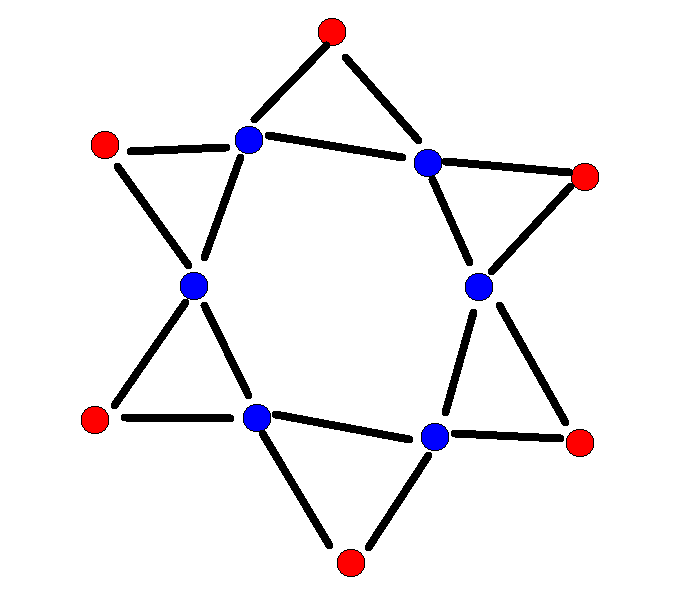
易证有\(x\)个红色点和蓝色点匹配时,最大匹配是\(\lfloor\frac{x+k}{2}\rfloor\)。
(可以先选一个红色点匹配,然后顺时针确定其他红色点,对这个红色点相邻的蓝色点到上一个红色点相邻的蓝色点之间蓝色点个数分类讨论来决定这个红色点连向那个蓝色点。)
对于每个团,令\(k\)为偶数,然后在跑完带花树后把答案减掉\(\sum k/2\)。
这样建图的边的个数是\(O(s)\)的。
时间复杂度:\(O(ns\alpha(n))\)
(显然\(O(n\alpha(n))\)的并查集常数很大会被卡常。)
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<utility>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
int rd()
{
int s=0,c;
while((c=getchar())<'0'||c>'9');
s=c-'0';
while((c=getchar())>='0'&&c<='9')
s=s*10+c-'0';
return s;
}
void open(const char *s)
{
#ifndef ONLINE_JUDGE
char str[100];
sprintf(str,"%s.in",s);
freopen(str,"r",stdin);
sprintf(str,"%s.out",s);
freopen(str,"w",stdout);
#endif
}
struct graph
{
int h[6010];
int v[10000010];
int t[10000010];
int n;
void clear()
{
memset(h,0,sizeof h);
n=0;
}
void add(int x,int y)
{
n++;
v[n]=y;
t[n]=h[x];
h[x]=n;
}
};
graph g;
int n,m;
int ans;
int c[6010];
int f[6010];
int find(int x)
{
return f[x]==x?x:f[x]=find(f[x]);
}
int link[6010];
int d[6010];
int b[6010];
int q[6010];
int pre[6010];
int head,tail;
void aug(int x)
{
for(int y=pre[x];x;x=pre[y],y=pre[x])
{
link[x]=y;
pre[y]=link[y];
link[y]=x;
}
}
int vis[6010];
int ti=0;
int getlca(int x,int y)
{
ti++;
for(x=find(x),y=find(y);;swap(x,y))
if(x)
{
if(vis[x]==ti)
return x;
vis[x]=ti;
x=find(pre[link[x]]);
}
return 0;
}
void gao(int x,int y,int lca)
{
for(;find(x)!=lca;x=pre[y])
{
pre[x]=y;
y=link[x];
f[x]=lca;
f[y]=lca;
if(d[y])
{
d[y]=0;
q[++tail]=y;
}
}
}
int num;
int bfs(int x)
{
memset(b,0,sizeof b);
for(int i=1;i<=num;i++)
f[i]=i;
head=1,tail=0;
d[x]=0;
b[x]=1;
q[++tail]=x;
int v;
while(tail>=head)
{
x=q[head++];
for(int i=g.h[x];i;i=g.t[i])
if(find(v=g.v[i])==find(x))
continue;
else
{
if(!b[v])
{
pre[v]=x;
b[v]=1;
if(!link[v])
{
aug(v);
return 1;
}
else
{
b[link[v]]=1;
d[v]=1;
d[link[v]]=0;
q[++tail]=link[v];
}
}
else
{
if(!d[v])
{
int lca=getlca(x,v);
gao(x,v,lca);
gao(v,x,lca);
}
}
}
}
return 0;
}
void solve()
{
num=n;
g.clear();
int x,y;
ans=0;
for(int i=1;i<=m;i++)
{
scanf("%d",&x);
for(int j=1;j<=x;j++)
scanf("%d",&c[j]);
sort(c+1,c+x+1);
x=unique(c+1,c+x+1)-c-1;
if(x&1)
{
for(int j=1;j<x;j++)
{
g.add(c[j],c[x]);
g.add(c[x],c[j]);
}
x--;
}
for(int j=1;j<=x;j++)
{
g.add(num+j,num+j%x+1);
g.add(num+j%x+1,num+j);
}
for(int j=1;j<=x;j++)
{
g.add(c[j],num+j);
g.add(num+j,c[j]);
g.add(c[j],num+j%x+1);
g.add(num+j%x+1,c[j]);
}
ans-=x/2;
num+=x;
}
memset(link,0,sizeof link);
for(int i=1;i<=num;i++)
if(!link[i])
{
if(bfs(i))
ans++;
}
printf("%d\n",ans);
}
int main()
{
open("c");
while(~scanf("%d%d",&n,&m)&&(n||m))
solve();
return 0;
}







