一些算法（套路）

目录

容易被忽略的东西

分块

二分答案

打表

差分

线段树优化DP

差分约束

　　如果只有 \(a_i\leq a_j+d\) 的约束，就可以直接上差分约束。

　　如果有 \(a_i+a_j\leq d\) 的约束，考虑整张图黑白染色，使得同色点之间只有差的约束，异色点之间只有和的约束，然后把白色的点的值取反，就可以跑差分约束了。

矩阵快速幂

　　观察一下矩阵是否是循环矩阵，如果是就可以用FFT解决（循环卷积）。

用BM算法优化矩阵快速幂DP

　　记 \(B\) 为转移矩阵。

　　那么 \(B\) 中每个元素都对应着同一个常系数线性递推关系。

　　证明：

　　记 \(B\) 的特征多项式为 \(f(x)=a_0x^k+a_1x^{k-1}+\cdots+a_kx^0\)，那么就有

\[\begin{align} (a_0B^k+a_1B^{k-1}+\cdots+a_kB^0)&=0\\ B^t(a_0B^k+a_1B^{k-1}+\cdots+a_kB^0)&=0\\ a_0B^{k+t}&=-a_1B^{k-1+t}-a_2B^{k-2+t}-\cdots-a_kB^t\\ \end{align} \]

　　这样就可以求出前面 \(O(k)\) 项然后 \(O(k^2)\) BM一下得到递推式再用倍增取模在 \(O(k^2\log n)\) 或 \(O(k\log k\log n)\) 内求出任意项的值了。

　　如果要求整个矩阵的递推式的话，要拿这个矩阵哈希得到的值去BM，因为单项的最短递推式可能不是整个矩阵的最短递推式。
　

矩阵快速幂+DFT

　　DP转移如下：

\[f_{i+1,j',k+v}+=f_{i,j,k} \]

　　\(i\leq n,j\leq l,k\leq m\)
　　其中\(v\)只与\(j\)有关，最后求\(k=s\)或\(k\bmod m=s\)的值的和。
　　暴力搞的时间复杂度是\(O(l^3m^3\log n)\)的。
　　我们可以把这个东西看成一个多项式。

\[g_{i,j}=\sum_{k\geq 0}f_{i,j,k}x^k \]

　　
　　转移就可以看成乘以一个多项式（单项式）。
　　如果求的是\(k\mod m=s\)的值的和，就可以看成循环卷积。
　　可以先求值，把每个点值拿去跑一遍矩阵快速幂，再插值回来。
　　时间复杂度：\(O(ml^3\log n)+\)点值插值的时间复杂度\(O(m^2)/O(m\log m)\)

多组询问的矩阵快速幂优化DP

　　设矩阵大小为\(m\)，次数是\(n\)，询问组数是\(t\)，朴素的实现是\(O(tm^3\log n)\)的。
　　可以先把转移矩阵的\(i\)次幂求出来。
　　每次询问只需要拿一个\(1\times m\)的矩阵去乘转移矩阵就行了。每次乘法是\(O(m^2)\)的。
　　时间复杂度：\(O(m^3\log n+tm^2\log n)\)

带删除的线性基

　　对于线性基中的每个向量和所有 \(0\) 向量维护这个向量是由哪些向量异或得到的。

　　在删除一个向量 \(x\) 时，找到一个包含 \(x\) 的 \(0\) 向量，如果没有就找线性基里位最低的包含 \(x\) 的向量，把这个向量的信息异或到其他包含 \(x\) 的向量的信息中即可。这样在删除时不会影响线性基中更高位的向量。

　　在向量个数比较小或强制在线是比较有用。

排序

　　有些题如果把权值（或者其他东西）从小到大排序按顺序做，会有出人意料的效果。

定期重构

　　就每做 \(O(\sqrt q)\) 个修改就重构一下，每次询问在建好的数据结构上查询，还要把剩下的 \(O(\sqrt q)\) 的修改的影响一起算进去。

概率/期望DP

　　有一些概率/期望DP可以快速地推出这样的式子：

\[\begin{align} f_i&=a+bf_i\\ (1-b)f_i&=a\\ f_i&=\frac{a}{1-b} \end{align} \]

　　BZOJ4872

　　XSY2472

分治

　　有一些问题求得是只包含/不包含一个点的情况，只需要考虑当前\([l,r]\)对\([l,mid]\)和\([mid+1,r]\)的影响。

　　下面来讲一道例题

　　\(A(x)\)为\(n-1\)次多项式，\(B_i(x)\)为一次多项式，\(\forall i\)求\(A(x)\mod B_i(x)\)

　　直接做是\(O(n^2)\)的。

　　因为\((A(x)\mod C(x))\mod B_i(x)=A(x)\mod B_i(x)\)（\(C(x)\mod B_i(x)=0\)）

　　设当前已经求出了

\[D_{l,r}=A(x)\mod(\prod_{i=l}^rB_i(x)) \]

　　那么

\[\begin{align} D_{l,mid}&=D_{l,r}\mod(\prod_{i=l}^{mid}B_i(x))\\ D_{mid+1,r}&=D_{l,r}\mod(\prod_{i=mid+1}^{r}B_i(x)) \end{align} \]

　　所以我们可以递归下去做，直到求出所有的\(D_{i,i}\)

　　时间复杂度：

\[T(n)=2T(\frac{n}{2})+O(n\log n)=O(n\log^2n) \]

　　多点求值

　　XSY2469

欧拉phi函数

　　就是\(\varphi\)函数

　　谁都知道这个东西是个积性函数。

\[\varphi(ab)=\varphi(a)\varphi(b)~~~((a,b)=1) \]

　　那如果\((a,b)\neq 1\)呢？

　　设\(d=(a,b)\)

\[\begin{align} \varphi(a)&=a(1-\frac{1}{p1_1})(1-\frac{1}{p1_2})\cdots(1-\frac{1}{p1_{n1}})\\ \varphi(b)&=b(1-\frac{1}{p2_1})(1-\frac{1}{p2_2})\cdots(1-\frac{1}{p2_{n2}})\\ \varphi(ab)&=ab(1-\frac{1}{p3_1})(1-\frac{1}{p3_2})\cdots(1-\frac{1}{p3_{n3}})\\ \varphi(d)&=d(1-\frac{1}{p4_1})(1-\frac{1}{p4_2})\cdots(1-\frac{1}{p4_{n4}}) \end{align} \]

　　可以发现，对于后面那部分

\[\begin{align} (1-\frac{1}{p1_1})(1-\frac{1}{p1_2})\cdots(1-\frac{1}{p1_{n1}})\times (1-\frac{1}{p2_1})(1-\frac{1}{p2_2})\cdots(1-\frac{1}{p2_{n2}})\\ =(1-\frac{1}{p3_1})(1-\frac{1}{p3_2})\cdots(1-\frac{1}{p3_{n3}})\times (1-\frac{1}{p4_1})(1-\frac{1}{p4_2})\cdots(1-\frac{1}{p4_{n4}}) \end{align} \]

　　如果\(p\)只在\(a\)或\(b\)中出现过，那么只会在\(ab\)中出现。如果同时在\(a\)和\(b\)中出现过，那么会同时在\(ab\)和\(d\)中出现。

　　所以有

\[\varphi(ab)=\frac{\varphi(a)\varphi(b)d}{\varphi(d)}~~~(d=(a,b)) \]

逆向思维

情况一

　　有时候我们做某个操作很不好做，我们可以先把所有操作做完后在一个个回复。

　　例如：给以一个图，有两种操作：1.删边；2.询问连通性。

　　我们可以先把需要删的边删掉，再一个个加回来，用并查集维护连通性。

情况二

　　有时候问你\(\forall A\)，满足要求的\(B\)的和。

　　我们可以枚举所有的\(B\)，计算每个\(B\)对每个\(A\)的贡献。

　　AGC005F
　

一类全序问题

　　有\(n\)个物品，你要依次选择这些物品，每个物品有三个属性\(a_i,b_i,c_i\)，当你选择一个物品后，设当前选择的物品的\(c\)属性的和为\(s\)，那么选择这个物品的收益是\(a_i+b_is\)，问你最大收益是多少。

　　假设我们已经钦定了一个顺序。考虑两个相邻的物品（不妨设为前两个），什么时候当前顺序比交换后更优：

\[\begin{align} a_1+a_2+b_2c_1&>a_2+a_1+b_1c_2\\ b_2c_1&>b_1c_2\\ \frac{c_1}{b_1}&>\frac{c_2}{b_2} \end{align} \]

　　这样我们就得到了一个全序关系。

　　那么能不能扩展到任意两个物品的情况呢？

\[\begin{align} a_i+b_ix+a_j+b_j(x+y+c_i)&>a_j+b_jx+a_i+b_i(x+y+c_j)\\ b_jy+b_jc_i&>b_iy+b_ic_j\\ \frac{c_i+y}{b_i}&>\frac{c_j+y}{b_j}\\ \end{align} \]

　　好像并不太行。我们需要换一种思路。

　　假设我们找到了一种最优解，但并不满足以上的性质，那么一定可以交换相邻两个物品使得答案最优。所以直接排序贪心可以得到最优解。

　　如果题目还有其他限制，你也可以在得到这个顺序后DP或者干其他事情。

一类贪心问题

　　有 \(n\) 个怪，组成了一棵树。

　　打一个怪会先扣 \(a_i\) 滴血，在加 \(b_i\) 滴血。

　　怪的父亲要在这个怪之前打。

　　问你初始时最少要有多少血才能把这个怪打完。

　　先不考虑父亲比儿子早选的限制，把所有怪排序。

　　考虑第一个怪，如果可以直接打，就直接打完。

　　否则这个怪会在打完父亲之后立刻打死，就把这个点和父亲合并。

　　题解

　　HDU6326

　　如果要对每个子树求答案的话，可以用平衡树维护操作序列，自底向上合并所有点的操作序列。

　　【集训队作业2018】三角形

莫队

　　总所周知，莫队的时间复杂度和块大小有关。

　　如果块大小为\(t\)，时间复杂度为\(O(\frac{n^2}{t}+mt)\)

　　如果块大小为\(\sqrt n\)，时间复杂度为\(O((n+m)\sqrt n)\)

　　如果块大小为\(\frac{n}{\sqrt{m}}\)，时间复杂度为\(O(n\sqrt m)\)

　　所以有时候可以通过调整块大小来加速。俗称调参。

一类单点修改区间求和的问题

　　有时候我们要修改一个点，求区间和。

算法 修改 求和
树状数组/线段树 \(O(\log n)\) \(O(\log n)\)
分块1 \(O(1)\) \(O(\sqrt n)\)
分块2 \(O(\sqrt n)\) \(O(1)\)

　　树状数组/线段树的做法很经典，这里就不讲了。

　　分块1：每次修改把对应的位置和对应的块的和\(+1\)

　　分块2：每次修改把对应的位置和对应的块的和\(+1\)，然后求出块内前缀和、块内后缀和、块的前缀和。

　　有的人就要问了，分块做法那么慢，有什么用呢？

　　用处大着呢！当修改次数与询问次数不平衡的时候，我们可以做到比树状数组更优。

　　博主曾经用莫队+分块1水过了一道\(n=m={10}^6\)的题。跑的比zjt神犇的线段树合并还快。

和排列有关的问题

　　很多问题让你求对于每一个排列\(A\)，如果\(\cdots\)，那么\(\cdots\)。

　　我们可以考虑从小到大插入这\(n\)个数，插入第\(i\)个数时考虑这个数的贡献。

用trie实现全部数\(+1\)，查询全部数的异或和

　　我们从低位到高位建一棵trie树。

　　从根开始，交换左右子树，然后对\(0\)的那棵子树执行同样的操作（进位）。

莫比乌斯反演

　　有很多题推着推着就推到\(\varphi\)上面去了。

　　说明可以用一条式子：\(\sum_{d|n}\varphi(d)=n\)

莫比乌斯反演的多组询问

\[\begin{align} ans&=\sum_{i=1}^lc^{\gcd(i,b)}\\ &=\sum_{d|s}c^d\sum_{i=1}^l[\gcd(i,s)=d]\\ &=\sum_{d|s}c^d\sum_{i=1}^{\frac{l}{d}}[\gcd(i,\frac{s}{d})=1]\\ &=\sum_{d|s}c^d\sum_{i|\frac{s}{d}}\mu(i)\lfloor\frac{l}{id}\rfloor\\ \end{align} \]

　　看起来没办法化简了

　　这时候要枚举\(j=id\)

\[\begin{align} ans&=\sum_{j|s}\lfloor\frac{l}{j}\rfloor\sum_{i|j}\mu(i)c^\frac{j}{i}\\ \end{align} \]

　　设\(f(x)=\sum_{i|x}\mu(i)c^\frac{x}{i}\)

　　这样\(f(x)\)就可以预处理出来了。
　　

一般情况

\[\begin{align} ans&=\sum_{i=1}^n\sum_{j=1}^mf(\gcd(i,j))\\ &=\sum_{i=1}^{\min(n,m)}f(i)\sum_{i|j}\mu(\frac{j}{i})\lfloor\frac{n}{j}\rfloor\lfloor\frac{m}{j}\rfloor\\ &=\sum_{i=1}^{\min(n,m)}\lfloor\frac{n}{i}\rfloor\lfloor\frac{m}{i}\rfloor\sum_{j|i}f(j)\mu(\frac{i}{j}) \end{align} \]

　　这样可以预处理后面的\(g(n)=\sum_{i|n}\mu(\frac{n}{i})f(i)\)
　　每次枚举前面询问。
　　时间复杂度：\(O(n+T\sqrt{n})\)　　

分治FFT

　　分治FFT一般有两个用途。

求很多个多项式的乘积（普通分治）

　　设有\(n\)个多项式，次数之和是\(m\)，那么时间复杂度就是\(O(m\log m\log n)\)。一共有\(\log n\)层，每层是\(O(m\log m)\)的。

求一类数列（CDQ分治）

　　数列\(f_n=\sum_{i=0}^{n-1}f_ig_{n-i}\)。对于一个分治区间\([l,r]\)，先求出\([l,mid]\)的答案，再计算这部分对右边\([mid+1,r]\)的贡献。

　　时间复杂度：\(O(n\log^2 n)\)

组合数学

\[\sum_{i=j}^{n-k}\binom{i}{j}\binom{n-i}{k}=\binom{n+1}{j+k+1} \]

　　可以用插板法理解。

树上的连通块

　　树上连通块个数\(=\)点数\(-\)边数。

　　点数/边数中一般有一个是固定的。

轻重链剖分&长链剖分

轻重链剖分

　　每个重链顶端的子树大小总和是 \(O(n\log n)\) 的。

　　每个点到根经过的轻边个数是 \(O(\log n)\) 的。

　　适用于维护与树的大小有关的信息。

长链剖分

　　每个长链顶端的子树深度总和是 \(O(n)\) 的。

　　适用于维护与树的深度有关的信息。

高维前缀和 & 莫比乌斯反演

　　复杂度为 \(O(\sum_{i}\frac{n}{p_i})=O(n\log log n)\)

\[g(n)=\sum_{d\mid n}f(d) \]

for(int i=1;i<=cnt;i++)
    for(int j=1;j*pri[i]<=n;j++)
        f[j*pri[i]]+=f[j];

\[g(n)=\sum_{n\mid d}f(d) \]

for(int i=1;i<=cnt;i++)
    for(int j=n/pri[i];j>=0;j--)
        f[j]+=f[j*pri[i]];

\[g(n)=\sum_{d\mid n}f(d)\mu(\frac{n}{d}) \]

for(int i=1;i<=cnt;i++)
    for(int j=n/pri[i];j>=0;j--)
        f[j*pri[i]]-=f[j];

\[g(n)=\sum_{n\mid d}f(d)\mu(\frac{d}{n}) \]

for(int i=1;i<=cnt;i++)
    for(int j=1;j*pri[i]<=n;j++)
        f[j]-=f[j*pri[i]];

网络流

　　如果要的是最大收益，那么可以先强制选所有正的边，然后把不选一条边看成割掉这条边，答案为正的边权和 \(-\) 最小割。

流量平衡

　　可以先对于每条边钦定一个方向，然后如果一条边有流量就表示这条边改了方向。对于一个点 \(i\)，要根据出度入度的关系向源/汇连边。

网格图

　　把每一行看做一个点，把每一列看做一个点，选一个格子就在对应的行列之间连边。

　　这是一个分层图，用 dinic 跑会比较快。

一种限制

　　每个物品对应一条链，割一条边代表这个物品对应的数/放在什么位置。

　　\(i\) 对应的链割了点 \(x\) 后面的边时 \(j\) 对应的链必须割点 \(y\) 后面的边

　　解决方法为连边 \((x,y,\infty)\)。

　　

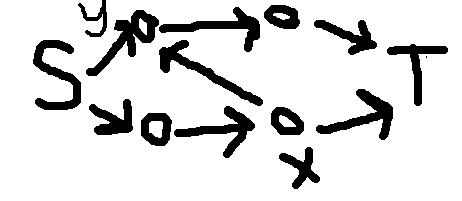
　　有时候限制是 \(i\) 割了点 \(x\) 后面的边时 \(j\) 必须割点 \(y\) 前面的边

　　那么就要把一边的链反过来。

　　常见的方法有：

　　　横着的链不变，竖着的链反过来。

　　　黑白染色，白色的点对应的链不变，黑色的点对应的链反过来。

　　要注意前面的点属于 T 集且后面的点属于 S 集的情况。

　　要从后面的点往前面的点连容量为 \(\infty\) 的边。

　　BZOJ3144切糕

原图中不能有 \(S\to T\to S\) 的路径

　　把所有反向边的容量设为 \(\infty\) 即可。

点分树

　　二叉树的点分树中每个节点只有至多 \(3\) 个儿子。这样可以直接可持久化这棵点分树，可以减少一个 \(\log\)（把点分树当成三叉数可持久化，深度是 \(\log\) 的）。

　　如果题目给的树不是二叉树，可以强行转成二叉树。

最小树形图

　　用可合并堆维护每个点的最小入边，可以做到 \(O(n+m)\log m\)

容斥方法 总结

每次在剩下的物品中选一种拿走一个，求拿走的最后一个物品是第一种物品的概率 的问题

　　考虑容斥，枚举哪些物品是在第一种物品拿完之后拿走的（剩下的随意）。

　　那么剩下的物品就可以忽略了，只需要求出第一种物品是第一个拿完的概率。

　　对于 【UNR #3】百鸽笼 这道题，可以DP

　　　考虑拿走第一种物品时每种物品拿了几个，就可以DP了：

　　　设 \(f_{i,j,k}\) 表示考虑完了前 \(i\) 种物品，有 \(j\) 种要在第一种取完之后才取完，已经取了 \(k\) 个物品。

　　　最终长度为 \(l\) ，取了 \(j\) 种的序列的序列的贡献是 方案数 \(\times {(-1)}^j\times {(\frac{1}{j+1})}^l\)

　　对于 【PKUWC2018】猎人杀 这道题，第一种物品是第一个取完的概率是 \(\frac{w_1}{\sum w_i}\)。可以用分治 NTT 计算方案数。

有 \(m\) 种颜色的球排成一行，共 \(n\) 个，求最终有 \(k\) 个同色的球相邻的方案数

　　先假设每种球分成几段，然后用分治 FFT 算出方案数。

　　但是这样可能会有相邻且同色的段

　　这时候就可以容斥了。

　　考虑每种方案把相邻且同色的段合并之后有几段

　　那么就有

\[\begin{align} ans_i&=g_i−\sum{j<i}ans_{j}\binom{m−j}{i−j}\\ &=\sum_{j\leq i}g_j{(-1)}^{i-j} \end{align} \]

　　https://www.cnblogs.com/ywwyww/p/8513349.html

有 \(m\) 种颜色的球排成一行，共 \(n\) 个，最终贡献和同色段长度有关的

　　先算出每种长度的贡献

　　假设想分成 \(i\) 段，但最终分成了 \(j\) 段，那么此时的容斥系数是 \({(-1)}^{i-j}\)，方案数是 \(\binom{i-1}{j-1}\)

　　然后拿最终分成的段数去跑 DP 就好了。

　　https://www.cnblogs.com/ywwyww/p/9279670.html

和树上两点间路径长度有关的技术&其他问题

　　比如说树上长度不超过 \(k\) 的路径数量 等等

　　现在主要有三种方法：

点分治/点分治树

平衡树合并/线段树合并

长链剖分

　　这里讲几道题吧

问题\算法 点分治 平衡树合并 长链剖分
树上长度不超过 \(k\) 的路径条数（无边权） \(O(n\log n)\) \(O(n\log n)\) \(O(n)\)
LOJ571 \(O(n\log^2n)\) \(O(n\log^2n)\) \(O(n\log n)\)
[WC2010]重建计划 \(O(n\log n\log V)\) \(O(n\log n\log V)\) \(O(n\log V)\)

ZKW 费用流中处理掉负权的方法

　　先用 SPFA 跑一边最短路，处理出 \(S\) 到每个点的距离 \(d_i\)

　　显然对于每一条边 \((u,v,w)\) 都有 \(d_u+w\geq d_v\)

　　对于一条边 \((u,v,w)\)，把这条边的边权变为 \(w'=w+d_u-d_v\)。这样整个图中就没有负权了。

　　容易证明在新图上跑出的最短路就是原图的最短路，只是长度有一点变化：\(d'_T=0\)

　　所以后面原点到汇点的距离要加上 \(d_T\)

用 dijkstra 代替 bellman-ford 跑费用流

　　还是先处理出 \(S\) 到每个点的距离 \(d_i\)。

　　还是把每条边的边权变为 \(w'=w+d_u-d_v\)。

　　因为新建的反向边一定满足 \(d_u+w_{u,v}=d_v\)，所以 \(w_{v,u}'=-w_{u,v}+d_v-d_u=0\)

　　新图的最短路还是比原图的最短路少了 \(d_T\)

单位根反演（求和引理）

　　在碰到

\[\sum_{i=0}^n\binom{n}{i}a^ib^{n-i}[k\mid i] \]

　　时可以用求和引理优化：

\[\begin{align} [k\mid i]&=\frac{1}{k}\sum_{j=0}^{k-1}w_k^{ij}\\ &~~~~\sum_{i=0}^n\binom{n}{i}a^ib^{n-i}[k\mid i]\\ &=\sum_{i=0}^n\binom{n}{i}a^ib^{n-i}\frac{1}{k}\sum_{j=0}^{k-1}w_k^{ij}\\ &=\frac{1}{k}\sum_{j=0}^{k-1}\sum_{i=0}^n\binom{n}{i}a^ib^{n-i}w_k^{ij}\\ &=\frac{1}{k}\sum_{j=0}^{k-1}{(aw_k^j+b)}^n \end{align} \]

prufer 序列

　　\(K_{n,m}\) 的生成树个数是 \(n^{m-1}m^{n-1}\)

　　\(K_{n_1,n_2,\ldots,n_k}\) 的生成树个数是 \(n^{k-2}\prod_{i=1}^k{(n-n_i)}^{n_i-1}\)，其中 \(n=\sum_{i=1}^kn_i\)

　　有一个 \(n\) 个点，\(m\) 个连通块，每个连通块大小为 \(a_i\) 的森林。你要加上若干条边，让这个森林变成一棵树。方案数为

\[\sum_{\sum_{i=1}^m d_i=2(m-1)}(m-2)!\prod_{i=1}^m\frac{a_i^{d_i}}{(d_i-1)!}\\ =n^{m-2}\prod_{i=1}^ma_i \]

树形DP

　　\(f_{i,j}\) 为以 \(i\) 为根的子树，选出来的点数为 \(j\) 时的方案数/贡献。这里 \(j\leq k\)。

　　转移时要枚举两边各选了多少点。直接做是 \(O(nk^2)\) 的。

　　注意到当选的点数 \(\leq size\) 时才有意义。这样转移时两棵子树选的点数可以只枚举到 \(\min(size,k)\)，这样就是 \(O(nk)\) 的了。

　　证明：
　　　1.两棵子树大小都 \(>k\)。只有 \(O(\frac{n}{k})\) 次转移，复杂度为 \(O(\frac{n}{k}\times k^2)=O(nk)\)。
　　　2.一棵子树大小 \(\leq k\)，另一颗子树大小 \(>k\)。对于所有的这类转移，小的那棵子树的大小之和是 \(O(n)\) 的。复杂度为 \(O(n\times k)=O(nk)\)。
　　　3.两棵子树大小都 \(\leq k\)。把所有这类转移在树上标出来，那么会标出很多棵子树。每棵子树复杂度为 \(O({size}^2)\)，其中 \(size\leq 2k\)。复杂度为 \(O(nk)\)。

　　这样总的复杂度就是 \(O(nk)\) 了。

用全局平衡二叉树优化链剖+NTT

　　如果 \(f_x\) 的次数 \(x\) 子树的深度有关，就可以直接长链剖分+分治NTT做到 \(O(n\log^2n)\)。

　　否则就要用重链剖分+分治NTT。复杂度为 \(O(n\log^3n)\)。

　　但是我们可以在全局平衡二叉树上面合并。

　　一个点 \(x\) 有 \(size_{ls}\leq \frac{1}{2}size_x,size_{rs}\leq \frac{1}{2}size_x,\max(size_v)\leq \frac{1}{2}size_x\)（这里 \(v\) 是 \(x\) 的轻儿子（虚儿子））。

　　这样只会跳 \(O(\log n)\) 次实边。

　　那虚边呢？

　　如果是和子树深度有关的题，直接把 \(f_v\) 加起来就好了。总复杂度为 \(O(n\log^2n)\)

　　如果是和子树大小有关的题，可以再用一次全局平衡二叉树的思想：找到一个点 \(v\) 满足 \(size_{ls}\leq \frac{1}{2}\sum size_v,size_{rs}\leq \frac{1}{2}\sum size_v\)，但是中间那个儿子的 \(size_y\) 可能会 \(>\frac{1}{2}\sum size_v\)。但这并不影响复杂度，因为 \(size_y<\frac{1}{2}size_x\)，所以从一个点的某个虚儿子 \(v\) 跳到 \(x\) 需要的步数是 \(O(\log\frac{\sum size_v}{size _v}+1)=O(\log \frac{size_x}{size_v})\)。所以总的复杂度就是 \(O(n\log^2n)\)。

DP优化

　　记 \([l_i,r_i]\) 为 \(i\in g(k-1)\) 可以转移到的 \(g(k)\) 中的区间（或者能转移到 \(g(k)\) 的区间）。要求任意两个 \([l_i,r_i],[l_j,r_j]\) 不互相严格包含。（这里严格包含指的是包含且左端点不同且右端点不同）
　　我们可以把 \(g(k)\) 切成若干个区间，满足 \([l_i,r_i]\) 不被任意一个区间严格包含，且 \([l_i,r_i]\) 最多与两个区间相交。
　　方法如下：对于一个区间的左端点，找到最右的右端点使得这个区间不严格包含任何 \([l_i,r_i]\)。可以证明，这个方法满足条件。
　　这样，一个 \([l_i,r_i]\) 一定是一个区间的前缀或后缀，分两部分DP一下就好了。DP过程类似决策单调性优化DP。

区间加&区间 \(\gcd\)

\[\gcd(a_1,a_2,\ldots,a_n)=\gcd(a_1,a_2-a_1,a_3-a_2,a_4-a_3,\ldots,a_n-a_{n-1}) \]

　　维护差分后的序列即可。

数位DP

　　有时候会遇到很多个数的和 \(\leq m\)，每个数 \(\leq n\)，还有一些其他限制的计数题。
　　可以从低位往高位数位DP，记录进位和只考虑低位的大小关系。

posted @ 2018-03-05 21:28  ywwyww  阅读(5233)  评论(6)  编辑  收藏  举报