图
| 这个作业属于哪个班级 |
| ---- | ---- | ---- |
| 这个作业的地址 |
| 这个作业的目标 | 学习图结构设计及相关算法 |
|姓名|喻文康|
0.PTA得分截图

1.本周学习总结
1.1 图的存储结构
1.1.1 邻接矩阵
图:
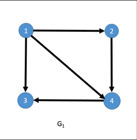
对应邻接矩阵:
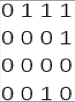
结构体定义:
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,弧数
} MGraph; //图的邻接矩阵表示类型
建图函数:
void CreateMGraph(MGraph& g, int n, int e)//建图
{
int i, j;
g.n = n;
g.e = e;
for (i = 0; i <= g.n; i++) //初始化邻接矩阵
for (j = 0; j <= g.n; j++)
g.edges[i][j] = 0;
for (i = 0; i < g.e; i++)
{
int n, m ;
cin >> n >> m; //修改邻接矩阵中的值
g.edges[n][m] = 1;
g.edges[m][n] = 1;
}
}
1.1.2 邻接表
图:
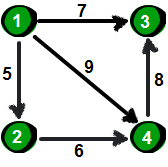
对应邻接矩阵:
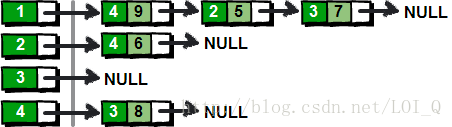
结构体定义:
#define MAX_VERTEX_NUM 10 /*定义最大顶点数*/
typedef int Vertex;
typedef struct ArcNode{ /*表结点*/
int adjvex; /*邻接点域*/
struct ArcNode *nextarc; /*指向下一个表结点*/
}ArcNode;
typedef struct VNode{ /*头结点*/
Vertex data; /*顶点域*/
ArcNode *firstarc; /*指向第一个表结点*/
}VNode,AdjList[MAX_VERTEX_NUM]; /*AdjList是数组类型*/
typedef struct {
AdjList vertices; /*邻接表中数组定义*/
int vexnum,arcnum; /*图中当前顶点数和边数*/
} ALGraph; /*图类型*/
建图函数:
void CreateAdj(AdjGraph *&G,int n,int e) //创建图邻接表
{
int i,j,a,b;
ArcNode *p;
G=new AdjGraph;
for (i=0;i<n;i++) G->adjlist[i].firstarc=NULL;
for (i=1;i<=e;i++) //根据输入边建图
{
cin>>a>>b; //有向图
p=new ArcNode; //创建一个结点p
p->adjvex=b; //存放邻接点
p->nextarc=G->adjlist[a].firstarc; //采用头插法插入结点p
G->adjlist[a].firstarc=p;
}
G->n=n; G->e=n;
}
1.1.3 邻接矩阵和邻接表表示图的区别
①对于任一确定的无向图,邻接矩阵是唯一的(行列号与顶点编号一致),但邻接表不唯一(链接次序与顶点编号无关)。
②邻接矩阵的空间复杂度为0(n2),而邻接表的空间复杂度为0(n+e)。
③在邻接表上容易找到任意一顶点的第一个邻接点和下一个邻接点,但要判定任意两个顶点(vi,vj)之间是否有边或弧相连,则需搜索第i个或第j个链表,还不及邻接矩阵方便。
④邻接矩阵多用于稠密图的存储(e接近n(n-1)/2),而邻接表多用于稀疏图的存储(e<<n2)。
1.2 图遍历
1.2.1 深度优先遍历
邻接表图的深度遍历结果(从1开始):

深度遍历代码:
void DFS(ALGraph *G, int i) {
cout<<i;
visited[i] = 1;
struct ArcNode * w;
for ( w= G->vertices[i].firstarc;w;w=w->nextarc) {
if (visited[w->adjvex] == 0)
DFS(G, w->adjvex);
}
}
1.2.2 广度优先遍历
邻接表图的广度遍历结果(从1开始):
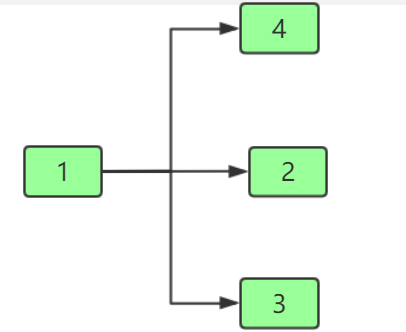
广度遍历代码:
void BFS(ALGraph *G,int v)
{
int que[10];
int front,rear;
front= rear = 0;
cout<<v;
visited[v] = TRUE;
que[rear++] = v;
while(rear!=front)
{
int i = que[front++];
ArcNode *tmp = G->vertices[i].firstarc;
while(tmp)
{
if(!visited[tmp->adjvex])
{
printf(" %d",tmp->adjvex);
visited[tmp->adjvex] = TRUE;
que[rear++] = tmp->adjvex;
}
tmp = tmp->nextarc;
}
}
}
1.3 最小生成树
什么是最小生成树:
如果是不带权值的图的最小生成树,那么它包含原图中的所有 n 个结点,并且有保持图连通的最少的边
如果是带权值的图的最小生成树,那么它就是包含原图中的所有 n 个结点,并且所以边的权值的累加和最小
有些图的最小生成树不唯一
1.3.1 Prim算法求最小生成树
算法思想:
1.先选择一个顶点作为树的根节点,把这个根节点当成一棵树
2.选择图中距离这棵树最近但是没有被树收录的一个顶点,把他收录在树中,并且保证不构成回路
3.按照这样的方法,把所有的图的顶点一一收录进树中。
4.如果没有顶点可以收录
a.如果图中的顶点数量等于树的顶点数量-->最小生成树构造完成
b. 如果图中的顶点数量不等于树的顶点数量-->此图不连通
算法过程
1.将一个图的顶点分为两部分,一部分是最小生成树中的结点(A集合),另一部分是未处理的结点(B集合)。
2.首先选择一个结点,将这个结点加入A中,然后,对集合A中的顶点遍历,找出A中顶点关联的边权值最小的那个(设为v),将此顶点从B中删除,加入集合A中。
3.递归重复步骤2,直到B集合中的结点为空,结束此过程。
4.A集合中的结点就是由Prime算法得到的最小生成树的结点,依照步骤2的结点连接这些顶点,得到的就是这个图的最小生成树。
图解

基于上述图结构求Prim算法生成的最小生成树的边序列:
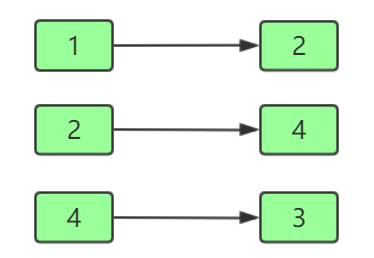
实现Prim算法的2个辅助数组是什么?其作用是什么?:
两个辅助数组:closest[i]数组和lowcost[i]数组
closest[i]:最小生成树的边依附在U中顶点编号。
lowcost[i]:表示顶点i (iEV一U)到U中顶点的边权重,取最小权重的项点k加入U。并规定lowcost[k]=O表示这个顶点在U中
Prim算法代码:
#define INF 32767 //INF表示oo
void Prim(MGraph g, int v)
{
int lowcost[MAXV], min, closest[MAXV], i, j, k;
for (i = 0; i < g.n; i++) //给lowcost[]和closest[]置初值
{
lowcost[i] = g.edges[v][i];
closest[i] = v;
}
for (i = 1; i < g.n; i++) //找出(n-1)个顶点
{
min = INF;
for (j = 0; j < g.n; j++)//在(V-U)中找出离U最近的顶点
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j]; k = j; //k记录最近顶点的编号
}
printf("边(%d,%d)权为:%d\n", closest[k], k, min);
lowcost[k] = 0; //标记k已经加入U
for (j = 0; j < g.n; j++) //修改数组lowcost和closest
if (g.edges[k][j] != 0 && g.edges[k][i] < lowcost[j] // 修正
{
lowcost[j] = g.edges[k][i];
closest[j] = k;
}
}
}
时间复杂度:O(n平方)
适用邻接矩阵图结构
1.3.2 Kruskal算法求解最小生成树
算法思想:
使用贪心算法,每次获取权重最小的边,但是不能让生成树构成回路。直到去到V-1条边为止。
算法过程
1.将图各边按照权值进行排序
2.将图遍历一次,找出权值最小的边,(条件:此次找出的边不能和已加入最小生成树集合的边构成环),若符合条件,则加入最小生成树的集合中。不符合条件则继续遍历图,寻找下一个最小权值的边。
3.递归重复步骤1,直到找出n-1条边为止(设图有n个结点,则最小生成树的边数应为n-1条),算法结束。得到的就是此图的最小生成树。
图解
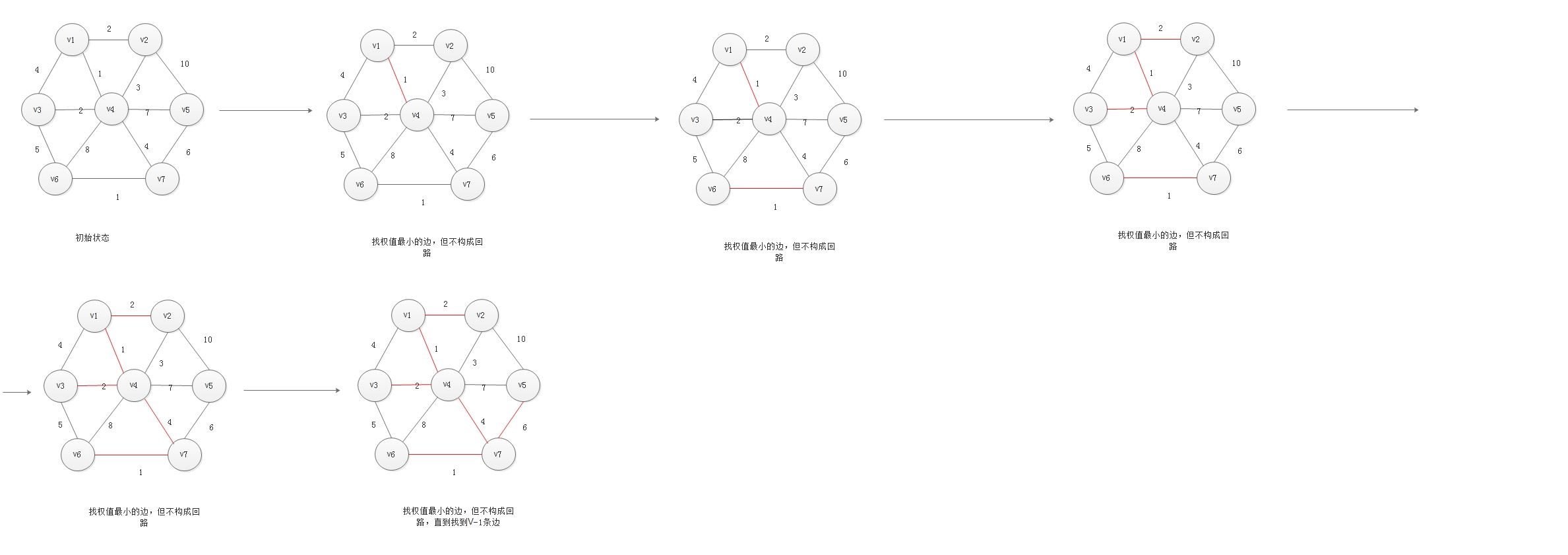
基于上述图结构求Kruskal算法生成的最小生成树的边序列:

实现Kruskal算法的辅助数据结构是什么?其作用是什么?
1.线性结构:图中边的存储需要定义边数组存放
2.图结构:图存放各顶点信息以及每条边的信息,图要用邻接表来存储更适合
Kruskal算法代码
void Kruskal(AdjGraph* g)
{
int i, j,u1,v1,sn1,sn2,k;
int vset[MAXV]; // 集合辅助数组
Edge E[MaxSizel; //存放所有边
k=0; //E数组的下标从0开始计
for (i = 0; i < g.n; i++) // 由g产生的边集E
{
p = g->adjlist[i].firstarc;
while (p != NULL)
{
E[k].u = i;
E[k].v = p->adjvex;
E[k].w = p->weight;
k++; p = p->nextarc;
}
InsertSort(E,g.e); //用直接插入排序对E数组按权值递增排序
for (i = 0; i < g.n; i++)//初始化辅助数组
vset[i] = i;
k = 1;//k表示当前构造生成树的第几条边,初值为1
j = 0;//E中边的下标,初值为0
while (k < g.n)//生成的顶点数小于n时循环
{
u1 = E[j].u; v1 = E[j].v;// 取一条边的头尾顶点
sn1 = vset[u1];
sn2 = vset[v1];//分别得到两个顶点所属的集合编号
if (sn1 != sn2)//两顶点属于不同的集合
{
printf(" (%d,%d):%d\n", u1,v1,E[].w);
k++;// 生成边数增1
for (i = 0; i < g.n; i++)// 两个集合统一编号
if (vset[i] == sn2)//集合编号为sn2的改为sn1
vset[i] = sn1;
}
j++;//扫描下一条边
}
}
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
Dijkstra算法是针对单源点求最短路径的算法。
其主要思路如下:
-
将顶点分为两部分:已经知道当前最短路径的顶点集合Q和无法到达顶点集合R。
-
定义一个距离数组(distance)记录源点到各顶点的距离,下标表示顶点,元素值为距离。源点(start)到自身的距离为0,源点无法到达的顶点的距离就是一个大数(比如Infinity)。
-
以距离数组中值为非Infinity的顶点V为中转跳点,假设V跳转至顶点W的距离加上顶点V至源点的距离还小于顶点W至源点的距离,那么就可以更新顶点W至源点的距离。即下面distance[V] + matrix[V][W] < distance[W],那么distance[W] = distance[V] + matrix[V][W]。
-
重复上一步骤,即遍历距离数组,同时无法到达顶点集合R为空。
Dijkstra算法如何解决贪心算法无法求最优解问题
在每次循环结束前都要对path[]数组和dist[]数组进行调整
for (j = 0; j < g.n; j++)//修改不在s中的顶点的距离
{
if (s[j] == 0)
if (g.edges[u][j] < INF && dist[u] + g.edges[u][i] < dist[j])
{
dist[j] = dist[u] + g.edges[u][j];
path[j] = u;
}
}
Dijkstra算法的时间复杂度,使用什么图结构,为什么
算法时间复杂度为O(n的平方),图存储结构为邻接矩阵,因为每次都要访问图里的数据,用邻接矩阵更高效。
1.4.2 Floyd算法求解最短路径
Floyd算法(Floyd-Warshall algorithm)又称为弗洛伊德算法、插点法,是解决给定的加权图中顶点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
适用范围:无负权回路即可,边权可正可负,运行一次算法即可求得任意两点间最短路。
优缺点
Floyd算法适用于APSP(AllPairsShortestPaths),是一种动态规划算法,稠密图效果最佳,边权可正可负。此算法简单有效,由于三重循环结构紧凑,对于稠密图,效率要高于执行|V|次Dijkstra算法。
优点:容易理解,可以算出任意两个节点之间的最短距离,代码编写简单
缺点:时间复杂度比较高,不适合计算大量数据。
时间复杂度:O(n3);空间复杂度:O(n2);
1.5 拓扑排序
在一个有向图中,对所有的节点进行排序,要求没有一个节点指向它前面的节点。
先统计所有节点的入度,对于入度为0的节点就可以分离出来,然后把这个节点指向的节点的入度减一。
一直做改操作,直到所有的节点都被分离出来。
如果最后不存在入度为0的节点,那就说明有环,不存在拓扑排序,也就是很多题目的无解的情况。
演示图
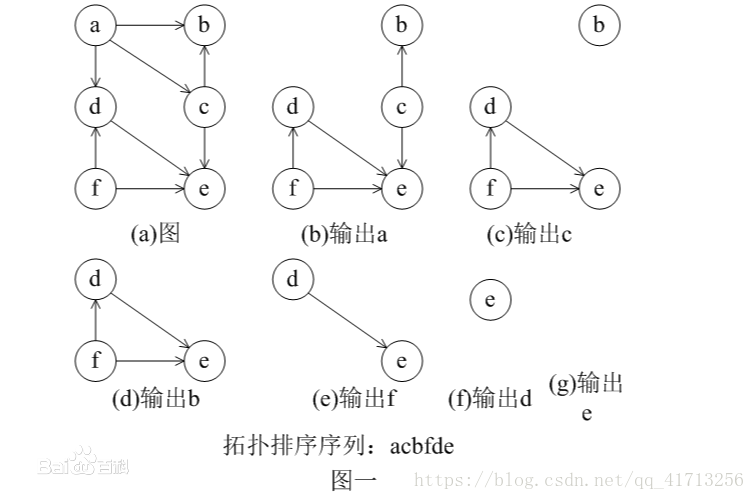
拓扑排序伪代码
遍历邻接表
计算每个顶点的入度,存入头结点count成员遍历图顶点
若发现入度为0顶点,入栈st
while (栈不空)
{
出栈节点v,访问。
遍历v的所有邻接点
{
所有邻接点的入度 - 1
若有邻接点入度为0,则入栈st
}
}
拓扑排序代码
void TopoSort(ALGraph* G, int n)
{
int i, j, k, top, m = 0;
EdgeNode* p;
int* d = (int*)malloc(n * sizeof(int));
for (i = 0; i < n; i++) //初始化数组
{
d[i] = 0;
}
for (i = 0; i < n; i++) //统计各个顶点的入度情况,并把他们填入数组里面
{
p = G->adjlist[i].firstedge;
while (p != NULL)
{
j = p->adjvex;
d[j]++;
p = p->next;
}
}
top = -1;
for (i = 0; i < n; i++) //先找出里面入度是0的顶点
{
if (d[i] == 0)
{
d[i] = top;
top = i;
}
}
while (top != -1)
{
j = top;
top = d[top];
printf("%d ", j);
m++; //统计顶点
p = G->adjlist[j].firstedge;
while (p)
{
k = p->adjvex; //相l连接的顶点
d[k]--; //相连接的顶点入度减1
if (d[k] == 0) //如果发现入度为0的新顶点,从该顶点出发
{
d[k] = top;
top = k;
}
p = p->next;
}
}
if (m < n) printf("\n有回路!\n");
free(d);
}
1.6 关键路径
1.6.1 什么叫AOE-网
- 在现代化管理中,人们常用有向图来描述和分析一项工程的计划和实施过程,一个工程常被分为多个小的子工程,这些子工程被称为活动(Activity),在带权有向图中若以顶点表示事件,有向边表示活动,边上的权值表示该活动持续的时间,这样的图简称为AOE网
1.6.2 什么是关键路径概念
- 关键路径是指设计中从输入到输出经过的延时最长的逻辑路径。优化关键路径是一种提高设计工作速度的有效方法
1.6.3 什么是关键活动?
-
关键活动是为准时完成项目而必须按时完成的活动。即处于关键路径上的活动。所有项目都是由一系列活动组成,而在这些活动中存在各种链接关系和活动约束。其中有些活动如果延误就会影响整个项目工期。在项目中总存在这样一类直接影响项目工期变化的活动,这些活动就是关键活动。
-
另外,还有次关键活动,次关键活动亦称“准关键活动”。在次关键路径上的活动。即总时差短或时差很小的活动。其路长仅次于关键路径路长。与之对应的还有关键活动和松弛活动。关键活动指处于关键路径上的任何活动,而松弛活动指具有很大时差的活动。
2.PTA实验作业
2.1 六度空间
2.1.1 解题思路(伪代码)
建立邻接表g,遍历g
visited[]判断结点,访问为1,否为0
q.push(x)//先将x放入队列中
visited[x]=0;
while(!q.enmpty())//当q不为空时
{
temp=q.front();
p访问q中队头所对应的邻接表结点
q.pop();
while(p!=NULL)
{
如果p未被访问 {入队,这样子当访问到最后该层的最后一个结点时,储存的会是下一层最后一个结点的位置 }
p=p->nextarc 访问p的下一个邻接点
}
if(temp=last) 此时找到了下一层结点的最后一个元素位置,将其值给last}
}
return sum
2.1.2 提交列表

2.1.3 本题知识点
- 1.首先需要图的创建(邻接表/邻接矩阵)
- 2.图的广度搜索bfs遍历图结构
- 3.队列的用法及队列各函数的作用
2.2 村村通
2.2.1 解题思路(伪代码)
最小堆存边结点,然后直接用kruskal建最小生成树的思想累计成本,用并查集判断结点间是否连通
就是对每一个已经入队的点一个一个遍历寻找下一个最短路径
但是,更好的方法是对每一个点入队,更新到未入队的点的最短距离。就是,距离比原先的距离小,就更新。
这样每次对每个点更新那么就能保证lowCost中的距离在当前状态下就是最小的
然后每次让距离最短的入队就可以了
2.2.2 提交列表

2.2.3 本题知识点
- 1.能够用邻接矩阵建图
- 2.能够使用prime算法或kruskal算法求最短路径


 浙公网安备 33010602011771号
浙公网安备 33010602011771号