机器学习之贝叶斯算法

# coding = utf-8
from sklearn.naive_bayes import MultinomialNB
from sklearn.datasets import load_iris, fetch_20newsgroups, load_boston
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.ensemble import RandomForestClassifier
import pandas as pd

'''
特征之间相互独立
联合概率：P(A,B) = P(A)*P(B)  关键字“且”
条件概率：就是事件A在另一个时间B已经发生的条件下发送的概率 记，P(A|B)
    特性：P(A1,A2|B) = P(A1|B)*P(A2|B) ,A1,A2必须相互独立

朴素贝叶斯：P(C|W) = ( P(W|C)*P(C) )/ P(W),C为文档类别，W为给定文档特征值


解决计算结果为0：
    拉普拉斯平滑：拉普拉斯平滑系数
    P(F1|C) = (Ni+a) / (N+am) ,其中a为指定的系数，一般为1;m为训练文档中统计的特征词个数


API:sklearn.naive_bayes import MultinomialNB(a=1.0)


朴素贝叶斯：
    优势：理论基础；对缺失数据不敏感；分类准确率高，速度快
    影响因素：数据中特征词的选择是否合理
    参数：没有超参可以调
    场景：文本分类
'''


def naviebyte():
    """
    朴素贝叶斯
    :return:
    """
    #数据抽取
    news = fetch_20newsgroups(subset='all')


    #数据分割
    x_train,x_test,y_train,y_test = train_test_split(news.data,news.target,test_size=0.25);

    #对数据集进行特征抽取
    tf = TfidfVectorizer()

    #以训练集当中的词列表进行每篇文章重要性统计
    x_train = tf.fit_transform(x_train)

    print(tf.get_feature_names())

    x_test = tf.transform(x_test)


    #贝叶斯实例化
    mlt = MultinomialNB(alpha=1.0)
    print(x_train.toarray())
    #训练
    mlt.fit(x_train,y_train)
    #预测
    y_predict = mlt.predict(x_test)
    print("预测的文章类别为：",y_predict)
    #准确率
    print("准确率为：",mlt.score(x_test,y_test))

    return  None


if __name__ == '__main__':
    naviebyte()

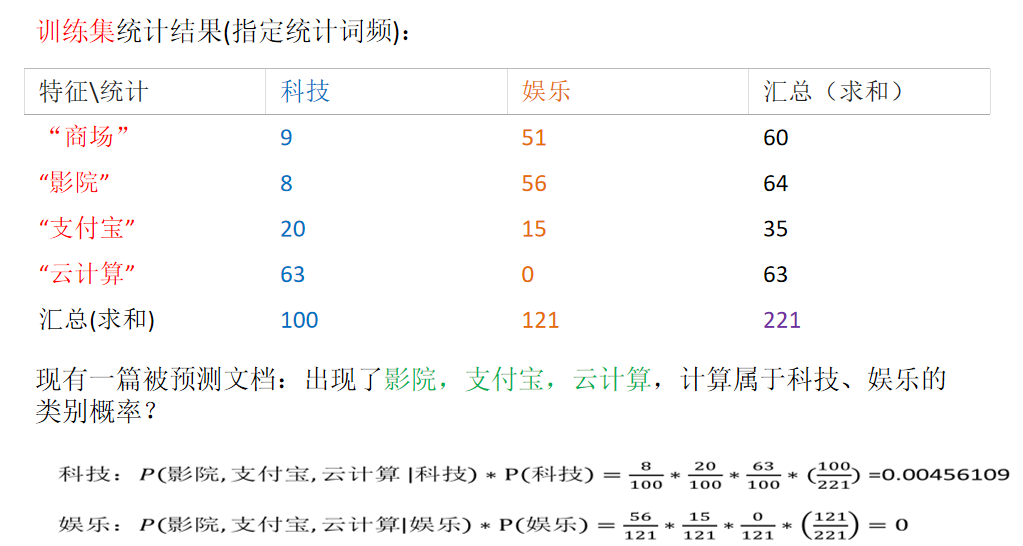
计算方法：