tarjan算法与无向图的连通性(割点,桥,双连通分量,缩点)
基本概念
给定无向连通图G = (V, E)
割点:
对于x∈V,从图中删去节点x以及所有与x关联的边之后,G分裂为两个或两个以上不相连的子图,则称x为割点
割边(桥)
若对于e∈E,从图中删去边e之后,G分裂成两个不相连的子图,则称e为G的桥或割边
时间戳
在图的深度优先遍历过程中,按照每个节点第一次被访问的时间顺序,依次给予N个节点1~N的整数标记,该标记被称为“时间戳”,记为dfn[x]
搜索树
在无向连通图中任选一个节点出发进行深度优先遍历吗,每个节点只访问一次。所有发生递归的边(x, y)构成一棵树,称为“无向连通图的搜索森林”。一般无向图的各个连通块的搜索树构成无向图的“搜索森林”。对于深度优先遍历出的搜索树,按照被遍历的次序,标记节点的时间戳
追溯值
追溯值low[x]。设subtree(x)表示搜索树中以x为根的子树。low[x]定义为以下节点时间戳的最小值
low[u]定义为u或者u的子树中能够通过非父子边(父子边就是搜索树上的边)追溯到的最早的节点的时间戳
即:
1.subtree(x)中的节点
2.通过一条不在搜索树上的边,能够到达subtree(x)的节点
为了计算low[x],应该先令low[x] = dfn[x],然后考虑从x出发的每条边(x, y):
若在搜索树上x是y的父节点,则令low[x] = min(low[x], low[y])
若无向边(x, y)不是搜索树上的边,则令low[x] = min(low[x], dfn[y])
桥的判定法则
无向边(x, y)是桥,当且仅当搜索树上存在x的一个子节点y,满足:
dfn[x] < low[y]
根据定义,dfn[x] <low[y]说明从subtree(y)出发,在不经过(x, y)的前提下,不管走哪条边,都无法到达x或比x更早访问的节点。若把(x, y)删除,则subtree(y)就好像形成了封闭的环境,与节点x没有边相连,图断成了两部分,(x, y)为桥
反之,若不存在这样的子节点x和y,使得dfn[x] < low[y],这说明每个subtree(y)都能绕行其他边到x或比x更早的节点,(x, y)也就不是桥
桥一定是搜索树中的边,并且一个简单环中的边一定都不是桥
需要注意的是, 因为我们要遍历的是无向图, 所以从每个节点x出发,总能访问到他的父节点fa,根据low的计算方法,(x, fa)属于搜索树上的边,且fa不是x的子节点,故不能用fa的时间戳来更新low[x]。
如果仅记录每个节点的父节点,会无法处理重边的情况——当x与fa之间有多条边时,(x, fa)一定不是桥,在这些重复计算中,只有一条边在搜索树上,其他的几条都不算,故有重边时,dfn[fa]不能用来更新low[x]
解决方案是:记录“递归进入每个节点的边的编号”。编号可认为是边在邻接表中储存下标位置。把无向图的每条边看做双向边,成对存储在下标"2和3","4和5","6和7"...处。若沿着编号i的边递归进入节点x,则忽略从x出发的编号为i xor 1的边,通过其他边计算low[x]即可
(补充:^的成对变换
对于非负整数n
当n为偶数时,n xor 1等于n+1
当n为奇数时,n xor 1等于n-1
因此“0与1”“2与3”“3与5”……关于xor 1运算构成了成对变换
这一性质经常用于图论邻接表中边集的存储。在具有无向边(双向边)的图中把一对正反方向的边分别储存在邻接表数组的第n与n+1个位置(其中n为偶数),就可以通过xor 1运算获得与当前边(x, y)反向的边(y, x)的存储位置
在程序开始时,初始化变量tot = 1。这样每条无向边看成的两条有向边会成对存储在ver和edge数组的下表“2和3”“4和5”“6和7”……的位置上。通过对下表xor 1操作,就可以直接定位到与当前反向的边。换句话说,如果ver[i]是第i条边的终点,那么ver[i ^ 1]就是第i条边的起点)

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn = 100086; 4 struct node { 5 int y, net; 6 }e[maxn << 1]; 7 int lin[maxn], len = 1; 8 bool bridge[maxn << 1]; 9 int dfn[maxn], low[maxn]; 10 int n, m, num; 11 12 inline int read() { 13 int x = 0, y = 1; 14 char ch = getchar(); 15 while(!isdigit(ch)) { 16 if(ch == '-') y = -1; 17 ch = getchar(); 18 } 19 while(isdigit(ch)) { 20 x = (x << 1) + (x << 3) + ch - '0'; 21 ch = getchar(); 22 } 23 return x * y; 24 } 25 26 inline void insert(int xx, int yy) { 27 e[++len].net = lin[xx]; 28 e[len].y = yy; 29 lin[xx] = len; 30 } 31 32 inline void tarjan(int x, int in_edge) { 33 dfn[x] = low[x] = ++num; 34 for(int i = lin[x]; i; i = e[i].net) { 35 int to = e[i].y; 36 if(!dfn[to]) { 37 tarjan(to, i); 38 low[x] = min(low[x], low[to]); 39 if(low[to] > dfn[x]) 40 bridge[i] = bridge[i ^ 1] = true; 41 } 42 else if(i != (in_edge ^ 1)) 43 low[x] = min(low[x], dfn[to]); 44 } 45 } 46 47 int main() { 48 n = read(), m = read(); 49 len = 1; 50 for(int i = 1; i <= m; ++i) { 51 int x, y, z; 52 x = read(), y = read(); 53 insert(x, y); 54 insert(y, x); 55 } 56 for(int i = 1; i <= n; ++i) 57 if(!dfn[i]) tarjan(i, 0); 58 for(int i = 2; i < len; i += 2) 59 if(bridge[i]) 60 cout << e[i ^ 1].y << ' ' << e[i].y << '\n'; 61 return 0; 62 }
割点的判定法则
割点的判定法则
若x不是搜索树的根节点,则x是割点当且仅当搜索树上存在x的一个子节点y,满足:
dfn[x] <= low[y]
特别地,若x是搜索树的根节点,则x是割点当且仅当搜索树上存在至少两个子节点y1, y2满足上述条件
割点判定的符号为小于等于号,不必再考虑父节点和重边的问题

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn = 100086; 4 struct node { 5 int y, net; 6 }e[maxn << 1]; 7 int lin[maxn], len = 0; 8 int n, m, root, num = 0; 9 int dfn[maxn], low[maxn]; 10 bool cut[maxn]; 11 12 inline int read() { 13 int x = 0, y = 1; 14 char ch = getchar(); 15 while(!isdigit(ch)) { 16 if(ch == '-') y = -1; 17 ch = getchar(); 18 } 19 while(isdigit(ch)) { 20 x = (x << 1) + (x << 3) + ch - '0'; 21 ch = getchar(); 22 } 23 return x * y; 24 } 25 26 inline void insert(int xx, int yy) { 27 e[++len].y = yy; 28 e[len].net = lin[xx]; 29 lin[xx] = len; 30 } 31 32 void tarjan(int x) { 33 dfn[x] = low[x] = ++num; 34 int flag = 0; 35 for(int i = lin[x]; i; i = e[i].net) { 36 int to = e[i].y; 37 if(!dfn[to]) { 38 tarjan(to); 39 low[x] = min(low[x], low[to]); 40 if(low[to] >= dfn[x]) { 41 flag++; 42 if(x != root || flag > 1) cut[x] = true; 43 } 44 } 45 else low[x] = min(low[x], dfn[to]); 46 } 47 } 48 49 int main() { 50 n = read(), m = read(); 51 len = 1; 52 for(int i = 1; i <= m; ++i) { 53 int x, y; 54 x = read(), y = read(); 55 if(x == y) continue; 56 insert(x, y); 57 insert(y, x); 58 } 59 for(int i = 1; i <= n; ++i) 60 if(!dfn[i]) { 61 root = i; 62 tarjan(i); 63 } 64 for(int i = 1; i <= n; ++i) 65 if(cut[i]) 66 cout << i << ' '; 67 cout << "are cut-vertexes" << '\n'; 68 return 0; 69 }
双连通分量
若一张无向图不存在割点,则称它为点双联通图。
无向图的“极大点双连通子图”称为“点双连通分量”,简记为“v-BCC”。无向连通图的极大边双连通图的极大边双连通子图,称为“边双连通分量”,简记为“e-DCC”
统称为“双连通分量”,简记为“BCC”
定理:
一张无向连通图是“点双连通图”,当且仅当满足下列两个条件之一:
1.图的顶点不超过2
2.图中任意两点都同时包含在至少一个简单环中。其中,简单环指的是不自交的环。
一张无向连通图是“边双连通图”,当且仅当任意一条边都包含在至少一个简单环中。
边双连通分量的求法
求出无向图中所有的桥,将桥删除后,图会分成若干块,每一个连通块都是一个“边双连通分量”
先用tarjan算法标记出所有的桥。然后再对整个无向图执行一次深度优先遍历(遍历的过程中不访问),划分出每个连通块。
边双连通分量缩点
把每个e-BCC看作一个节点,把桥边(x, y)看做连接编号为c[x]和c[y]的e-BCC对应节点的无向边,会产生一棵树(若原来的无向图不连通,则产生森林)。
这种把e-BCC收缩为一个节点的方法称为“缩点”。
把e-BCC缩点,存储在另一个邻接表中

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn = 100086; 4 struct shiki { 5 int y, net; 6 }e[maxn << 1], e_BCC[maxn << 1]; 7 int n, m, num = 0; 8 int lin[maxn], len = 0; 9 int dfn[maxn], low[maxn]; 10 bool bridge[maxn << 1]; 11 int c_id[maxn], v_bcc = 0; 12 int c_lin[maxn], c_len = 0; 13 14 inline int read() { 15 int x = 0, y = 1; 16 char ch = getchar(); 17 while(!isdigit(ch)) { 18 if(ch == '-') y = -1; 19 ch = getchar(); 20 } 21 while(isdigit(ch)) { 22 x = (x << 1) + (x << 3) + ch - '0'; 23 ch = getchar(); 24 } 25 return x * y; 26 } 27 28 inline void insert(int xx, int yy) { 29 e[++len].y = yy; 30 e[len].net = lin[xx]; 31 lin[xx] = len; 32 } 33 34 inline void t_bridge(int x, int in_edge) { 35 dfn[x] = low[x] = ++num; 36 for(register int i = lin[x]; i; i = e[i].net) { 37 int to = e[i].y; 38 if(!dfn[to]) { 39 t_bridge(to, i); 40 low[x] = min(low[x], low[to]); 41 if(dfn[x] < low[to]) 42 bridge[i] = bridge[i ^ 1] = 1; 43 } 44 else if(i != (in_edge ^ 1)) 45 low[x] = min(low[x], dfn[to]); 46 } 47 } 48 49 void dfs(int x) { 50 c_id[x] = v_bcc; 51 for(register int i = lin[x]; i; i = e[i].net) { 52 int to = e[i].y; 53 if(c_id[to] || bridge[i]) continue; 54 dfs(to); 55 } 56 } 57 58 inline void add_c(int xx, int yy) { 59 e_BCC[++c_len].y = yy; 60 e_BCC[c_len].net = c_lin[xx]; 61 c_lin[xx] = c_len; 62 } 63 64 int main() { 65 memset(dfn, 0, sizeof(dfn)); 66 n = read(), m = read(); 67 len = 1; 68 for(register int i = 1; i <= m; ++i) { 69 int x, y; 70 x = read(), y = read(); 71 insert(x, y); 72 insert(y, x); 73 } 74 for(register int i = 1; i <= n; ++i) 75 if(!dfn[i]) t_bridge(i, 0); 76 for(register int i = 2; i < len; i += 2) 77 if(bridge[i]) cout << e[i ^ 1].y <<' ' << e[i].y << '\n'; 78 for(register int i = 1; i <= n; ++i) 79 if(!c_id[i]) { 80 ++v_bcc; 81 dfs(i); 82 } 83 for(register int i = 1; i <= n; ++i) 84 cout << i << ' ' << "belong to" << ' ' << c_id[i] << '\n'; 85 for(register int i = 2; i <= len; ++i) { 86 int x = e[i ^ 1].y, y = e[i].y; 87 if(c_id[x] == c_id[y]) continue; 88 add_c(c_id[x], c_id[y]); 89 // add_c(c_id[y], c_id[x]); 90 } 91 printf("缩点后的森林, 点数%d, 边数%d(可能有重边)\n", v_bcc, c_len / 2); 92 for(register int i = 2; i <= c_len; ++i) 93 cout << e_BCC[i ^ 1].y << ' ' << e_BCC[i].y << '\n'; 94 return 0; 95 }
点双连通分量求法
若某个节点是孤立点,则它自己构成一个v-BCC。除了孤立点外,点双连通分量的大小至少为2.根据v-DCC定义的极大性,虽然桥不属于任何e-DCC,但是割点可能属于多个v-DCC
为了求出“点双连通分量”,需要在atjan算法的过程中维护一个栈,并按照如下方式维护栈中元素:
1.当一个节点第一次被访问时,把该节点入栈
2.当割点判定法则中的条件dfn[x] <= low[y]成立时,无论x是否为根,都需要:
(1)从栈顶不断弹出节点,直至节点y被弹出
(2)刚才弹出的所有节点与节点x一起构成一个v-BCC
点双连通分量缩点
因为一个割点可能属于多个v-BCC,设图中有p个割点和t个v-BCC,我们建立一张包含p+t个节点的新图,把每个v-BCC和每个割点都作为新图中的节点,并在每个割点与包含它的所有v-BCC之间连边。
这张图就变成了一棵树或是一片森林

1 //尚缺缩点 2 #include<bits/stdc++.h> 3 #define uint unsigned int 4 using namespace std; 5 const int maxn = 100086; 6 struct shiki { 7 int y, net; 8 }e[maxn << 1], vbcc[maxn]; 9 int n, m, root, num = 0; 10 int lin[maxn], len = 0, cnt = 0; 11 int dfn[maxn], low[maxn]; 12 bool cut[maxn]; 13 int s[maxn], top = 0; 14 int new_id[maxn]; 15 int v_lin[maxn], v_len = 0; 16 vector<int> dcc[maxn]; 17 int c[maxn]; 18 19 inline int read() { 20 int x = 0, y = 1; 21 char ch = getchar(); 22 while(!isdigit(ch)) { 23 if(ch == '-') y = -1; 24 ch = getchar(); 25 } 26 while(isdigit(ch)) { 27 x = (x << 1) + (x << 3) + ch - '0'; 28 ch = getchar(); 29 } 30 return x * y; 31 } 32 33 inline void insert(int xx, int yy) { 34 e[++len].y = yy; 35 e[len].net = lin[xx]; 36 lin[xx] = len; 37 } 38 39 void t_vertexes(int x) { 40 dfn[x] = low[x] = ++num; 41 s[++top] = x; 42 if(x == root && lin[x] == 0) { 43 dcc[++cnt].push_back(x); 44 return; 45 } 46 int flag = 0; 47 for(register int i = lin[x]; i; i = e[i].net) { 48 int to = e[i].y; 49 if(!dfn[to]) { 50 t_vertexes(to); 51 low[x] = min(low[x], low[to]); 52 if(dfn[x] <= low[to]) { 53 flag++; 54 if(x != root || flag > 1) cut[x] = 1; 55 cnt++; 56 int z; 57 do { 58 z = s[top--]; 59 dcc[cnt].push_back(z); 60 }while(z != to); 61 dcc[cnt].push_back(x); 62 } 63 } 64 else low[x] = min(low[x], dfn[to]); 65 } 66 } 67 68 inline void add_c(int xx, int yy) { 69 vbcc[++v_len].y = yy; 70 vbcc[v_len].net = v_lin[xx]; 71 v_lin[xx] = v_len; 72 } 73 74 int main() { 75 n = read(), m = read(); 76 for(register uint i = 1; i <= m; ++i) { 77 int x, y; 78 x = read(), y = read(); 79 insert(x, y); 80 insert(y, x); 81 } 82 for(register uint i = 1; i <= n; ++i) 83 if(!dfn[i]) { 84 root = i; 85 t_vertexes(i); 86 } 87 for(register uint i = 1; i <= n; ++i) 88 if(cut[i]) cout << i << ' '; 89 cout << "are cut-vertexes" << '\n'; 90 for(int i = 1; i <= cnt; ++i) { 91 printf("e-DCC #%d:", i); 92 for(int j = 0; j < dcc[i].size(); ++j) 93 printf(" %d", dcc[i][j]); 94 cout << '\n'; 95 } 96 num = cnt; 97 for(register int i = 1; i <= n; ++i) 98 if(cut[i]) new_id[i] = ++num;//给割点以新的编号 99 v_len = 1; 100 for(register int i = 1; i <= cnt; ++i) 101 for(register int j = 0; j < dcc[i].size(); ++j) { 102 int x = dcc[i][j]; 103 if(cut[x]) { 104 add_c(i, new_id[x]); 105 add_c(new_id[x], i); 106 } 107 else c[x] = i;//除割点外,其它点仅属于1个v-bcc 108 } 109 printf("缩点之后的森林, 点数%d, 边数%d\n", num, v_len / 2); 110 printf("编号1~%d的为原图v-BCC, 编号>%d的原图割点\n", cnt, cnt); 111 for(register int i = 2; i < v_len; i += 2) 112 printf("%d %d\n", vbcc[i ^ 1], vbcc[i]); 113 return 0; 114 }
例题1:BLO(Bzoj1123)
对于询问的节点i,可能有两种情况
1.i不是割点
2.i是割点
若i不是割点,则将i以及与i有直接相连的边删去后,图分为了i和其他节点这个两部分
即:i被孤立出来了
此时对于不能与i联通的点的个数为n-1,即有n-1个点不能与i相互到达。
因为题目求的是有序点对,也就是说,例如(1, 2)和(2, 1),这是不同的点对。
所以若i不是割点,则答案为2*(n-1)
若i是割点,则删去i以及所有与i相连的边后,图会分成若干个连通块。
最后的答案很显然,我们应该求出这些连通块的大小,两两相乘再相加
在图的连通性问题中,我们经常要从搜索树的角度来进行分析。
设在搜索树上,节点i的子节点集合中,有t割点s1,s2,s3...st满足割点判定法则dfn[i] <= low[sk]。于是删除i关联的所有边后无向图至多分成t+2个连通块
每个连通块的节点构成情况为:
1.节点i自身单独构成一个连通块
2.有t个连通块,分别由搜索树上以sk(1 <= k <= t)为根的子树中的节点构成
3.还可能有一个连通块,由除了上述节点以外的所有点构成。
(第三点,即虽然与i相连通,但i不作为搜索树的根。因为整个图是连通的,在不删掉任何一个点是,搜索树只有一个点为根,删掉与i直接相连的边,则被分开的是i,
i的子树和i的父亲所在了连通块)
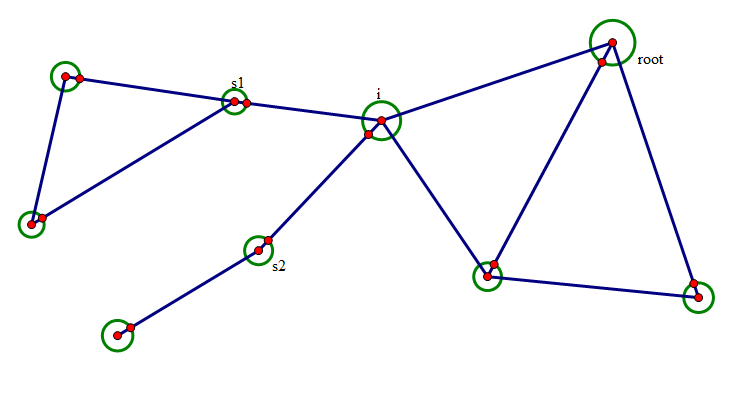
那么可以在tarjan算法执行深度优先遍历的过程正,顺便求出搜索树每棵“子树”的大小,设size[x]表示已x为根的子树的大小。
综上所述,删掉一个割点i之后,不连通的有序对数量为:
设sum = size[s1]+size[s2]+....+size[t-1]+size[t]
size[s1]*(n-size[s1])+size[s2]*(n-size[s2])+...+size[st]*(n-size[st])+1*(n-1)+(n-1-sum)*(1+sum)
1 #include<iostream> 2 #include<iomanip> 3 #include<ctime> 4 #include<cstring> 5 #include<cmath> 6 #include<cstdio> 7 #include<cstdlib> 8 #include<algorithm> 9 #include<queue> 10 #include<vector> 11 #include<map> 12 #include<stack> 13 #define ll long long 14 #define uint unsigned int 15 using namespace std; 16 const int maxn = 100010, maxm = 500010; 17 struct shiki { 18 int y, net; 19 }e[maxm << 1]; 20 int lin[maxn], len = 0; 21 int n, m, num = 0; 22 int size[maxn]; 23 ll ans[maxn]; 24 int dfn[maxn], low[maxn]; 25 bool cut[maxn]; 26 27 inline int read() { 28 int x = 0, y = 1; 29 char ch = getchar(); 30 while(!isdigit(ch)) { 31 if(ch == '-') y = -1; 32 ch = getchar(); 33 } 34 while(isdigit(ch)) { 35 x = (x << 1) + (x << 3) + ch - '0'; 36 ch = getchar(); 37 } 38 return x * y; 39 } 40 41 inline void insert(int xx, int yy) { 42 e[++len].y = yy; 43 e[len].net = lin[xx]; 44 lin[xx] = len; 45 } 46 47 void tarjan(int x) { 48 dfn[x] = low[x] = ++num, size[x] = 1; 49 int flag = 0, sum = 0; 50 for(register int i = lin[x]; i; i = e[i].net) { 51 int to = e[i].y; 52 if(!dfn[to]) { 53 tarjan(to); 54 size[x] += size[to]; 55 low[x] = min(low[x], low[to]); 56 if(dfn[x] <= low[to]) { 57 flag++; 58 ans[x] += 1ll * size[to] * (n - size[to]); 59 sum += size[to]; 60 if(x != 1 || flag > 1) cut[x] = 1; 61 } 62 } 63 else low[x] = min(low[x], dfn[to]); 64 } 65 if(cut[x]) ans[x] += 1ll * (n - sum - 1) * (sum + 1) + (n - 1); 66 else ans[x] = 2 * (n - 1); 67 } 68 69 int main() { 70 n = read(), m = read(); 71 for(register int i = 1; i <= m; ++i) { 72 int x, y; 73 x = read(), y = read(); 74 if(x == y) continue; 75 insert(x, y); 76 insert(y, x); 77 } 78 tarjan(1);//因为已经确保图是连通的 ,所以可以直接计算 79 for(register int i = 1; i <= n; ++i) 80 printf("%lld\n", ans[i]); 81 return 0; 82 }
例题2:Network(poj3694)
给定一张N个点M条边的无向连通图,然后执行Q次操作,每次想图中添加一条边,并且询问当前无向图中“桥”的数量(N <= 10^5, m <= 2*10^5, Q<=1000)
先利用tarjan算法求出无向图中所有的边双连通分量,并对所有的边双连通分量执行缩点操作。
这样就形成了一颗树,这个树上的边就是最初“桥”的个数
思考加入新的边(x, y)
对于x和y两个点
1.若两个点在同一个e-BCC中,则在x和y之间连边不会影响最终桥的数量
2.若x,y属于不同的e-BCC,则在缩点之后得到的树上,x所在的边双和y所在的边双之间的路径都不在是桥,因为将x,y连边后,他们都处在一个环中。
我们可以求出P = LCA(c_id[x], c_id[y]),即:x所在的边双与y所在的边双的最近公共祖先,同时把路径上的所有边都标记为“不是桥”。
因为数据不算大,所以我们就可以AC了
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<queue> 7 #include<cstdlib> 8 #include<ctime> 9 #include<iomanip> 10 #include<cmath> 11 using namespace std; 12 const int maxm = 500010, maxn = 100010; 13 struct shiki { 14 int y, net; 15 }e[maxm]; 16 int low[maxn], dfn[maxn], num = 0, deep[maxn]; 17 int len, n, m, lin[maxn]; 18 int flag, bridge[maxn], father[maxn]; 19 20 inline void init() { 21 len = 0, num = 0, flag = 0; 22 memset(dfn, 0, sizeof(dfn)); 23 memset(deep, 0, sizeof(deep)); 24 memset(bridge, 0, sizeof(bridge)); 25 memset(lin, 0, sizeof(lin)); 26 memset(low, 0, sizeof(low)); 27 memset(father, 0, sizeof(father)); 28 for(int i = 1; i <= n; i++) father[i] = i; 29 } 30 31 inline void insert(int xx, int yy) { 32 e[++len].y = yy; 33 e[len].net = lin[xx]; 34 lin[xx] = len; 35 } 36 37 void tarjan(int x) { 38 dfn[x] = low[x] = ++num; 39 deep[x] = deep[father[x]] + 1; 40 for(int i = lin[x]; i; i = e[i].net) { 41 int to = e[i].y; 42 if(!dfn[to]) { 43 father[to] = x; 44 tarjan(to); 45 low[x] = min(low[x], low[to]); 46 if(low[to] > dfn[x]) { 47 flag++; 48 bridge[to] = 1; 49 } 50 } 51 else if(to != father[x]) low[x] = min(low[x], dfn[to]); 52 } 53 54 } 55 56 void LCA(int u, int v) { 57 while(deep[u] > deep[v]) { 58 if(bridge[u]) flag--, bridge[u] = 0; 59 u = father[u]; 60 } 61 while(deep[v] > deep[u]) { 62 if(bridge[v]) flag--, bridge[v] = 0; 63 v = father[v]; 64 } 65 while(u != v) { 66 if(bridge[u]) flag--, bridge[u] = 0; 67 if(bridge[v]) flag--, bridge[v] = 0; 68 u = father[u]; 69 v = father[v]; 70 } 71 } 72 void ask() 73 { 74 int q, u, v; 75 scanf("%d", &q); 76 for(int i = 1; i <= q; ++i) { 77 scanf("%d%d", &u, &v); 78 LCA(u, v); 79 printf("%d\n", flag); 80 } 81 printf("\n"); 82 } 83 int main() 84 { 85 int cas = 0; 86 while(scanf("%d%d", &n, &m) != EOF) { 87 if(n == 0 && m == 0) break; 88 printf("Case %d:\n", ++cas); 89 init(); 90 int x, y; 91 while(m--) { 92 scanf("%d%d", &x, &y); 93 insert(x, y); 94 insert(y, x); 95 } 96 tarjan(1); 97 ask(); 98 } 99 return 0; 100 }



