位运算与二进制压缩

位运算

bit是度量信息的单位，包含0和1两个状态。计算机的各种运算最后无不归结为一个个bit的变化。
对于《算法竞赛进阶指南》的章节目录，是以0x00~0xFF这些由数组0~9与字母A~F表示的2位十六进制整数进行编号的，其中"0x"表示十六进制。第一章由0x00开始，前言分配序号0xFF，后记分配序号0x7F。这就是以最高二进制位为正负号位的“补码”形式表示的8位二进制数。在C++中，8位二进制数对应char类型，范围为-128~127，其中0xFF代表-1， 0x7F代表最大值127
与         或          非          异或
ans, &   or, |      not, ~       xor, ^
基本运算：
1.按位与(&)
  位运算实质是将参与运算的数字转换为二进制，而后逐位对应进行运算。
  按位与运算为：两位全为1，结果为1，即1 & 1 = 1，1 & 0 = 0，0 & 1 = 0，0 & 0 = 0。
  (1)与0相与可清零。
  (2)与1相与可保留原值，可从一个数中取某些位。例如需要取10101110中的低四位，10101110 & 00001111 = 00001110，即得到所需结果。
2.按位或(|)
   两位只要有一位为1，结果全为1。0 | 1 = 1, 1 | 0 = 1， 1 | 1 = 1， 0 | 0 = 0
   (1)与0相或可保留原值
   (2)与1相或可将对应位置变成1，例如:将x=10100000的低四位置1，使x | 00001111 = 10101111即可。
3.异或(^)
   两位不同为1,相同则为0。0 ^ 1 = 0, 1 ^ 0 = 0, 1 ^ 1 = 1, 0 ^ 0 = 0
   (1)使指定位翻转:找一个数,对应X要翻转的各位为1,其余为0,使其与x进行异或运算即可。例如:x=10101110,使最低四位翻转,x ^ 00001111 = 10100001。
   (2)交换两变量的值(比借助容器法、加减法效率高),原理:一个数对同一个数连续两次进行异或运算,结果与这个数相等(非常显然的)。交换方法:a = a ^ b，b = a ^ b，a = a ^ b。
4.非(取反(~))
   将一个数按位取反,即~0 = 1,~1 = 0。
这些符号不局限于逻辑运算，均可作用于二进制整数。为了避免混淆，统一用单词xor表示异或，而用^表示乘方
在m为二进制数中，为方便起见，通常称最低位为第0位，从右到左一次类推，最高位位m-1位。因此默认使用这种表示方式来指明二进制数以及整数在二进制表示下的位数
补码:
32位无符号整数unsigned int:
直接把这32位编码c看做32位二进制数N
32位有符号整数int:
以最高位为符号位，0表示非负数，1表示负数。
对于最高位为0的每种编码C,直接看做32位二进制数S
同时，定义该编码按位取反后得到的编码~C表示-1-S

 

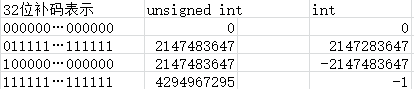
可以发现补码下每个数值都有唯一的表示方式，并且任意两个数值做加减法运算，都等价于32位补码下做最高位不进位的二进制加减法运算。发生算术溢出时，32位无符号整数相当于自动对2^32取模。而有符号整数则会因为溢出到符号位使符号位变为1而出现负数。

 （实际上半段基本都是《算法竞赛进阶指南》笔记）

二进制压缩

 

二进制状态压缩，是指将一个长度为m的bool数组用一个m位二进制整数表示并储存的方法。利用下列位运算操作可实现原bool数组中对应下标元素的存取

取出整数n在二进制表示下第k位       (n >> k) & 1
取出整数n在二进制表示下的第0~k-1位(后k位)   n & ((1 << k) - 1)
把整数n在二进制表示下的第k位取反  n xor (1 << k)
对整数n在二进制表示下的第k位赋值1  n | (1 << k)
对整数n在二进制表示下的第k位赋值为0  n & (~(1 << k))

这种方法运算简便，节省了程序运行的时间和空间。
当m不太大时，可以直接使用一个整数类型存储。当m较大时，可以使用若干个整数类型(int数组)，也可以直接使用stl中的bitset实现

例题1 :最短hamilton路径
给定一张n(n <= 20)个点的带权无向图，点从0~n-1标号，求起点0到终点n-1的最短Hamilton路径
(Hamilton路径的定义是从0到n-1不重不漏地经过每个点恰好一次)
暴力做法:枚举n个点的全排列，计算路径长度取最小值，时间复杂度为O(n * n!)，使用状态压缩DP可以优化到O(n^2 * 2^n)
在任意时刻如何表示哪些点已经被经过，哪些点没有被经过，可以使用一个n位二进制数，若其第i位为1，则表示第i个点已经被经过，反之未被经过。在任意时刻还需要知道当前处在哪一个位置
我们可以使用f[i, j](0 <= i <=2^n,  0 <= j < n)表示“点被经过的状态”对应的二进制数为i,且目前处于点j时的最短路径
在起点时，有f[1, 0] = 0,即只经过点0(i只有第0位为1)，目前处于起点0，最短路长度为0。方便起见，我们把f数组其他值设为无穷大。最终目标是f[(1 <<n) - 1, n - 1]即经过所有点(i的所有位都是1)，处于终点n-1的最短路
在任意时刻，有公式f[i, j] = min{f[i ^ (1 << j), k] + weight(k, j)}，其中0 <= k < n并且((i >>j) & 1) = 1，即当前时刻“被经过的点的状态”对应的二进制数为i,处于点j。因为j只能被恰好经过一次，所以一定是刚刚经过的，故在上一时刻“被经过的点的状态”对应的二进制数的第j位应该赋值为0，也就是i ^ (1 << j)。另外，上一时刻所处的位置可能是i ^ (1 <<j)中任意一个是1的数位k，从k走到j需要经过weight(k, j)的路程，可以考虑所有这样的k取最小值。

int f[1 << 20][20];
inline int hamilton(int n, int weight[20][20]) {
    memset(f, 0x3f, sizeof(f));
    f[1][0] = 0;
    for(int i = 1; i < 1 << n; ++i) 
        for(int j = 0; j < n; ++j) 
            if(i >> j & 1) 
                for(int k = 0; k < n; ++k)
                    if(i >> k & 1)
                        f[i][j] = min(f[i][j], f[i ^ 1 << j][k] + weight[k][j]);
    return f[(1 << n) - 1][n - 1];
}