线段树笔记(坑没填完但是已完结系列)
emmmmm….
昨天刚学完全线段树,今天先来记录一波….
指不定之后还需要写更多的东西….?
所以说目前为止只学习了基本操作和懒标记我也很无奈.jpg
线段树的基本操作
学习线段树的日常基础思考:
给定一个长度为n的数组,对其中某段序列进行m次如下可能操作:
- 给ai加上v
- 给区间[L , R]中的每一个数加上v
- 求区间[L , R]的最大/最小值
- 求区间[L , R]内所有数的和
- 查询ai的值
当然,这些操作都可以只用一个数组a进行模拟来完成
现在我们分析一下复杂度:对于操作1、5来说,每次的时间复杂度为O(1),因为只需要修改或输出数组a[i]的值就好了,但是对于操作2、3、4来说,每次的时间复杂度为O(区间长度)(时间复杂度计算我根本不会所以是搬来的现成数据)
在理论上的最坏情况下,所需要的时间复杂度为O(mn)
对于这样的复杂度,小于十万的数据或许还行,大于十万就非常棘手了
因此我们需要能够进行较大规模数据的数据结构。
例如:线段树。
线段树本质上是维护下标为1,2,..,n的n个按顺序排列的数的信息,所以,其实是“点树”,是维护n的点的信息,至于每个点的数据的含义可以有很多,
在对线段操作的线段树中,每个点代表一条线段,在用线段树维护数列信息的时候,每个点代表一个数,但本质上都是每个点代表一个数。以下,在讨论线段树的时候,区间[L,R]指的是下标从L到R的这(R-L+1)个数,而不是指一条连续的线段。只是有时候这些数代表实际上一条线段的统计结果而已。
线段树是将每个区间[L,R]分解成[L,M]和[M+1,R] (其中M=(L+R)/2 这里的除法是整数除法,即对结果下取整)直到 L==R 为止。
下面我们用一张图来演示线段树对于区间的划分过程
以长度为13的序列举例
划分过程如下
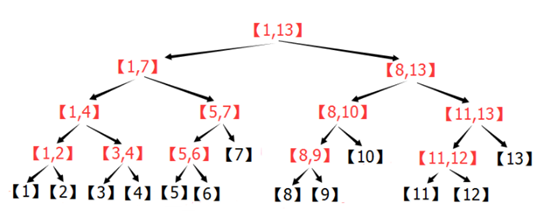
如上图,每一个节点都代表一段区间的信息
这就是区间树。可以证明,二叉区间树的深度为logn(本文中所有的log均为log2)
因为在这个树上,我们最终将这个区间都划分成了长度为1的区间
因此实际上我们要对点进行操作时或对区间进行操作时,只需要不断划分区间即可。
因为当我们在区间树上找到一个区间属于当前要操作的区间时,其从属的区间没有必要进行查找,那么显然在区间树上查询一个区间的值的时间复杂度是log级别的
这样的话我们就能将单点操作和区间操作的时间复杂度进行均摊,达到log级别。
因为线段树实际是以点来表示区间的,即:每一个点上所记录的实际是对应区间的信息
一下对与需要对二叉树的点进行说明时,用“区间”代替点
那么我们来口头实现一下最初要求实现的操作:
对单个节点进行修改,我们不断递归进行二分,知道枚举到对应的叶子节点,然后修改即可
对于区间修改来说,我们需要通过递归找到所有对应的区间(包括对应区间的子区间),然后进行修改
对于区间查询来说,只需要找到对应的区间即可
下面放一下代码?
我还是放具体题目然后丢大段代码吧…优秀板子我将放出某gy神的博客的链接…高端代码自取系列:http://www.cnblogs.com/hinanawitenshi/p/8093624.html
懒标记
我们先对代码进行一下分析:
对于操作:
单点修改只是修改树上的一条路径,长度最长为logn,因此复杂度为O(logn)
对于区间和最大(小)值查询,实际上还是对一条路径进行搜索,而且要用到的长度更小,就算极限,复杂度也只是O(logn)
但是对于区间修改,我们一次修改的是一个区间的所有点,最坏情况下,我们要对1—n所有的数都进行修改,实际是修改了整棵树,好像复杂度并没有得到改善,那么我们就得另想他法了:
仔细想想好像没有什么办法,因为要修改的话似乎必须遍历所有的数,但是实际上,我们为什么一定要进行修改呢,仔细想想,对于一个区间,我们除了在对他的左右儿子区间进行查询而进行划分时,会需要他的左右儿子区间,但是其余时刻我们好像并不需要用到,那么我们不妨只对这个区间对应的值进行修改,然后我们打上一个标记,表示如果需要划分这个区间,那么这个区间的左右儿子的值也需要修改。这个标记,我们叫做懒标记
那么这样的话我们是否达到了优化区间修改的作用呢?
对于区间修改来说,我们仅将原先要修改的子树的根节点打上了懒标记,然后返回,因此其时间复杂度与区间的询问是相同的,即O(logn)
对于区间询问来说,我们只是在遍历到带有标记的节点时,才对标记进行相关的处理,而关于标记的处理的复杂度显然是O(1)的,对整体的时间复杂度不造成影响,即区间询问的时间复杂度仍然是O(logn)
建树只是增加了标记的初始化,单点操作则不需要进行初始化,其时间复杂度不变
这样我们就将线段树一次修改的整体复杂度降到了O(logn)
#include <bits/stdc++.h> #define maxn 100057 using namespace std; struct tre{ int delta,maxx,sum; }tree[maxn]; int n,m; int a[maxn]; void pushdown(int pos,int l,int r){//懒标记下传 if(!tree[pos].delta)return; int lc=pos*2,rc=pos*2+1,m=(l+r)/1,vv=tree[pos].delta; tree[lc].sum+=(m-l+1)*vv,tree[rc].sum+=(r-m+1)*vv; tree[lc].maxx+=vv,tree[rc].maxx+=vv; tree[lc].delta+=vv,tree[rc].delta+=vv; tree[pos].delta=0; } void maintain(int pos){//重新计算区间的最大值和区间和 int lc=pos*2,rc=pos*2+1; tree[pos].maxx=max(tree[lc].maxx,tree[rc].maxx); tree[pos].sum=tree[lc].sum+tree[rc].sum; } void build(int pos,int l,int r){//建树 if(l==r){ tree[pos].delta=0; tree[pos].maxx=tree[pos].sum=a[l]; return; } int m=(l+r)/2; build(pos*2,l,m); build(pos*2+1,m+1,r); maintain(pos); } int query_max(int pos,int L,int R,int l,int r){//区间最大值查询 if(l>R||r<L) return 0; if(l>=L&&r<=R) return tree[pos].maxx; pushdown(pos,l,r); int m=l+r>>1; return max(query_max(pos<<1,L,R,l,m),query_max((pos<<1)+1,L,R,m+1,r)); } int query_sum(int pos,int L,int R,int l,int r){//区间和查询 if(l>R||r<L) return 0; if(l>=L&&r<=R) return tree[pos].sum; pushdown(pos,l,r); int m=l+r>>1; return query_sum(pos*2,L,R,l,m)+query_sum(pos*2+1,L, R,m+1,r); } void updata(int pos,int L,int R,int l,int r,int v){//区间修改 if(l>R||r<L) return; if(l>=L&&r<=R){//此大括号内容根据题意自定 tree[pos].delta+=v; tree[pos].maxx+=v; tree[pos].sum+=(r-l+1)*v; return; } pushdown(pos,l,r); int m=(l+r)/2; updata(pos*2,L,R,l,m,v); updata(pos*2+1,L,R,m+1,r,v); maintain(pos); } int main(){ cin>>n>>m; for(int i=1;i<=n;i++) cin>>a[i]; build(1,1,n); while(m--){ int bj,x,y,k; cin>>bj; if(bj==1){ cin>>x>>y>>k; updata(1,x,y,1,n,k); } else if(bj==2){ cin>>x>>y; cout<<query_sum(1,x,y,1,n)<<endl; } else{ cin>>x>>y cout<<query_max(1,x,y,1,n)<<endl; } } return 0; }
不要在意这丑陋的码风和莫名其妙的斜字体
关于区间奇数位和偶数位和的求解
对于一个区间的奇数位和偶数位,我们可以知道的是,区间总和减去奇数位和等于偶数位和
但是在维护时,区间有一些需要注意的问题
比如一个大区间
[1, 2, 3, 4, 5, 6]
二分后得到[1, 2, 3]和[4, 5, 6]
显然其中奇数位1,3,5.然而按照最初建树时情况来看,我们记录的是1, 3和4,6的值
那么如何得到5的值的,可以用右边区间的总和 减去所记录的奇数位和
由这个例子推广即可。
对于查询,我们要如何知道我们在查的是奇数位和还是偶数位和呢?
对于一个大区间[L, R]中,我们查到了一个小区间[l, r]
若l - L是奇数,我们可以知道的是,从L到l中,有算上l的三个数,所以l就是整个区间的偶数位
而l对于小区间[l, r]来说,是奇数位,所以对于小区间[l, r]我们就要取偶数位,否则就取奇数位
举例代码,20181025九校联考T2
1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 const int maxn = 500010; 5 const int maxm = 1000010; 6 const int mod = 1000000007; 7 struct shiki { 8 ll sum, delta, l; 9 }tree[maxm << 3]; 10 ll c[maxn << 1]; 11 int n, m; 12 ll fac[maxn], inv[maxn]; 13 ll ans_ma = 0, ans_mi = 0; 14 15 inline ll read() { 16 ll x = 0, y = 1; 17 char ch = getchar(); 18 while(!isdigit(ch)) { 19 if(ch == '-') y = -1; 20 ch = getchar(); 21 } 22 while(isdigit(ch)) { 23 x = (x << 1) + (x << 3) + ch - '0'; 24 ch = getchar(); 25 } 26 return x * y; 27 } 28 29 inline ll power(ll a, ll b) { 30 ll res = 1; 31 for(; b; b >>= 1) { 32 if(b & 1) res = res * a % mod; 33 a = a * a % mod; 34 } 35 return res; 36 } 37 38 inline void init() { 39 fac[1] = 1, inv[1] = 1; 40 for(int i = 2; i <= maxn; ++i) { 41 fac[i] = (fac[i - 1] * i) % mod;//阶乘 42 inv[i] = power(fac[i], mod - 2) % mod;//逆元 43 } 44 } 45 46 inline ll C(int n, int m) {//n!/m!(n-m)! = n! * m!^mod-2 * (n - m)!^mod-2 47 return fac[n] * inv[m] % mod * inv[n - m] % mod;} 48 49 inline void maintain(int pos, int l, int r) { 50 int lc = pos << 1, rc = pos << 1 | 1, mid = l + r >> 1; 51 tree[pos].sum = tree[lc].sum + tree[rc].sum; 52 tree[pos].l = tree[lc].l + (((mid - l + 1) & 1) ? tree[rc].sum - tree[rc].l : tree[rc].l); 53 tree[pos].sum %= mod, tree[pos].l %= mod; 54 } 55 56 inline void pushdown(int pos, int l, int r) { 57 if(!tree[pos].delta) return; 58 int lc = pos << 1, rc = pos << 1 | 1, mid = l + r >> 1, del = tree[pos].delta; 59 tree[lc].sum += (mid - l + 1) * del, tree[lc].l += (mid - l + 2) / 2 * del; 60 tree[rc].sum += (r - mid) * del, tree[rc].l += (r - mid + 1) / 2 * del; 61 tree[lc].sum %= mod, tree[lc].l %= mod; 62 tree[rc].sum %= mod, tree[rc].l %= mod; 63 tree[lc].delta += del, tree[rc].delta += del; 64 tree[pos].delta = 0; 65 } 66 67 void build(int pos, int l, int r){ 68 if(l == r) { 69 tree[pos].sum = c[l]; 70 tree[pos].l = c[l]; 71 return; 72 } 73 int mid = l + r >> 1; 74 build(pos << 1, l, mid); 75 build(pos << 1 | 1, mid + 1, r); 76 maintain(pos, l, r); 77 } 78 79 void update(int pos, int L, int R, int l, int r, int val) { 80 if(l > R || r < L) return ; 81 if(l >= L && r <= R) { 82 tree[pos].sum += (r - l + 1) * val; 83 tree[pos].delta += val; 84 tree[pos].l += (r - l + 2) / 2 * val; 85 tree[pos].l %= mod, tree[pos].sum %= mod; 86 return; 87 } 88 if(l != r) pushdown(pos, l, r); 89 int mid = l + r >> 1; 90 update(pos << 1, L, R, l, mid, val); 91 update(pos << 1 | 1, L, R, mid + 1, r, val); 92 maintain(pos, l, r); 93 } 94 95 ll query_sum(int pos, int L, int R, int l, int r) { 96 if(l > R || r < L) return 0; 97 if(l >= L && r <= R) return tree[pos].sum % mod; 98 if(l != r) pushdown(pos, l, r); 99 int mid = l + r >> 1; 100 return (query_sum(pos << 1, L, R, l, mid) + query_sum(pos << 1 | 1, L, R, mid + 1, r)) % mod; 101 } 102 103 ll query_l(int pos, int L, int R, int l, int r) { 104 if(l > R || r < L) return 0; 105 if(l >= L && r <= R) 106 return ((l - L) & 1) ? tree[pos].sum - tree[pos].l : tree[pos].l; 107 if(l != r) pushdown(pos, l, r); 108 int mid = l + r >> 1; 109 return (query_l(pos << 1, L, R, l, mid) + query_l(pos << 1 | 1, L, R, mid + 1, r)) % mod; 110 } 111 112 int main() { 113 freopen("sort.in", "r", stdin); 114 freopen("sort.out", "w", stdout); 115 init(); 116 n = read(), m = read(); 117 for(int i = 1; i <= 2 * n; ++i) c[i] = read(); 118 // sort(c + 1, c + 2 * n + 1); 119 if(n <= 5100) { 120 for(int i = 1; i <= m; ++i) { 121 ll opt = read(), l = read(), r = read(); 122 if(l > r) swap(l, r); 123 if(opt == 0) { 124 ll val = read(); 125 for(int j = l; j <= r; ++j) 126 c[j] += val; 127 } 128 else if(opt == 1) { 129 ll ln = (r - l + 1), lm = (r - l + 1) >> 1, mid = (l + r) >> 1; 130 ll op = C(ln, lm) % mod * power(lm + 1, mod - 2) % mod; 131 ans_ma = 0, ans_mi = 0; 132 for(int j = l; j <= mid; ++j) ans_ma -= c[j]; 133 for(int j = mid + 1; j <= r; ++j) ans_ma += c[j]; 134 for(int j = l; j <= r; j += 2) ans_mi -= c[j]; 135 for(int j = l + 1; j <= r; j += 2) ans_mi += c[j]; 136 printf("%lld %lld %lld\n", ans_ma, ans_mi, op); 137 } 138 } 139 return 0; 140 } 141 else { 142 n = 2 * n; 143 build(1, 1, n); 144 for(int i = 1; i <= m; ++i) { 145 ll opt = read(), l = read(), r = read(); 146 if(l > r) swap(l, r); 147 if(opt == 0) { 148 ll val = read(); 149 update(1, l, r, 1, n, val); 150 } 151 else if(opt == 1) { 152 ll ln = (r - l + 1), lm = (r - l + 1) >> 1, mid = (l + r) >> 1; 153 ll op = C(ln, lm) % mod * power(lm + 1, mod - 2) % mod; 154 ans_ma = (query_sum(1, mid + 1, r, 1, n) - query_sum(1, l, mid, 1, n) + mod) % mod; 155 ans_mi = (query_l(1, l + 1, r, 1, n) - query_l(1, l, r, 1, n) + mod) % mod; 156 printf("%lld %lld %lld\n", ans_ma, ans_mi, op); 157 } 158 } 159 } 160 return 0; 161 }

