模板

int bsearch()
{
int left=0,right=maxn,mid;
while(left+1<right)
{
mid=(left+right)/2;
if(check(mid)) right=mid;
else left=mid;
}
if(check(left)) return left;
else return right;
}

 

【例题】求(b^p ) %k 的值。 2<=p,b,k<=10^9

用朴素算法求aⁿ，时间复杂度为O(n)。能不能更快一些？

以a¹⁰为例。我们知道，求一个数的平方是很快的，因为不用循环。那么a¹⁰能不能转化为谁的平方？没问题，a¹⁰是a⁵的平方，也就是说，如果a⁵求出来了，那么接下来只需对这个结果平方就能得出结果，并且少做了4次乘法（求平方本身需要一次乘法）！

a⁵能不能用类似的方法求出来？按照刚才的思想，指数应该能被2整除。我们可以先求a⁴，然后再乘一个a就是a⁵。

很明显，a⁴是a²的平方，而a²可以直接求出来。于是我们最终只做了4次乘法。

10的二进制=1010。a^10=a^8*a^2.

总结刚才的思路，则有

aⁿ＝

时间复杂度为O(logn)。

另外，本题b^p会很大，所以，我们在求幂的过程中，要不停的取余数，遵循的一个数学原理，叫同余原理。  a*b%k=(a%k)*(b%k)%k，这样才能在计算中不会让数据溢出，避免了高精度运算。

具体例子： a^19= a^16*a^2*a^1

  19对应的二进制就是10011，最低位的1就是a^1 此低位的1对应 a^2，最高位的 1对应a^16.

以下的程序，s存储的是a的2的倍数次幂，而ans存储要求的结果。

#include <iostream>
#include <iomanip>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <ctime>
#include <algorithm>
using namespace std;
int b,p,k,len;
long long ans=1;
void work()
{
int temp=p, s=b;
while(temp!=0)
{
if (temp%2==1) ans=ans*s%k; //如果当前二进制位是1，就需要乘2的整次幂。
temp/=2;
s=s*s%k; // 将b的整次幂平方，对应二进制的更高一位的次幂。
}
}
int main()
{
cin>>b>>p>>k;
b%=k;
work();
cout<<ans;
return 0;
}

 

 

 

 

intcnt=0;                       // 逆序对个数

int a[100002], c[100002];

void worksort(intl,int  r) //r=右边界索引；归并排序！

{

       int  mid,tmp,i,j;

       if(r>l+1)

       {

              mid=(l+r)/2;  //中间边界

              worksort(l,mid-1);

              worksort(mid,r);

              tmp=l;

              for(i=l,j=mid;i<=mid-1 && j<=r;)   //l r, mid 表示下标，并不是具体的值？？

              {

                     if(a[i]>a[j])

                     {

                            c[tmp++]=a[j++];

                            cnt+=mid-i;    //排序找逆序对个数，

                     }

                     else

                            c[tmp++]=a[i++];

              }

              if(j<=r)

                     for(;j<=r;j++)        c[tmp++]=a[j];

              else

                     for(;i<=mid-1;i++)        c[tmp++]=a[i];

              for(i=l;i<=r;i++)    a[i]=c[i];

       }

       else

       {

              if (l+1==r)

                     if (a[l]>a[r])

                     {

                            swap(a[l],a[r]);

                            cnt++;

                     }

       }

}

 

 

 

 

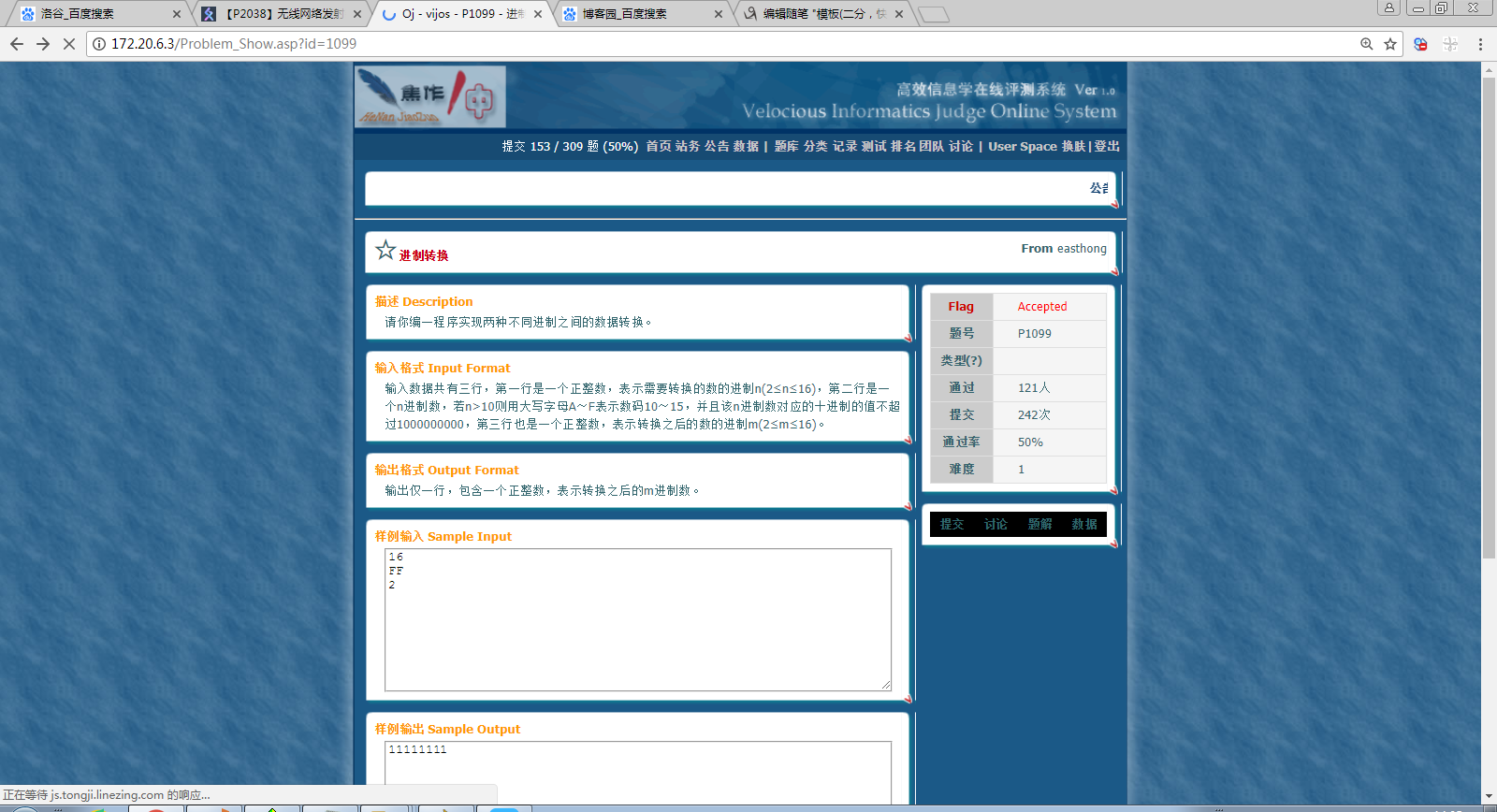
#include <iostream>
#include <cmath>
#include <cstdio>
#include <iomanip>
#include <string>
#include <cstring>
#include <algorithm>
using namespace std;
int main()
{
int a,b,s=0;
string z,c;
cin>>a;
cin>>z;
cin>>b;
for(int i=0;i<z.size();i++)
{
if(z[i]>='0'&&z[i]<='9')
s=s*a+z[i]-'0';
else
s=s*a+z[i]-'A'+10;
}
if(b==10)
cout<<s<<endl;
else
{
z.clear();
while(s>0)
{
if(s%b<10)
z=char('0'+s%b)+z;
else
z=char('A'+s%b-10)+z;
s/=b;
}
cout<<z<<endl;
}
return 0;
}

 

 

 

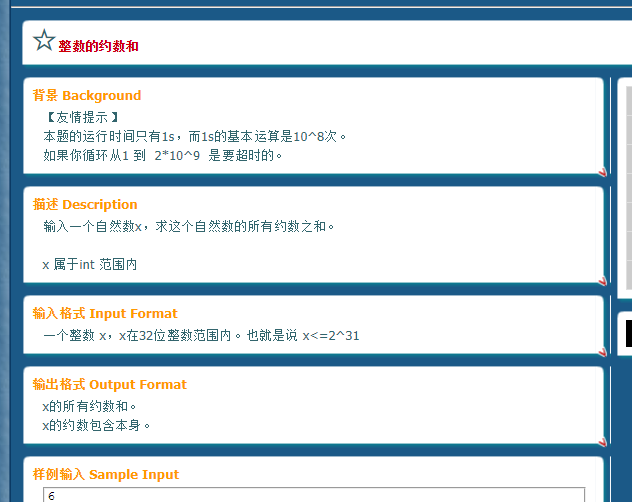
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
int n;
long long sum=0;
cin>>n;
for(int i=1;i<=sqrt(n*1.0);i++)
if(n%i==0)
{
sum+=i;
if(i!=n/i)sum+=n/i;
}
cout<<sum<<endl;
return 0;
}