【考试题解】多校A层冲刺NOIP2024模拟赛18
A. 选彩笔(rgb)
题目内容
有 \(N\) 支彩笔，每支彩笔有 \(R_i,G_i,B_i\) 三个属性。定义两只彩笔 \(i,j\) 的 Difference 值为 \(max(|R_i-R_j,G_i-G_j,B_i-B_j|)\)。定义一套彩笔的 Colorfulness 值为选中彩笔中 Difference 的最大值。求取出 \(K\) 支笔组成一套的 Colorfulness 的最小值。\(R_i,G_i,B_i\in[0,255]\)，\(K,N\in[2,10^5]\)
部分分
我不到啊。
正解
思路
观察到题面里鲜明的“最大值最小”，于是考虑二分答案。把每支笔都抽象为三维空间中的点，于是题目变为找一个正方体，包含至少 \(K\) 个点，求正方体最短边长。首先，有一个点在正方体其中一个顶点上的方案肯定不劣。于是check里枚举每一个点，分别把它作为正方体的八个顶点试一试。然后找一个正方体里有多少个点就是经典问题了。由于我们是实时询问，所以 \(O(n\log^2n)\) 的三维偏序不是很行得通。注意到至于很小，所以直接三维前缀和秒掉。复杂度 \(O(w^3+n\log w)\)。注意：如果只钦定它为三个值都取到 \(max\) 的顶点，可以过掉所有的大小样例，但是会挂在下面的数据：
输入：
2 2
1 2 2
2 1 1
输出：
1
锅了的会输出2。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,u[100001],v[100001],w[100001],col[262][262][262],pre[262][262][262];
il bool check(int x)
{
for(ri i=1;i<=a;i++)
{
ri x1=max(1,u[i]-x),y1=max(1,v[i]-x),z1=max(1,w[i]-x);
ri x2=u[i],y2=v[i],z2=w[i];
ri rn=pre[x2][y2][z2];
rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];
rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];
rn-=pre[x1-1][y1-1][z1-1];
if(rn>=b)
{
return true;
}
z1=w[i],z2=min(256,w[i]+x);
rn=pre[x2][y2][z2];
rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];
rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];
rn-=pre[x1-1][y1-1][z1-1];
if(rn>=b)
{
return true;
}
z1=max(1,w[i]-x),z2=w[i];
y1=v[i],y2=min(256,v[i]+x);
rn=pre[x2][y2][z2];
rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];
rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];
rn-=pre[x1-1][y1-1][z1-1];
if(rn>=b)
{
return true;
}
z1=w[i],z2=min(256,w[i]+x);
rn=pre[x2][y2][z2];
rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];
rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];
rn-=pre[x1-1][y1-1][z1-1];
if(rn>=b)
{
return true;
}
z1=max(1,w[i]-x),z2=w[i];
y1=max(1,v[i]-x),y2=v[i];
x1=u[i],x2=min(256,u[i]+x);
rn=pre[x2][y2][z2];
rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];
rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];
rn-=pre[x1-1][y1-1][z1-1];
if(rn>=b)
{
return true;
}
z1=w[i],z2=min(256,w[i]+x);
rn=pre[x2][y2][z2];
rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];
rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];
rn-=pre[x1-1][y1-1][z1-1];
if(rn>=b)
{
return true;
}
z1=max(1,w[i]-x),z2=w[i];
y1=v[i],y2=min(256,v[i]+x);
rn=pre[x2][y2][z2];
rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];
rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];
rn-=pre[x1-1][y1-1][z1-1];
if(rn>=b)
{
return true;
}
z1=w[i],z2=min(256,w[i]+x);
rn=pre[x2][y2][z2];
rn-=pre[x1-1][y2][z2]+pre[x2][y1-1][z2]+pre[x2][y2][z1-1];
rn+=pre[x1-1][y1-1][z2]+pre[x1-1][y2][z1-1]+pre[x2][y1-1][z1-1];
rn-=pre[x1-1][y1-1][z1-1];
if(rn>=b)
{
return true;
}
}
return false;
}
int main()
{
freopen("rgb.in","r",stdin);
freopen("rgb.out","w",stdout);
scanf("%d%d",&a,&b);
for(ri i=1;i<=a;i++)
{
scanf("%d%d%d",&u[i],&v[i],&w[i]);
u[i]++;
v[i]++;
w[i]++;
col[u[i]][v[i]][w[i]]++;
}
for(ri i=1;i<=256;i++)
{
for(ri j=1;j<=256;j++)
{
for(ri k=1;k<=256;k++)
{
ri rn=col[i][j][k];
rn+=pre[i-1][j][k]+pre[i][j-1][k]+pre[i][j][k-1];
rn-=pre[i-1][j-1][k]+pre[i-1][j][k-1]+pre[i][j-1][k-1];
rn+=pre[i-1][j-1][k-1];
pre[i][j][k]=rn;
}
}
}
ri m=0,n=255;
while(n!=m)
{
ri l=(m+n)>>1;
if(check(l))
{
n=l;
}
else
{
m=l+1;
}
}
printf("%d",m);
return 0;
}
B. 兵蚁排序(sort)
题目内容
给你两个序列 \(A,B\)，保证 \(A,B\) 中任意数出现的次数相同。构造方案把 \(A\) 转化为 \(B\)，无解输出-1。多测，\(T\) 组测试数据，\(T\le10,\sum n\le1000,A_i,B_i\in[1,n]\)。
部分分
75pts
暴搜，枚举每次的交换位置，使用哈希来进行去重+剪枝，然后跑的飞快。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,c[1001],d[1001],ans;
const int base=11491;
vector<int>vec;
deque<pair<int,int>>que;
map<pair<unsigned long long,int>,int>mp;
unsigned long long mdd;
il unsigned long long _hash(const vector<int> &x)
{
register unsigned long long rn=0;
for(ri i:x)
{
rn=rn*base+i;
}
return rn;
}
bool dfs(int x)
{
if(x>ans)
{
return false;
}
register unsigned long long re=_hash(vec);
if(re==mdd)
{
puts("0");
printf("%d\n",x-1);
while(!que.empty())
{
printf("%d %d\n",que.front().first,que.front().second);
que.pop_front();
}
return true;
}
if(mp[{re,a}]&&mp[{re,a}]<=x)
{
return false;
}
mp[{re,a}]=x;
vector<int>now(vec);
for(ri i=0;i<vec.size()-1;i++)
{
for(ri j=i+1;j<vec.size();j++)
{
sort(vec.begin()+i,vec.begin()+j+1);
que.push_back({i+1,j+1});
if(dfs(x+1))
{
return true;
}
que.pop_back();
vec=now;
}
}
return false;
}
int main()
{
freopen("sort.in","r",stdin);
freopen("sort.out","w",stdout);
scanf("%d",&a);
while(a--)
{
scanf("%d",&b);
vec.clear();
for(ri i=1;i<=b;i++)
{
scanf("%d",&c[i]);
vec.push_back(c[i]);
}
mdd=0;
for(ri i=1;i<=b;i++)
{
scanf("%d",&d[i]);
mdd=mdd*base+d[i];
}
ans=b*b;
if(!dfs(1))
{
puts("-1");
}
}
return 0;
}
正解
思路
由于题目保证 \(A,B\) 中任意数出现的次数相同，所以我们对于 \(A\) 中任意数，可以找到其对应 \(B\) 中的位置。然后根据这个东西进行冒泡排序，使映射位置靠前的往前走，如果这么走不合法，那么就是无解。具体地，如果存在位置 \(i\) 使得它后面有数权值比它大，而映射位置比它小，那么无解；否则必能通过我们的冒泡排序找到可行解。由于是冒泡排序，所以复杂度 \(O(n^2)\)。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,c[1001],d[1001],ans,to[1001];
queue<int>que[1001];
queue<pair<int,int>>ask;
il bool bubble()
{
for(ri i=1;i<b;i++)
{
for(ri j=1;j<b;j++)
{
if(to[j]>to[j+1])
{
if(c[j]<c[j+1])
{
while(!ask.empty())
{
ask.pop();
}
return false;
}
else
{
swap(c[j],c[j+1]);
swap(to[j],to[j+1]);
ask.push({j,j+1});
}
}
}
}
return true;
}
int main()
{
freopen("sort.in","r",stdin);
freopen("sort.out","w",stdout);
scanf("%d",&a);
while(a--)
{
scanf("%d",&b);
for(ri i=1;i<=b;i++)
{
scanf("%d",&c[i]);
que[c[i]].push(i);
}
for(ri i=1;i<=b;i++)
{
scanf("%d",&d[i]);
to[que[d[i]].front()]=i;
que[d[i]].pop();
}
ans=bubble();
if(ans)
{
puts("0");
printf("%d\n",ask.size());
while(!ask.empty())
{
printf("%d %d\n",ask.front().first,ask.front().second);
ask.pop();
}
}
else
{
puts("-1");
}
}
return 0;
}
C. 人口局DBA(dba)
题目内容
给你一个 \(m\) 进制数 \(n\)，长度为 \(L\) 且首位保证不为 \(0\)，求所有 \(\lt n\) 的 满足 \(S(x)=S(n)\) 的 \(m\) 进制数 \(x\) 的个数，答案对 \(10^9+7\) 取模。\(S(n)\) 为 \(n\) 在 \(m\) 进制下各位数字之和。\(m,L\in[1,2000]\)。
部分分
60pts
数位DP，但是赛时打锅了。
正解
思路
推式子。设 \(H(l,s)\) 表示长度为 \(l\) 总和为 \(s\) 的方案数。这里最困难的地方在于要保证任意数位的数要 \(\lt m\)。于是考虑容斥，发现这玩意儿推二项式反演好像很有前途，于是在 \(l,s\) 固定的情况下，设 \(F(x)\) 表示恰好有 \(i\) 个位置不满足 \(\lt m\) 条件的方案数，\(G(x)\) 表示至少有 \(i\) 个位置不满足 \(\lt m\) 条件的方案数，列出二项式反演的式子：
我们先看 \(G(x)\) 的求解。先忽略限制，插板法可得方案数为 \(\binom{s+l-1}{l-1}\)。这里可以这么理解：原来有 \(m\) 个球，现在加进去 \(n-1\) 个球，然后再随便选 \(n-1\) 个球染色，将原序列分为 \(n\) 部分。选上 \(x\) 个位置 \(\ge m\)，就先让这 \(x\) 个位置值为 \(m\)，然后剩下的数，总和为 \(s-xm\) 随便分给所有位置。方案数就是 \(\binom{s-xm+l-1}{l-1}\)。注意二项式反演的一式，我们这里 \(G(x)\) 并不是钦定的方案数，而是考虑了被选中位置的方案数。所以 \(G(x)=\binom{l}{x}\binom{s-xm+l-1}{l-1}\)。
然后反演求 \(F(x)\)。
\(H(l,s)\) 即为对应 \(l,s\) 下的 \(F(0)\) 值。
类比数位DP，设第 \(i\) 位所贡献的答案为 \(ans_i\)，则 \(ans_i=\sum\limits_{i=0}^{c[i]-1}H(l-1,s-i)\)，然后推式子：
现在重点在于简化后面的那个 \(\sum\) 项。于是充分发扬人类智慧，把这个玩意儿放杨辉三角上，发现这个东西是类似 \(C(a+b-i,b)\) 的东西，也就是杨辉三角上同一列里连续的一段区间。
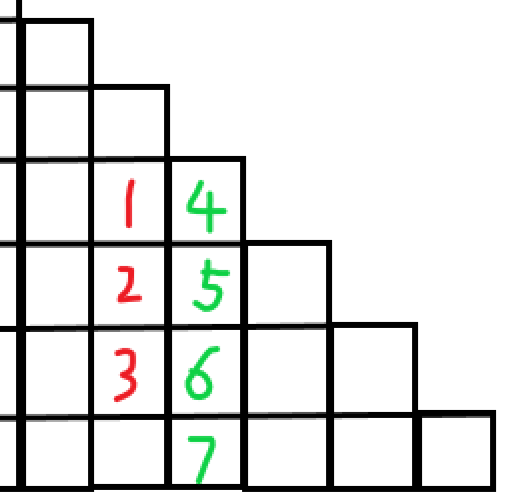
我们要求的是红色的 \(1\) 到 \(3\)，现在加进来一个 \(4\)，\(1+4=5,2+5=6,3+6=7\)，于是 \(7-4\) 就是我们想要求得答案。然后写成式子：
然后直接求就可以了。注意特判组合数为 \(0\) 的情况。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,c[2002];
const int mod=1e9+7;
long long jc[4000004],ny[4000004],sm,ans;
il long long qpow(long long x,long long y)
{
register long long rn=1;
while(y)
{
if(y&1)
{
rn=(rn*x)%mod;
}
x=(x*x)%mod;
y>>=1;
}
return rn;
}
il long long C(int x,int y)
{
if(x<y)
{
return 0;
}
return (((jc[x]*ny[x-y])%mod)*ny[y])%mod;
}
int main()
{
freopen("dba.in","r",stdin);
freopen("dba.out","w",stdout);
scanf("%d%d",&a,&b);
for(ri i=b;i>=1;i--)
{
scanf("%d",&c[i]);
sm+=c[i];
}
jc[0]=ny[0]=1;
for(ri i=1;i<=a*b;i++)
{
jc[i]=(jc[i-1]*i)%mod;
ny[i]=qpow(jc[i],mod-2);
}
for(ri i=b;i>=1;i--)
{
register long long rn=0;
for(ri j=0;j<i;j++)
{
ri op=(j&1)?-1:1;
register long long k=(C(i-1,j)*((C(sm-a*j+i-1,i-1)-C(sm-c[i]-a*j+i-1,i-1)+mod)%mod))%mod;
rn=(rn+op*k)%mod;
rn=(rn+mod)%mod;
}
ans=(ans+rn)%mod;
sm-=c[i];
}
printf("%lld",ans);
return 0;
}
D. 银行的源起(banking)
不会。
