【题解】CPS-S模拟2
Pre

赛时没有第一时间找到签到题,遂四处游走,后来决定先打T1,约1h时切了,然后1h打后3题暴力,后面推了推T4一个特殊性质,推了推T2一个特殊性质,但是T2的推假了。不太清楚怎么就来到了最后半小时,推T2的第二个特殊性质,未果,最后15min想到了T4的 \(O(n^2)\) 暴力但是没打完,算挂分吗。
T1.不相邻集合
题目内容
定义一个可重集合是不相邻集合当且仅当集合中任意两个数的差 \(\ge2\)。现在给你一个序列 \(a\),对于它的所有前缀求能组成的最大的不相邻集合的大小。
部分分
40pts
\(O(n^2)\) DP。设 \(dp[i][0]\) 表示以 \(i\) 值开头的最大不相邻集合的大小,\(dp[i][1]\) 表示以 \(i\) 值结尾的最大不相邻集合的大小,则有转移:
注意 \(+1\) 一定要放在取max外面。
10pts
在所有 \(a_i\) 都是奇数的情况下,我们任选不重复的数它们的差都一定 \(\ge2\),去重后直接统计即可。
正解
思路
对40pts的暴力进行优化。首先,重复的元素绝对没有任何贡献,所以仿照10pts的处理,先去重,也就是如果有重复的数,直接输出旧有的答案,然后不进行任何处理。
发现复杂度瓶颈在转移,有 \(O(n)\) 的遍历取max。区间最大值使我们想到线段树,于是这个东西用两颗线段树维护,支持单点赋值、区间查找最大值,复杂度 \(O(n\log n)\)。
另外还有个用并查集的做法,但是我懒得打了。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b[300003],mx,mn,num;
bool use[500005];
struct XDS
{
#define N 2200022
int left[N],right[N],num[N];
il int lft(int x)
{
return x<<1;
}
il int iht(int x)
{
return x<<1|1;
}
il void pu(int x)
{
num[x]=max(num[lft(x)],num[iht(x)]);
}
void make(int x,int lt,int rt)
{
left[x]=lt;
right[x]=rt;
if(lt==rt)
{
num[x]=0;
return;
}
ri me=(lt+rt)>>1;
make(lft(x),lt,me);
make(iht(x),me+1,rt);
pu(x);
}
void add(int x,int pl,int y)
{
if(left[x]==right[x])
{
num[x]=y;
return;
}
ri me=(left[x]+right[x])>>1;
if(pl<=me)
{
add(lft(x),pl,y);
}
else
{
add(iht(x),pl,y);
}
pu(x);
}
int found(int x,int lt,int rt)
{
if(lt>rt)
{
return 0;
}
if(lt<=left[x]&&right[x]<=rt)
{
return num[x];
}
ri me=(left[x]+right[x])>>1,rn=-inf;
if(lt<=me)
{
rn=max(rn,found(lft(x),lt,rt));
}
if(rt>me)
{
rn=max(rn,found(iht(x),lt,rt));
}
return rn;
}
#undef N
}tree[2];
int main()
{
scanf("%d",&a);
mx=-inf,mn=inf;
for(ri i=1;i<=a;i++)
{
scanf("%d",&b[i]);
mx=max(mx,b[i]);
mn=min(mn,b[i]);
}
tree[0].make(1,1,mx);
tree[1].make(1,1,mx);
for(ri i=1;i<=a;i++)
{
if(use[b[i]])
{
printf("%d ",num);
continue;
}
use[b[i]]=true;
ri j=tree[0].found(1,b[i]+2,mx);
tree[0].add(1,b[i],j+1);
num=max(num,j+1);
j=tree[1].found(1,mn,b[i]-2);
tree[1].add(1,b[i],j+1);
num=max(num,j+1);
printf("%d ",num);
}
return 0;
}
T2.线段树
题目内容
void build(int i, int l, int r) {
L[i] = l; R[i] = r;
if (l == r) return;
int mid = (l+r)/2;
build(i*2, l, mid); build(i*2+1, mid+1, r);
}
以上面的代码运行一遍build(1,1,n),求 \(\sum\limits_{i\in[x,y]}i\),答案 \(\bmod 10^9+7\)。\(1\le x\le y\le n\le 10^{18}\)。
部分分
20pts
暴力建树,统计区间和,复杂度 \(O(n\log n)\)。
正解
思路
发现复杂度主要来源于建树,考虑省略这一步,也就是 \(O(1)\) 求解某点的权值。设 \(f()\) 表示在一定条件下以某位置为根的总贡献,首先可知这个东西只和区间长度 \(n\) 和根值 \(x\) 有关,所以设为 \(f(n,x)\)(因为 \(n\) 值定了,以其为根的树的形态就定了;此时很显然它的左右儿子的值可以用根值表示,而下面的后代又可以被其左右儿子的值表示,以此类推,只要 \(n,x\) 定了,\(f()\) 的值就定了)。
然后通过理性分析||打表找规律,发现当 \(n\) 值定了以后,\(f(n,x)\) 是关于 \(x\) 的一次函数。
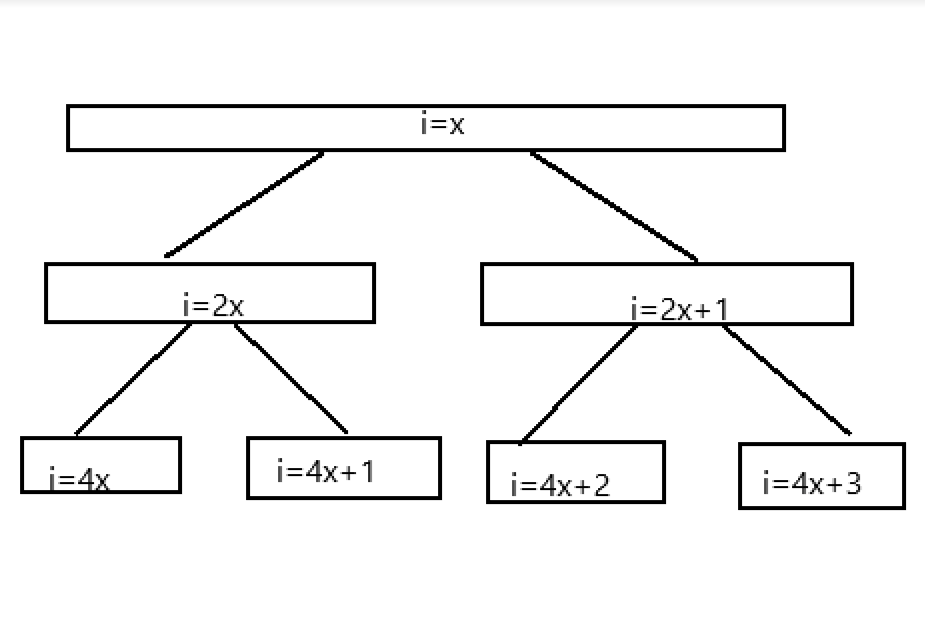
这是初始树。
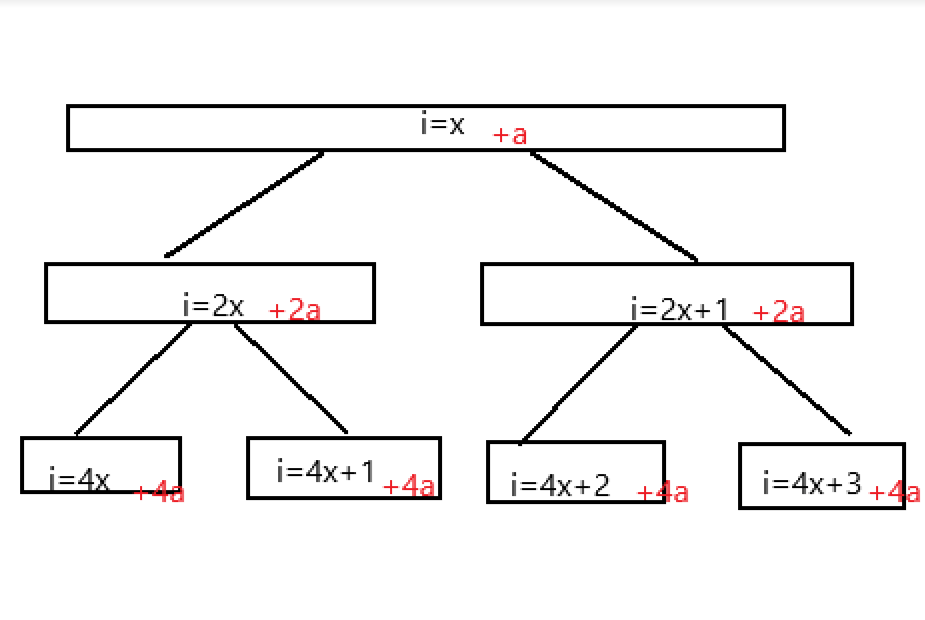
这是改变后的树。发现当根值 \(+a\),\(f(n,a)\)一定加的是 \(ka\),这时 \(f(n,x)\) 显然是一个一次函数,且这个 \(k\) 貌似只和树的形态有关系,也就是只和 \(n\) 有关系。\(x=0\) 时取到的\(b\)值同理,也只和 \(n\) 有关系。
设 \(f(n,x)=k_nx+b_n\),已知一个重要等式:
左右两边同时展开,得:
合并同类项,得:
由于是一次函数相同,所以 \(k,b\) 得分别相同,也就是:
然后就可以使用记搜 \(O(\log n)\) 的复杂度内求解线段树上一个节点的贡献了。外层还是线段树的查询,只不过不建树,递归记录区间左右端点,找到合法区间直接原地统计答案,所以再带上外层线段树的 \(\log n\),总复杂度 \(O(T\log^2n)\)。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a;
const int mod=1e9+7;
long long b,c,d;
map<long long,long long>kk,bb;
il long long K(long long x)
{
if(x==1)
{
return 1;
}
if(kk[x])
{
return kk[x];
}
kk[x]=((K(x>>1)<<1)+(K(((x+1)>>1))<<1)+1)%mod;
return kk[x];
}
il long long B(long long x)
{
if(x==1)
{
return 0;
}
if(bb[x])
{
return bb[x];
}
bb[x]=(B(x>>1)+B((x+1)>>1)+K(x>>1))%mod;
return bb[x];
}
il long long got(long long x,long long y)
{
return (K(x)*y+B(x))%mod;
}
long long found(long long x,long long lt,long long rt,long long left,long long right)
{
if(lt<=left&&right<=rt)
{
return got(right-left+1,x);
}
register long long me=(left+right)>>1,rn=0;
if(lt<=me)
{
rn+=found((x<<1)%mod,lt,rt,left,me);
rn%=mod;
}
if(rt>me)
{
rn+=found((x<<1|1)%mod,lt,rt,me+1,right);
rn%=mod;
}
return rn;
}
int main()
{
scanf("%d",&a);
while(a--)
{
scanf("%lld%lld%lld",&b,&c,&d);
printf("%lld\n",found(1,c,d,1,b));
}
return 0;
}
T3.魔法师
题目内容
有两种物品,分别是法杖与咒语,每个物品都有两个属性参数 \(a\) 和 \(b\)。发动魔法必须同时使用法杖与咒语。定义用法杖 \(p\) 与咒语 \(q\) 发动魔法的代价是 \(max(a_p+a_q,b_p+b_q)\),现在需要你支持插入一个物品与删除一个物品,并在每次操作后输出当前发动魔法的最小代价。如无法发动魔法,输出0。强制在线。
部分分
40pts
使用伟大的带修优先队列。开pair数组存物品,插入就遍历另一种物品,把所有新加的组合塞到优先队列里,删除同理,但是注意删完了这个东西要把它的两项属性赋值为-1,以后无论是插入还是删除都跳过这种物品。理论复杂度 \(O(Q^2\log Q)\),实际由于题目原因,数据造不强(其实是懒得造),复杂度吃不满,能过 \(5\times 10^4\) 的数据。
正解
思路
首先考虑如何转化掉max。为了方便描述,下面设法杖的 \(c_i=0\),咒语的 \(c_i=1\),如果 \(a_p+a_q>b_p+b_q\),那么 \(a_p-b_p>b_q-a_q\)。于是对每个物品设置一个权值 \(w_i\)。
然后充分发扬人类智慧,想到把它放线段树上维护。以 \(w_i\) 作为下标,对每个节点维护最小答案、法杖的 \(a_{min}\)、法杖的 \(b_{min}\)、咒语的 \(a_{min}\)、咒语的 \(b_{min}\),后四个合并无需多言,答案合并时,先合并左右儿子的答案,然后对于下标大小进行分讨。叶子结点使用multiset维护以方便删除。具体实现建议参考代码,复杂度 \(O(Q\log5\times10^5)\) 。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,u,v,w,ans,in;
il void pre(int &x)
{
if(b)
{
x^=ans;
}
}
struct XDS
{
#define N 1100011
#define M 500005
int left[N<<1],right[N<<1],num[N<<1],A[N][2],B[N][2];//0 a+a 1 b+b
multiset<int> msa[M][2],msb[M][2];
il int lft(int x)
{
return x<<1;
}
il int iht(int x)
{
return x<<1|1;
}
il bool leaf(int x)
{
return left[x]==right[x];
}
il void pu(int x)
{
ri na[2][2],nb[2][2];
if(leaf(lft(x)))
{
ri y=left[lft(x)];
na[0][0]=*(msa[y][0].begin());
na[0][1]=*(msa[y][1].begin());
nb[0][0]=*(msb[y][0].begin());
nb[0][1]=*(msb[y][1].begin());
}
else
{
na[0][0]=A[lft(x)][0];
na[0][1]=A[lft(x)][1];
nb[0][0]=B[lft(x)][0];
nb[0][1]=B[lft(x)][1];
}
if(leaf(iht(x)))
{
ri y=right[iht(x)];
na[1][0]=*(msa[y][0].begin());
na[1][1]=*(msa[y][1].begin());
nb[1][0]=*(msb[y][0].begin());
nb[1][1]=*(msb[y][1].begin());
}
else
{
na[1][0]=A[iht(x)][0];
na[1][1]=A[iht(x)][1];
nb[1][0]=B[iht(x)][0];
nb[1][1]=B[iht(x)][1];
}
A[x][0]=min(na[0][0],na[1][0]);
A[x][1]=min(na[0][1],na[1][1]);
B[x][0]=min(nb[0][0],nb[1][0]);
B[x][1]=min(nb[0][1],nb[1][1]);
num[x]=min(num[lft(x)],num[iht(x)]);
num[x]=min(num[x],na[0][1]+na[1][0]);
num[x]=min(num[x],nb[0][0]+nb[1][1]);
}
void make(int x,int lt,int rt)
{
left[x]=lt;
right[x]=rt;
num[x]=inf;
if(lt==rt)
{
msa[lt][0].insert(inf);
msa[lt][1].insert(inf);
msb[lt][0].insert(inf);
msb[lt][1].insert(inf);
return;
}
A[x][0]=A[x][1]=B[x][0]=B[x][1]=inf;
ri me=(lt+rt)>>1;
make(lft(x),lt,me);
make(iht(x),me+1,rt);
}
void add(int x,int pl,bool y,pair<int,int>z)
{
if(left[x]==right[x])
{
msa[pl][y].insert(z.first);
msb[pl][y].insert(z.second);
num[x]=min((*msa[pl][y].begin())+(*msa[pl][y^1].begin()),(*msb[pl][y].begin())+(*msb[pl][y^1].begin()));
return;
}
ri me=(left[x]+right[x])>>1;
if(pl<=me)
{
add(lft(x),pl,y,z);
}
else
{
add(iht(x),pl,y,z);
}
pu(x);
}
void del(int x,int pl,bool y,pair<int,int>z)
{
if(left[x]==right[x])
{
msa[pl][y].erase(msa[pl][y].find(z.first));
msb[pl][y].erase(msb[pl][y].find(z.second));
num[x]=min((*msa[pl][y].begin())+(*msa[pl][y^1].begin()),(*msb[pl][y].begin())+(*msb[pl][y^1].begin()));
return;
}
ri me=(left[x]+right[x])>>1;
if(pl<=me)
{
del(lft(x),pl,y,z);
}
else
{
del(iht(x),pl,y,z);
}
pu(x);
}
#undef N
#undef M
}tree;
int main()
{
scanf("%d%d",&a,&b);
tree.make(1,1,500001);
while(a--)
{
scanf("%d%d%d%d",&in,&u,&v,&w);
pre(v),pre(w);
if(in==1)
{
if(!u)
{
tree.add(1,v-w+250001,u,{v,w});
}
else
{
tree.add(1,w-v+250001,u,{v,w});
}
}
else
{
if(!u)
{
tree.del(1,v-w+250001,u,{v,w});
}
else
{
tree.del(1,w-v+250001,u,{v,w});
}
}
ans=tree.num[1];
if(ans>500000)
{
ans=0;
}
printf("%d\n",ans);
}
return 0;
}
T4.园艺
题目内容
你要在花园里除杂草,花园可以看作一根数轴,有 \(n\) 个位置有杂草,从左到右第 \(i\) 个位置和第 \(i+1\) 个位置间的距离是 \(D_i\)。初始时 \(n\) 个位置杂草的高度都是0,每一丛杂草每秒都会长高1。你每秒都能向左或右走一个单位长度,忽略拔掉杂草所需时间,求出你最少需要拔掉多高的杂草。
部分分
10pts
当 \(D_i=1\) 时,首先显然可能的最优解只有两种:开始选一个方向走到头再走回去。设出发点左边有 \(x\) 从草,右边有 \(y\) 丛草,则一开始向左走,所有左边的草被拔时的长度都是它到起点的距离,右边则要加上 \(2x\)。这样,我们假设先向左走更优,则有下式:
经过一番化简,会发现左右两式相等,随便选一个输出即可。
正解
思路
想到DP。首先要有一个优秀的DP设计:先设每丛杂草的贡献为当前状态下拔掉它会贡献多少长度,再设 \(dp_i\) 为在 \(i\) 处的最小总贡献。先找规律,容易发现当你向一丛杂草走去时它的贡献不变;而你远离某丛杂草一步,它的贡献会+2。那么列出状态转移方程:
这里有一个显然的结论:一个位置不会被在起点同侧&&距离更远的点转移而来。也就是说:同向下距离近的点一定比距离远的点先更新那么更新了的点会构成一个包含起点的连续区间。发现这个东西的转移会出现环,于是采用一种类似Dijkstra或是Prim的思路:双指针维护已经更新完全了的区间(备选区间),然后向左右方向更新各一个,显然取那个较小的加入备选区间更优。如果遍历备选区间转移,前缀和数组 \(S\) 维护长度,复杂度 \(O(n^2)\)。想想如何优化。
以从右向左转移为例,尝试展开状态转移方程,得:
发现其中包含乘积项,需要使用斜率优化。以 \(j\) 为 \(x\) 轴坐标,以 \(dp[j]+2aS[j]-2jS[j]\) 为 \(y\) 轴坐标加点,转移斜率为 \(-2S[i]\),求出最小答案后还要减去 \(2aS[i]\)。从左向右转移同理。复杂度 \(O(n)\)。注意double的精度问题,最好使用乘积来比较斜率,使用乘积要开__int128。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b,c[2000002];
long long pre[2000002],dp[2000002];
struct XLDDDL
{
#define N 2000002
int bg,ed;
pair<long long,long long>nm[N];
il void build(int x)
{
bg=x;
ed=bg-1;
}
il long double got(pair<long long,long long> x,pair<long long,long long> y)
{
long double rn=y.second-x.second;
rn/=(y.first-x.first);
return rn;
}
il bool check(pair<long long,long long> x,pair<long long,long long> y,pair<long long,long long> z)
{
if(got(x,y)<got(y,z))
{
return true;
}
else
{
return false;
}
}
il void push_front(pair<long long,long long> x)
{
while(bg<ed&&!check(x,nm[bg],nm[bg+1]))
{
bg++;
}
bg--;
nm[bg]=x;
}
il void push_back(pair<long long,long long> x)
{
while(bg<ed&&!check(nm[ed-1],nm[ed],x))
{
ed--;
}
ed++;
nm[ed]=x;
}
il pair<long long,long long> front(long long x)
{
while(bg<ed&&got(nm[bg],nm[bg+1])<x)
{
bg++;
}
return nm[bg];
}
il pair<long long,long long> back(long long x)
{
while(bg<ed&&got(nm[ed-1],nm[ed])>x)
{
ed--;
}
return nm[ed];
}
#undef N
}que[2];
int main()
{
scanf("%d%d",&a,&b);
que[0].build(1);
que[1].build(a);
for(ri i=2;i<=a;i++)
{
scanf("%d",&c[i]);
pre[i]=pre[i-1]+c[i];
}
memset(dp,inf,sizeof(dp));
dp[b]=0;
for(ri i=1;i<b;i++)
{
dp[b]+=pre[b]-pre[i];
}
for(ri i=b+1;i<=a;i++)
{
dp[b]+=pre[i]-pre[b];
}
ri d=a-1,lt=b,rt=b;
que[0].push_back({b,2*(a-b)*pre[b]+dp[b]});
que[1].push_front({b,-2*(b-1)*pre[b]+dp[b]});
while(d--)
{
if(lt==1||rt==a)
{
break;
}
register pair<long long,long long> qwer=que[0].front(-2*pre[lt-1]);
dp[lt-1]=qwer.second+2*pre[lt-1]*qwer.first;
dp[lt-1]-=2*a*pre[lt-1];
qwer=que[1].back(-2*pre[rt+1]);
dp[rt+1]=qwer.second+2*pre[rt+1]*qwer.first;
dp[rt+1]-=2*pre[rt+1];
if(dp[lt-1]<=dp[rt+1])
{
lt--;
que[1].push_front({lt,dp[lt]-2*(lt-1)*pre[lt]});
}
else
{
rt++;
que[0].push_back({rt,dp[rt]+2*(a-rt)*pre[rt]});
}
}
printf("%lld",min(dp[1],dp[a]));
return 0;
}
And
别再乱D造数据人了,数据真的不好造,尤其是T3这种题,原数据就难造,还需要强制在线,造数据花了我一下午。
关于T4推出来了式子又打了三天,原因是忘了斜率优化DP怎么维护凸包了。🤣👉🤡
