数据排序
排序算法基础概念
三个基本属性:时间复杂度、空间复杂度、排序算法的稳定性
排序算法的稳定性(排序后相等元素之间原有的先后顺序不变):稳定的排序算法,排序效果可以叠加。
插入排序
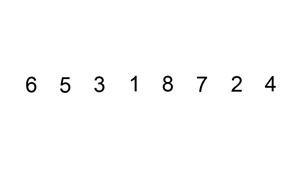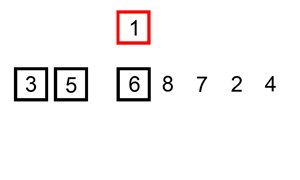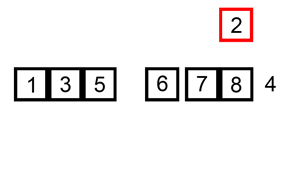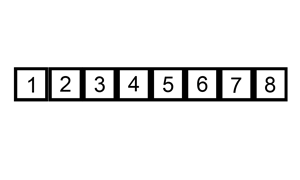
理解:取未排序区间的元素,在已排序区间找合适的插入位置进行插入
开始将数组 0 下标元素已经完成排序,数组剩余的数据循环和前面已经排序完成的数据相比较,小于比较的值就执行插入逻辑。

void InsertSort(int *A,int n){ int i,j,tmp; //双重循环,插入排序T(n)= O(n^2)。 for(i=1;i<n;i++){ tmp = A[i]; for(j=i;j>0&&A[j-1]>tmp;j--) A[j] = A[j-1]; A[j] = tmp; } }
选择排序(双重遍历)

理解:和插入排序的思想类似,不同点在于在没有排序的数组元素中进行交换找到最大或最小元素进行排序。

void SelectSort(int*a,int n){ register int i,j,min,t; for(i=0;i<n-1;i++){ min=i;//查找最小值 for(j=i+1;j<n;j++) if(a[min]>a[j]) min=j;//交换 if(min!=i){ t=a[min]; a[min]=a[i]; a[i]=t; } } }
冒泡排序(较大的元素向下沉,较小的元素向上冒泡)

理解:只循环比较相邻的数据,最大的数因为比较会下沉,较小的数会逐渐向上冒。

//冒泡排序(较大的元素向下沉,较小的元素向上冒泡) void BubbleSort(int *A,int n){ bool change; for(int i=0,change=true;i< n-1&&change;i++){ change=false; //比较相邻的两个元素,较大的元素向下沉。 for(int j=0; j<n-i-1;j++){ if(A[j] > A[j+1]){ int tmp = A[j]; A[j] = A[j+1]; A[j+1] = tmp; change = true; } } } }
希尔排序(缩小增量排序)
插入排序的更高版本,因为增量的原因一次可以消除多个逆序对。

//希尔排序(缩小增量排序),最坏情况T(n)= O(n^2) void ShellSort(int *A,int n){ int i,j,Inc,Tmp; //增量(一次消除多个逆序数) for(Inc=n/2;Inc>0;Inc/=2) for(i=Inc;i<n;i++){ Tmp = A[i]; for(j=i;j>=Inc;j-=Inc) if(Tmp<A[j-Inc]) A[j] = A[j-Inc]; else break; A[j] = Tmp; } }
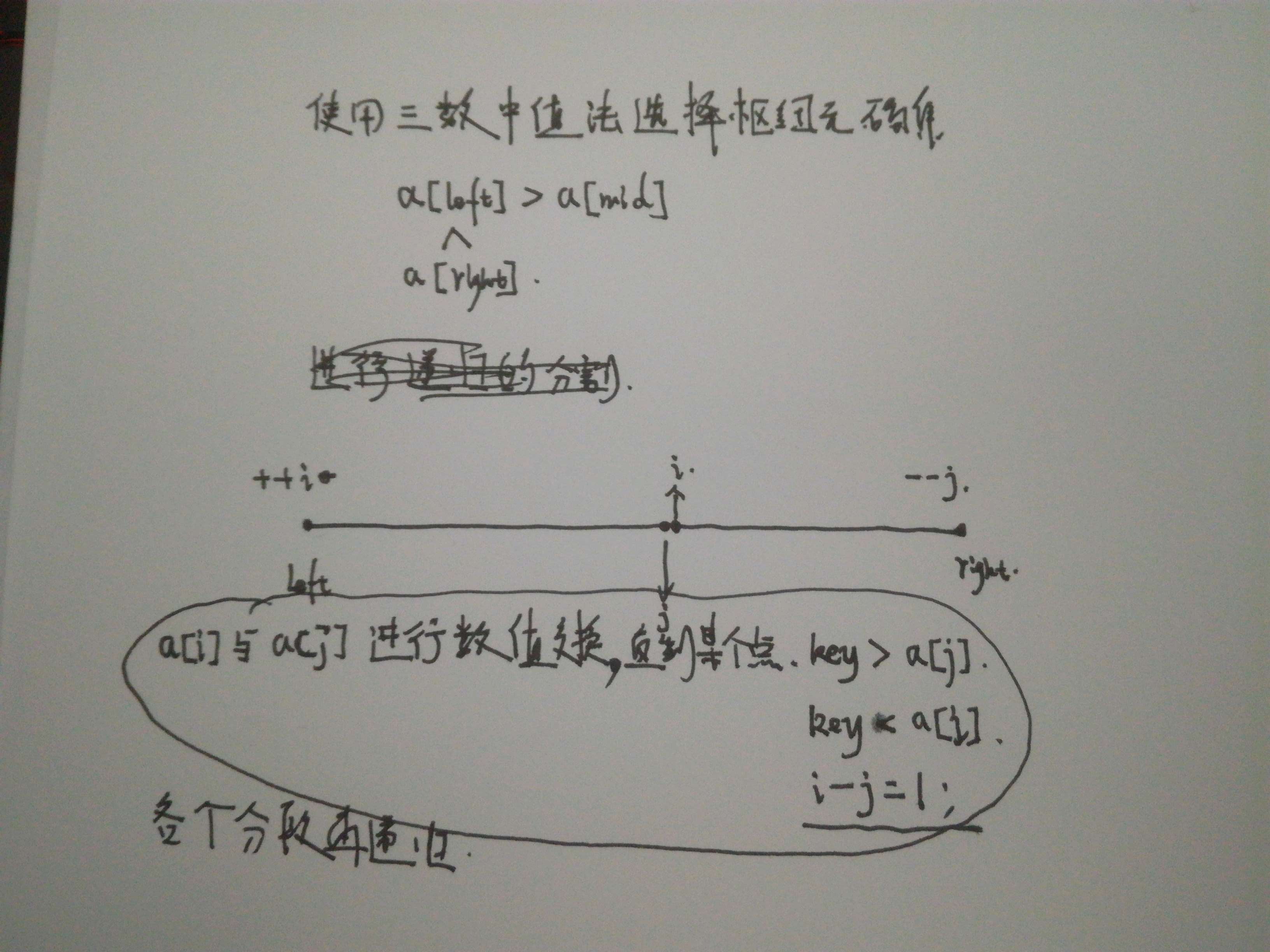
快速排序(效率=>枢纽元的选择)
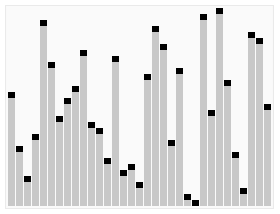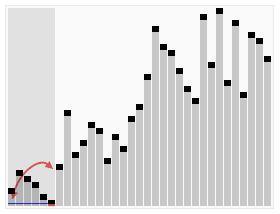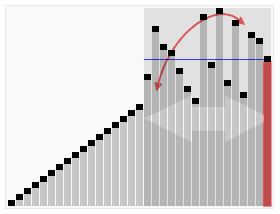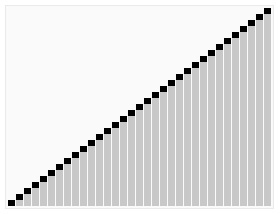
理解:图片很形象,对根据枢纽元对左右元素进行递归排序,知道退出递归。

void swap(int *a,int *b){ int temp = *a; *a = *b; *b = temp; } //三数中值分割法 void middle(int* a,int left,int right){ int mid = (left+right)/2; if(a[mid]>a[right]) swap(&a[mid],&a[right]); if(a[mid]>a[left]) swap(&a[mid],&a[left]); if(a[left]>a[right]) swap(&a[right],&a[left]); } void quick(int* a, int left, int right){ if(left >= right){ return ; } int i = left; int j = right; middle(a,left,right); int key = a[left]; while(i < j){ while(i < j && key < a[--j]); while(i < j && key > a[++i]); if(i<j) swap(&a[i],&a[j]); else break; } swap(&a[left],&a[j]); quick(a, left, i - 1); quick(a, i + 1, right); }

func QuickSort(nums []int, left int, right int) { if left >= right { //退出递归逻辑 return } randomIndex := randomPartition(nums, left, right) //对数组进行按照标准值格式化数据 QuickSort(nums, left, randomIndex-1) QuickSort(nums, randomIndex+1, right) } func randomPartition(nums []int, left int, right int) int { randomIndex := rand.Intn(right-left+1) + left //获取标准值下标 nums[right], nums[randomIndex] = nums[randomIndex], nums[right] return partition(nums, left, right) //根据标准值格式化数据 } func partition(nums []int, left int, right int) int { pivot, pivotIndex := nums[right], right for left < right { for left < right && nums[left] >= pivot { left++ } for left < right && nums[right] <= pivot { right-- } if left < right { nums[left], nums[right] = nums[right], nums[left] } } nums[pivotIndex], nums[right] = nums[right], nums[pivotIndex] return left }
归并排序(对于两个排序好的数组,归并排序)

理解:对两个排过序的数组元素进行大小比较,排列顺序。

//归并排序(数组A,数组B,合并得到的数组C,a=>A.length,b=>B.length) void MergeSort(int *A,int *B,int C[],int a,int b){ int i=0,j=0,k=0; while(true){ if(i<a&&j<b){ if(A[i]>B[j]){ C[k++] = B[j++]; }else{ C[k++] = A[i++]; } }else{ if(i<a) C[k++] = A[i++]; else if(j<b){ C[k++] = B[j++]; }else{ break; } } } }
堆排序(依次删除二叉堆的最小元素,得到序列的递增序列。要首先构建二叉堆的数据结构。)
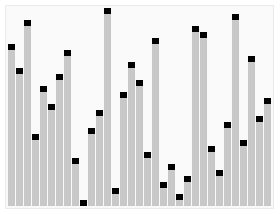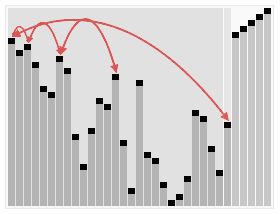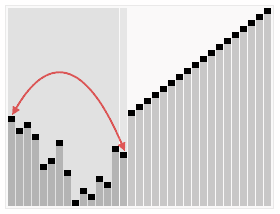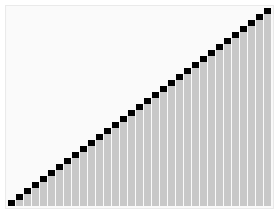

//初始化二叉堆数据结构 typedef int ElemType; //二叉堆 typedef struct Heap{ int Capacity;//容量大小 int Size;//下标 ElemType *data; }Heaps; typedef Heaps *Prity;//二叉堆指针变量 //初始化二叉堆的容量 Prity InitLize(int Max){ Prity H; H = (Heaps*)malloc(sizeof(Heaps)); if(H==NULL){ printf("Out of space"); } //初始化数组储存空间(从下标为1的元素开始存储) H->data = (ElemType*)malloc((Max+1)*sizeof(ElemType)); if(H->data==NULL){ printf("Computer out of space"); }else{ H->Capacity = Max; H->Size = 0; H->data[0] = NULL; } return H; }; //删除二叉树最小元素 ElemType DeleteMin(Prity H){ int i,child; ElemType min,last; if(!H->data[1]){ printf("Tree is NULL"); return H->data[0]; }else{ min = H->data[1]; last = H->data[H->Size--]; //i<H->size; child=>子元素 for(i=1;i*2<=H->Size;i=child){ child = i*2; if(child!=H->Size&&H->data[child+1]<H->data[child]) child++;//找到子元素较小的一个 if(last>H->data[child]) H->data[i] = H->data[child];//元素上滤,填满空的地址 else break; } H->data[i] = last;//补满、最后的元素 return min; } } //二叉堆插入元素 void Insert(ElemType X, Prity H){ int i; for(i=++H->Size;H->data[i/2]>X;i/=2) H->data[i] = H->data[i/2];//元素下移 H->data[i] = X;//元素填充 } //堆排序(依次删除二叉堆的最小元素,得到序列的递增序列) void HeapSort(int A[],int j){ int i; //初始化二叉堆 Prity Avl = InitLize(j); for(i=0;i<j;i++) Insert(A[i],Avl); //删除最小元素 for(i=0;i<j;i++){ A[i] = DeleteMin(Avl); } }




