java算法之排序算法大全
①排序
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序算法,就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范,要得到一个符合实际的优秀算法,得经过大量的推理和分析。
⓿ 复杂度
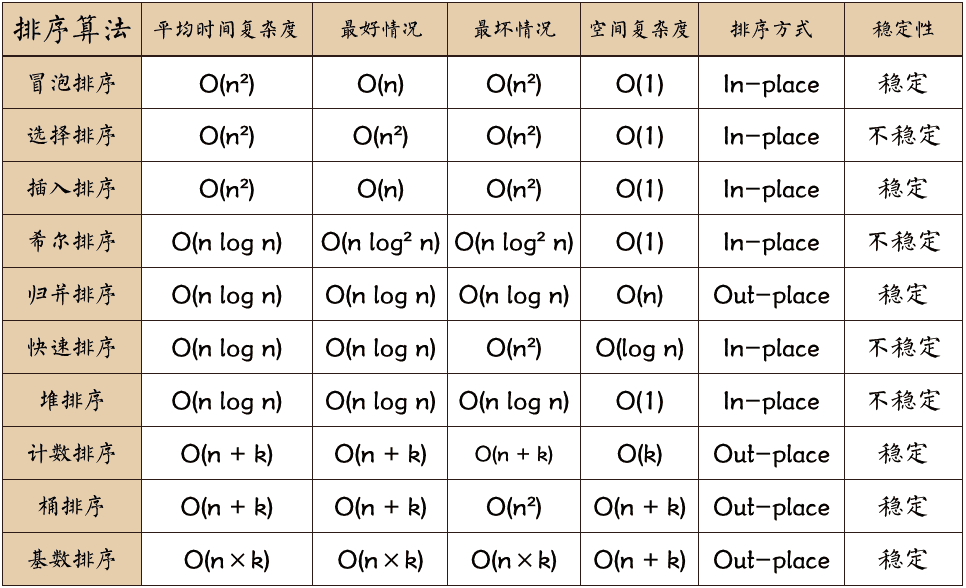
| 排序算法 | 平均时间 | 最差时间 | 稳定性 | 空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n2) | 稳定 | O(1) | n较小时好 |
| 选择排序 | O(n2) | O(n2) | 不稳定 | O(1) | n较小时好 |
| 插入排序 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已有序时好 |
| 希尔排序 | O(nlogn) | O(ns)(1<s<2) | 不稳定 | O(1) | s是所选分组 |
| 快速排序 | O(nlogn) | O(n2) | 不稳定 | O(logn) | n较大时好 |
| 归并排序 | O(nlogn) | O(nlogn) | 稳定 | O(n)/O(1) | n较大时好 |
| 基数排序 | O(n*k) | O(n*k) | 稳定 | O(n) | n为数据个数,k为数据位数 |
| 堆排序 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n较大时好 |
| 桶排序 | O(n+k) | O(n2) | 稳定 | O(n+k) | |
| 计数排序 | O(n+k) | O(n+k) | 稳定 | O(k) |
❶冒泡排序
算法步骤
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
- 一共进行了
数组元素个数-1次大循环,小循环要比较的元素越来越少。 - 优化:如果在某次大循环,发现没有发生交换,则证明已经有序。
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {4, 5, 1, 6, 2};
int[] res = bubbleSort(arr);
System.out.println(Arrays.toString(res));
}
public static int[] bubbleSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
boolean flag = true; //定义一个标识,来记录这趟大循环是否发生了交换
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = false;
}
}
//如果这次循环没发生交换,直接停止循环
if (flag){
break;
}
}
return arr;
}
}
❷选择排序
算法步骤
- 遍历整个数组,找到最小(大)的元素,放到数组的起始位置。
- 再遍历剩下的数组,找到剩下元素中的最小(大)元素,放到数组的第二个位置。
- 重复以上步骤,直到排序完成。
- 一共需要遍历
数组元素个数-1次,当找到第二大(小)的元素时,可以停止。这时最后一个元素必是最大(小)元素。
public class SelectSort {
public static void main(String[] args) {
int[] arr = {3, 1, 6, 10, 2};
int[] res = selectSort(arr);
System.out.println(Arrays.toString(res));
}
public static int[] selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if(arr[min] > arr[j]){
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
return arr;
}
}
❸插入排序
算法步骤
- 将待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
- 从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面)

黑色代表有序序列,红色代表待插入元素
public class InsertSort {
public static void main(String[] args) {
int[] arr = {3, 1, 6, 10, 2};
int[] res = insertSort(arr);
System.out.println(Arrays.toString(res));
}
public static int[] insertSort(int[] arr) {
//从数组的第二个元素开始选择合适的位置插入
for (int i = 1; i < arr.length; i++) {
//记录要插入的数据,后面移动元素可能会覆盖该位置上元素的值
int temp = arr[i];
//从已经排序的序列最右边开始比较,找到比其小的数
//变量j用于遍历前面的有序数组
int j = i;
while (j > 0 && temp < arr[j - 1]) {
//如果有序数组中的元素大于temp,则后移一个位置
arr[j] = arr[j - 1];
j--;
}
//j所指位置就是待插入的位置
if (j != i) {
arr[j] = temp;
}
}
return arr;
}
}
❹希尔排序
插入排序存在的问题
当最后一个元素为整个数组的最小元素时,需要将前面的有序数组中的每个元素都向后移一位,这样是非常花时间的。所以有了希尔排序来帮我们将数组从无序变为整体有序再变为有序。
算法步骤
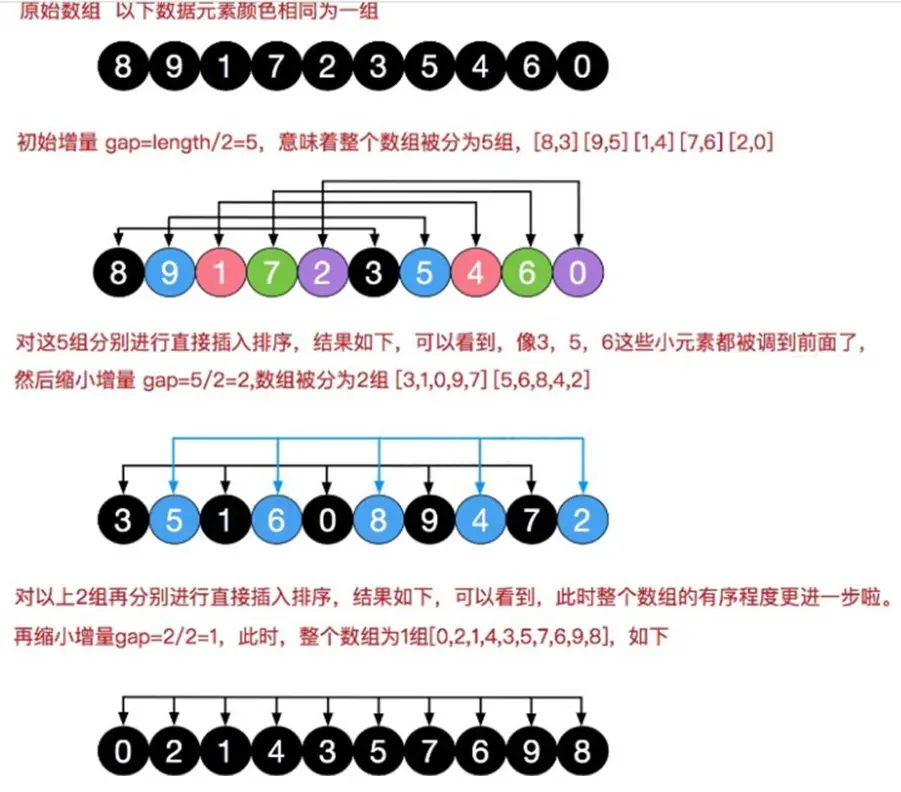
- 选择一个增量序列 t1(一般是数组长度/2),t2(一般是一个分组长度/2),……,tk,其中 ti > tj, tk = 1;
- 按增量序列个数 k,对序列进行 k 趟排序;
- 每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。当增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
public class ShellSort {
public static void main(String[] args) {
int[] arr = {3, 6, 1, 4, 5, 8, 2, 0};
int[] res = shellSort(arr);
System.out.println(Arrays.toString(res));
}
public static int[] shellSort(int[] arr) {
//将数组分为gap组,每个组内部进行插入排序
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//i用来指向未排序数组的首个元素
for (int i = gap; i < arr.length; i++) {
int temp = arr[i];
int j = i;
while (j - gap >= 0 && temp < arr[j - gap]) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
}
return arr;
}
}
❺快速排序
算法步骤
- 先把数组中的一个数当做基准数(pivot),一般会把数组中最左边的数当做基准数。
- 然后从两边进行检索。
- 先从右边检索比基准数小的
- 再从左边检索比基准数大的
- 如果检索到了,就停下,然后交换这两个元素。然后再继续检索
- 直到两边指针重合时,把基准值和重合位置值交换
- 排序好后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 然后递归地(recursive)把小于基准值的子数组和大于基准值元素的子数组再排序。
你注意最后形成的这棵二叉树是什么?是一棵二叉搜索树
你甚至可以这样理解:快速排序的过程是一个构造二叉搜索树的过程。
但谈到二叉搜索树的构造,那就不得不说二叉搜索树不平衡的极端情况,极端情况下二叉搜索树会退化成一个链表,导致操作效率大幅降低。为了避免出现这种极端情况,需要引入随机性。
public class QuickSort {
public static void main(String[] args) {
int[] arr = {8, 12, 19, -1, 45, 0, 14, 4, 11};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr, int left, int right) {
//递归终止条件
if (left >= right) return;
//定义数组第一个数为基准值
int pivot = arr[left];
//定义两个哨兵
int i = left;
int j = right;
while (i != j) {
//从右往左找比基准值小的数,找到就停止,没找到就继续左移
while (pivot <= arr[j] && i < j) j--;
//从左往右找比基准值大的数,找到就停止,没找到就继续右移
while (pivot >= arr[i] && i < j) i++;
//两边都找到就交换它们
if (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//此时,i和j相遇,把基准值和重合位置值交换
arr[left] = arr[i];
arr[i] = pivot;
quickSort(arr, left, i - 1);//对左边的子数组进行快速排序
quickSort(arr, i + 1, right);//对右边的子数组进行快速排序
}
}
private static void sort(int[] nums, int left, int right) {
if (left >= right) {
return;
}
int p = partition(nums, left, right);
sort(nums, left, p - 1);
sort(nums, p + 1, right);
}
public static int partition(int[] arr, int left, int right) {
int pivot = arr[left];//定义基准值为数组第一个数
int i = left;
int j = right;
while (i != j) {
//case1:从右往左找比基准值小的数,找到就停止,没找到就继续左移
while (pivot <= arr[j] && i < j) j--;
//case2:从左往右找比基准值大的数,找到就停止,没找到就继续右移
while (pivot >= arr[i] && i < j) i++;
//将找到的两数交换位置
if (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
arr[left] = arr[i];
arr[i] = pivot;//把基准值放到合适的位置
return i;
}
参考:快速排序法(详解)
❻归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
算法步骤
- 申请空间,该空间用来存放合并后的序列;
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
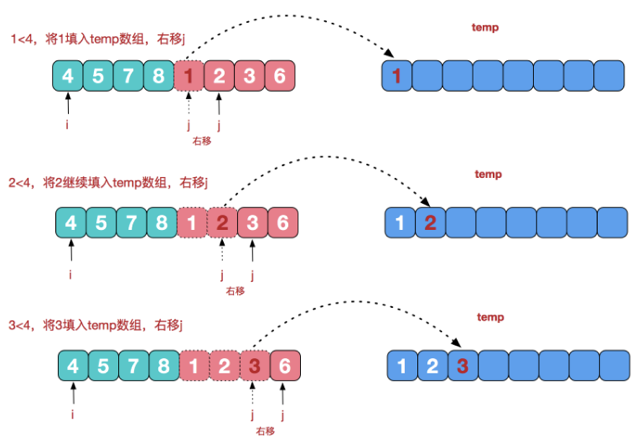
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
- 重复步骤 3 直到某一指针达到序列尾;
- 将序列剩下的所有元素直接复制到合并序列尾。
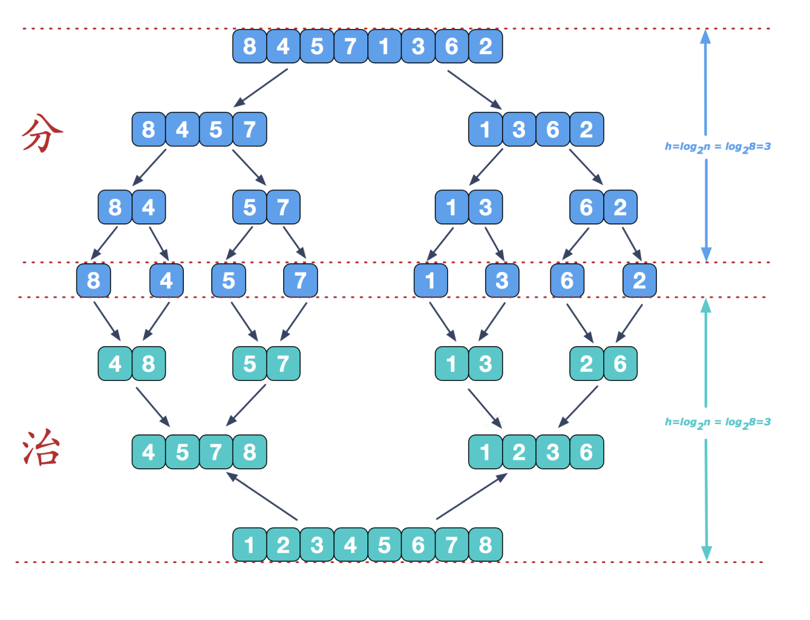
分治法
治理阶段
 |
 |
|---|---|
public class MergeSort {
public static void main(String[] args) {
int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
int[] tmp = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, tmp);
System.out.println(Arrays.toString(arr));
}
//分+治
public static void mergeSort(int[] arr, int left, int right, int[] tmp) {
if(left >= right){
return ;
}
int mid = (left + right) / 2;//中间索引
//向左递归进行分解
mergeSort(arr, left, mid, tmp);
//向右递归进行分解
mergeSort(arr, mid + 1, right, tmp);
//合并(治理)
merge(arr, left, right, tmp);
}
//治理阶段(合并)
public static void merge(int[] arr, int left, int right, int[] tmp) {
int mid = (left + right) / 2;
int i = left; // 初始化i, 左边有序序列的初始索引
int j = mid + 1; //初始化j, 右边有序序列的初始索引
int t = 0; // 指向temp数组的当前索引
//(一)
//先把左右两边(有序)的数据按照规则填充到temp数组
//直到左右两边的有序序列,有一边处理完毕为止
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
tmp[t++] = arr[i++];
} else {
tmp[t++] = arr[j++];
}
}
//(二)
//把有剩余数据的一边的数据依次全部填充到temp
while (i <= mid) {//左边的有序序列还有剩余的元素,就全部填充到temp
tmp[t++] = arr[i++];
}
while (j <= right) {
tmp[t++] = arr[j++];
}
//(三)
//将temp数组的元素拷贝到arr
t = 0;
while (left <= right) {
arr[left++] = tmp[t++];
}
}
}
❼基数排序
基数排序是使用空间换时间的经典算法
算法步骤
- 将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零
- 事先准备10个数组(10个桶),对应位数的 0-9
- 根据每个数最低位值(个位),将数放入到对应位置桶中,即进行一次排序
- 然后从 0-9 个数组/桶,依次,按照加入元素的先后顺序取出
- 以此类推,从最低位排序一直到最高位(个位->十位->百位->…->最高位),循环轮数为最大数位长度
- 排序完成以后, 数列就变成一个有序序列
- 需要我们获得最大数的位数:可以通过将最大数变为String类型,再求得它的长度即可
| 排序过程 | 排序后结果 |
|---|---|
 |
|
 |
|
 |
public class RadixSort {
public static void main(String[] args) {
int[] arr = {53, 3, 542, 748, 14, 214};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr) {
//定义一个二维数组,表示10个桶, 每个桶就是一个一维数组
int[][] bucket = new int[10][arr.length];
//为了记录每个桶中存放了多少个数据,我们定义一个数组来记录各个桶的每次放入的数据个数
//比如:bucketElementCounts[0] , 记录的就是 bucket[0] 桶的放入数据个数
int[] bucketElementCounts = new int[10];
//最大位数
int maxLen = getMaxLen(arr);
for (int i = 0, n = 1; i < maxLen; i++, n *= 10) {
//maxLen轮排序
for (int j = 0; j < arr.length; j++) {
//取出每个元素的对应位的值
int digitOfElement = arr[j] / n % 10;
//放入到对应的桶中
bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];
bucketElementCounts[digitOfElement]++;
}
//按照桶的顺序和加入元素的先后顺序取出,放入原来数组
int index = 0;
for (int k = 0; k < 10; k++) {
//如果桶中,有数据,我们才放入到原数组
int position = 0;
while (bucketElementCounts[k] > 0) {
//取出元素放入到arr
arr[index++] = bucket[k][position++];
bucketElementCounts[k]--;
}
}
}
}
//得到该数组中最大元素的位数
public static int getMaxLen(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
//将最大值转为字符串,它的长度就是它的位数
int maxLen = (max + "").length();
return maxLen;
}
}
❽堆排序
给定一个数组:String[] arr = {“S”,”O”,”R”,”T”,”E”,”X”,”A”,”M”,”P”,”L”,”E”}请对数组中的字符按从小到大排序。
实现步骤:
- 1.构造堆;
- 2.得到堆顶元素,这个值就是最大值;
- 3.交换堆顶元素和数组中的最后一个元素,此时所有元素中的最大元素已经放到合适的位置;
- 4.对堆进行调整,重新让除了最后一个元素的剩余元素中的最大值放到堆顶;
- 5.重复2~4这个步骤,直到堆中剩一个元素为止。

public class HeapSort {
public static void main(String[] args) throws Exception {
String[] arr = {"S", "O", "R", "T", "E", "X", "A", "M", "P", "L", "E"};
HeapSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
//判断heap堆中索引i处的元素是否小于索引j处的元素
private static boolean less(Comparable[] heap, int i, int j) {
return heap[i].compareTo(heap[j]) < 0;
}
//交换heap堆中i索引和j索引处的值
private static void exch(Comparable[] heap, int i, int j) {
Comparable tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}
//根据原数组source,构造出堆heap
private static void createHeap(Comparable[] source, Comparable[] heap) {
//把source中的元素拷贝到heap中,heap中的元素就形成一个无序的堆
System.arraycopy(source, 0, heap, 1, source.length);
//对堆中的元素做下沉调整(从长度的一半处开始,往索引1处扫描)
for (int i = (heap.length) / 2; i > 0; i--) {
sink(heap, i, heap.length - 1);
}
}
//对source数组中的数据从小到大排序
public static void sort(Comparable[] source) {
//构建堆
Comparable[] heap = new Comparable[source.length + 1];
createHeap(source, heap);
//定义一个变量,记录未排序的元素中最大的索引
int N = heap.length - 1;
//通过循环,交换1索引处的元素和排序的元素中最大的索引处的元素
while (N != 1) {
//交换元素
exch(heap, 1, N);
//排序交换后最大元素所在的索引,让它不要参与堆的下沉调整
N--;
//需要对索引1处的元素进行对的下沉调整
sink(heap, 1, N);
}
//把heap中的数据复制到原数组source中
System.arraycopy(heap, 1, source, 0, source.length);
}
//在heap堆中,对target处的元素做下沉,范围是0~range
private static void sink(Comparable[] heap, int target, int range) {
while (2 * target <= range) {
//1.找出当前结点的较大的子结点
int max;
if (2 * target + 1 <= range) {
if (less(heap, 2 * target, 2 * target + 1)) {
max = 2 * target + 1;
} else {
max = 2 * target;
}
} else {
max = 2 * target;
}
//2.比较当前结点的值和较大子结点的值
if (!less(heap, target, max)) {
break;
}
exch(heap, target, max);
target = max;
}
}
}
❾桶排序
❿计数排序
🌟力扣真题
215. 数组中的第K个最大元素-快选
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
方法一:暴力法
class Solution {
public int findKthLargest(int[] nums, int k) {
int len = nums.length;
Arrays.sort(nums);
return nums[len - k];
}
}
- 时间复杂度:O(NlogN),这里 N 是数组的长度,算法的性能消耗主要在排序,JDK 默认使用快速排序,因此时间复杂度为 O(NlogN);
- 空间复杂度:O(logN),这里认为编程语言使用的排序方法是「快速排序」,空间复杂度为递归调用栈的高度,为 logN。
方法二:优先队列
class Solution {
public int findKthLargest(int[] nums, int k) {
// 小顶堆,堆顶是最小元素
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int e : nums) {
// 每个元素都要过一遍二叉堆
pq.offer(e);
// 堆中元素多于 k 个时,删除堆顶元素
if (pq.size() > k) {
pq.poll();
}
}
// pq 中剩下的是 nums 中 k 个最大元素,
// 堆顶是最小的那个,即第 k 个最大元素
return pq.peek();
}
}
二叉堆插入和删除的时间复杂度和堆中的元素个数有关,在这里我们堆的大小不会超过 k,所以插入和删除元素的复杂度是 O(logk),再套一层 for 循环,假设数组元素总数为 N,总的时间复杂度就是 O(Nlogk)。空间复杂度很显然就是二叉堆的大小,为 O(k)。
- 时间复杂度:
O(Nlogk) - 空间复杂度:
O(k)
方法三:快速选择
「快速排序」虽然快,但是「快速排序」在遇到特殊测试用例(「顺序数组」或者「逆序数组」)的时候,递归树会退化成链表,时间复杂度会变成 O(N^2)。
事实上,有一个很经典的基于「快速排序」的算法,可以通过一次遍历,确定某一个元素在排序以后的位置,这个算法叫「快速选择」。
首先,题目问「第 k 个最大的元素」,相当于数组升序排序后「排名第 n - k 的元素」,为了方便表述,后文另 target = n - k。
partition 函数会将 nums[p] 排到正确的位置,使得 nums[left..p-1] < nums[p] < nums[p+1..right]:
这时候,虽然还没有把整个数组排好序,但我们已经让 nums[p] 左边的元素都比 nums[p] 小了,也就知道 nums[p] 的排名了。
那么我们可以把 p 和 target 进行比较,如果 p < target 说明第 target 大的元素在 nums[p+1..right] 中,如果 p > target 说明第 target 大的元素在 nums[left..p-1] 中。
进一步,去 nums[p+1..right] 或者 nums[left..p-1] 这两个子数组中执行 partition 函数,就可以进一步缩小排在第 target 的元素的范围,最终找到目标元素。
注意:本题必须随机初始化 pivot 元素,否则通过时间会很慢,因为测试用例中有极端测试用例。为了应对极端测试用例,使得递归树加深,可以在循环一开始的时候,随机交换第 1 个元素与任意 1 个元素的位置。
class Solution {
public int findKthLargest(int[] nums, int k) {
int len = nums.length;
int target = len - k;
int left = 0;
int right = len - 1;
return quickSelect(nums, left, right, target);
}
public static int quickSelect(int[] a, int l, int r, int k) {
if (l > r) {
return 0;
}
int p = partition(a, l, r);
if (p == k) {
return a[p];
} else {
return p < k ? quickSelect(a, p + 1, r, k) : quickSelect(a, l, p - 1, k);
}
}
static Random random = new Random();
public static int partition(int[] arr, int left, int right) {
// 生成 [left, 数组长度] 的随机数
int randomIndex = random.nextInt(right - left + 1) + left;
swap(arr, left, randomIndex);
int pivot = arr[left];//定义基准值为数组第一个数
int i = left;
int j = right;
while (i != j) {
//从右往左找比基准值小的数
while (pivot <= arr[j] && i < j) j--;
//从左往右找比基准值大的数
while (pivot >= arr[i] && i < j) i++;
if (i < j) { //如果i<j,交换它们
swap(arr, i, j);
}
}
//把基准值放到合适的位置
swap(arr, left, i);
return i;
}
public static void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
- 时间复杂度:O(N),这里 N 是数组的长度
- 空间复杂度:O(logN)
面试题 17.14. 最小K个数-快排
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
示例:
输入: arr = [1,3,5,7,2,4,6,8], k = 4
输出: [1,2,3,4]
class Solution {
public int[] smallestK(int[] arr, int k) {
int len = arr.length;
int left = 0;
int right = len - 1;
quickSelect(arr, left, right, k);
int[] res = new int[k];
for (int i = 0; i < k; ++i) {
res[i] = arr[i];
}
return res;
}
public static int quickSelect(int[] a, int l, int r, int k) {
if (l > r) {
return 0;
}
int p = partition(a, l, r);
if (p == k) {
return a[p];
} else {
return p < k ? quickSelect(a, p + 1, r, k) : quickSelect(a, l, p - 1, k);
}
}
static Random random = new Random();
public static int partition(int[] arr, int left, int right) {
// 生成 [left, 数组长度] 的随机数
int randomIndex = random.nextInt(right - left + 1) + left;
swap(arr, left, randomIndex);
int pivot = arr[left];//定义基准值为数组第一个数
int i = left;
int j = right;
while (i != j) {
//从右往左找比基准值小的数
while (pivot <= arr[j] && i < j) j--;
//从左往右找比基准值大的数
while (pivot >= arr[i] && i < j) i++;
if (i < j) { //如果i<j,交换它们
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//把基准值放到合适的位置
swap(arr, left, i);
return i;
}
public static void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
56. 合并区间-自定义排序
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
- 首先,我们将数组中的区间按照左端点升序排序。
- 然后我们将第一个区间加入结果列表res中,并按顺序依次考虑之后的每个区间:
- 如果当前区间左端点<=列表最后区间的右端点,那么它们会重合,用当前区间的右端点更新列表res中最后一个区间的右端点,将其置为二者的较大值。
- 反之,它们不会重合,直接将这个区间加入列表res的末尾;
class Solution {
public int[][] merge(int[][] intervals) {
// 按区间的 start 升序排列
//Arrays.sort(intervals, (a,b) -> a[0] - b[0]);
Arrays.sort(intervals, (a, b) -> {
return a[0] - b[0];
});
// Arrays.sort(intervals, new Comparator<int[]>() {
// public int compare(int[] a, int[] b) {
// return a[0] - b[0];
// }
// });
LinkedList<int[]> res = new LinkedList<>();
//加入第一个区间
res.add(intervals[0]);
for (int i = 1; i < intervals.length; i++) {
int[] curr = intervals[i];
// res 中最后一个元素
int[] last = res.getLast();
//当前区间左端点<=列表最后区间的右端点,那么它们会重合 [1,5] [2,4] 2<5
if (curr[0] <= last[1]) {
//用当前区间的右端点更新列表res中最后一个区间的右端点,将其置为二者的较大值。
last[1] = Math.max(last[1], curr[1]);
} else {
//反之不会重合,直接将这个区间加入列表res的末尾
res.add(curr);
}
}
return res.toArray(new int[0][0]);
}
}
快排实现
class Solution {
public int[][] merge(int[][] intervals) {
int m = intervals.length;
//先按左边界排序
sorted(intervals, 0, m - 1);
//然后逐步合并
int j = 0; //j指向要与i做对比的最后一个区间的位置
for(int i = 1; i < m; i++) { //i依次向后取
if(intervals[j][1] >= intervals[i][0]) { //两个区间有交叉
intervals[j][1] = Math.max(intervals[i][1], intervals[j][1]);
} else { //两个区间没有交叉,把i位置的向前挪,填补前面数组的空白
j++;
intervals[j] = intervals[i];
}
}
return Arrays.copyOf(intervals, j + 1);
}
private void sorted(int[][] intervals, int left, int right) {
//快速排序
if (left >= right) {
return;
}
int[] x = intervals[right];
int index = left;
for(int i = left; i < right; i++) {
if(intervals[i][0] < x[0]) {
int[] temp = intervals[index];
intervals[index] = intervals[i];
intervals[i] = temp;
index++;
}
}
intervals[right] = intervals[index];
intervals[index] = x;
sorted(intervals, left, index - 1);
sorted(intervals, index + 1, right);
}
}
147. 排序链表-插入排序
给定单个链表的头 head ,使用 插入排序 对链表进行排序,并返回 排序后链表的头 。
插入排序 算法的步骤:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时,从输入数据中删除一个元素(红色),并就地插入已排序的列表中。
对链表进行插入排序。

示例 1:
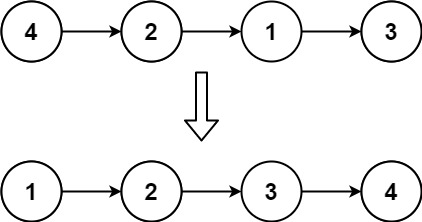
输入: head = [4,2,1,3]
输出: [1,2,3,4]
示例 2:
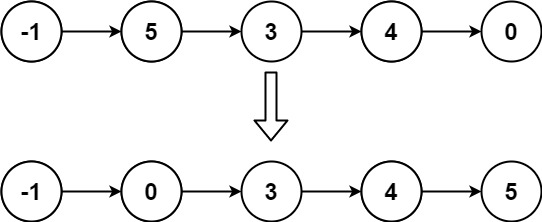
输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]
对链表进行插入排序的具体过程如下。
-
首先判断给定的链表是否为空,若为空,则不需要进行排序,直接返回。
-
创建哑节点
dummyHead,令dummyHead.next = head。引入哑节点是为了便于在head节点之前插入节点。 -
维护
lastSorted为链表的已排序部分的最后一个节点,初始时lastSorted = head。 -
维护
curr为待插入的元素,初始时curr = head.next。 -
比较
lastSorted和curr的节点值。- 若
lastSorted.val <= curr.val,说明curr应该位于lastSorted之后,将lastSorted后移一位,curr变成新的lastSorted。 - 否则,从链表的头节点开始往后遍历链表中的节点,寻找插入
curr的位置。令prev为插入curr的位置的前一个节点,进行如下操作,完成对curr的插入:
lastSorted.next = curr.next curr.next = prev.next prev.next = curr - 若
-
令
curr = lastSorted.next,此时curr为下一个待插入的元素。 -
重复第 5 步和第 6 步,直到
curr变成空,排序结束。 -
返回
dummyHead.next,为排序后的链表的头节点。
class Solution {
public ListNode insertionSortList(ListNode head) {
// 若为空,则不需要进行排序,直接返回。
if (head == null) {
return head;
}
ListNode dummyHead = new ListNode(0);
dummyHead.next = head;
ListNode lastSorted = head; // lastSorted 为链表的已排序部分的最后一个节点
ListNode curr = head.next; // curr 为待插入的元素
//从链表的第二个元素开始遍历
while (curr != null) {
if (lastSorted.val <= curr.val) { // 说明curr就应该位于lastSorted之后
lastSorted = lastSorted.next; // 直接后移一位
} else {
ListNode prev = dummyHead; //否则,从链表头结点开始向后遍历链表中的节点
while (prev.next.val <= curr.val) { // prev是插入节点curr位置的前一个节点
prev = prev.next;// 循环退出的条件是找到curr应该插入的位置
}
// 以下三行是为了完成对curr的插入
lastSorted.next = curr.next;
curr.next = prev.next;
prev.next = curr;
}
// 此时 curr 为下一个待插入的元素
curr = lastSorted.next;
}
return dummyHead.next;
}
}
148. 排序链表-归并排序
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:

输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:

输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
进阶:你可以在 O(nlog n) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
题目的进阶问题要求达到 O(nlogn) 的时间复杂度和 O(1)的空间复杂度,时间复杂度是 O(nlogn)的排序算法包括归并排序、堆排序和快速排序,快速排序的最差时间复杂度是 O(n^2),其中最适合链表的排序算法是归并排序。
归并排序基于分治算法。最容易想到的实现方式是自顶向下的递归实现,考虑到递归调用的栈空间,自顶向下归并排序的空间复杂度是 O(logn)。如果要达到O(1)的空间复杂度,则需要使用自底向上的实现方式。
对数组做归并排序的空间复杂度为 O(n),分别由新开辟数组 O(n)和递归函数调用 O(logn)组成,而根据链表特性:
- 数组额外空间:链表可以通过修改引用来更改节点顺序,无需像数组一样开辟额外空间;
- 递归额外空间:递归调用将带来O(logn)的空间复杂度,因此若希望达到 O(1)空间复杂度,则不能使用递归。
方法一:自顶向下归并排序
- 找到链表的中点,以中点为分界,将链表拆分成两个子链表。寻找链表的中点可以使用快慢指针的做法,快指针每次移动 2 步,慢指针每次移动 1 步,当快指针到达链表末尾时,慢指针指向的链表节点即为链表的中点。
- 对两个子链表分别排序。
- 将两个排序后的子链表合并,得到完整的排序后的链表。可以使用「21. 合并两个有序链表」的做法,将两个有序的子链表进行合并。
class Solution {
public ListNode sortList(ListNode head) {
return mergeSort(head);
}
// 归并排序
private ListNode mergeSort(ListNode head){
// 如果没有结点/只有一个结点,无需排序,直接返回
if (head == null || head.next == null) return head;
// 快慢指针找出中位点
ListNode fast = head.next, slow = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// 对右半部分进行归并排序
ListNode right = mergeSort(slow.next);
// 链表判断结束的标志:末尾节点.next==null
slow.next = null;
// 对左半部分进行归并排序
ListNode left = mergeSort(head);
// 合并
return mergeList(left, right);
}
// 合并两个有序链表
private ListNode mergeList(ListNode left, ListNode right){
ListNode tmpHead = new ListNode(-1); // 临时头节点
ListNode res = tmpHead; // 存放结果链表
while (left != null && right != null){
if (left.val < right.val){
res.next = left;
left = left.next;
} else {
res.next = right;
right = right.next;
}
res = res.next;
}
res.next = (left == null ? right : left);
return tmpHead.next;
}
}
复杂度分析
- 时间复杂度:O(nlogn),其中 n 是链表的长度。
- 空间复杂度:O(logn),空间复杂度主要取决于递归调用的栈空间。
方法二:自底向上归并排序
将方法1改为迭代,节省递归占用的栈空间,每轮从链表上分别取1、2、4、8。。。。长度的子链表,两两依次合并模拟递归中的自底向上
用自底向上的方法实现归并排序,则可以达到 O(1) 的空间复杂度。
- 首先求得链表的长度 length,然后将链表拆分成子链表进行合并。
- 用 subLength表示每次需要排序的子链表的长度,初始时 subLength=1。
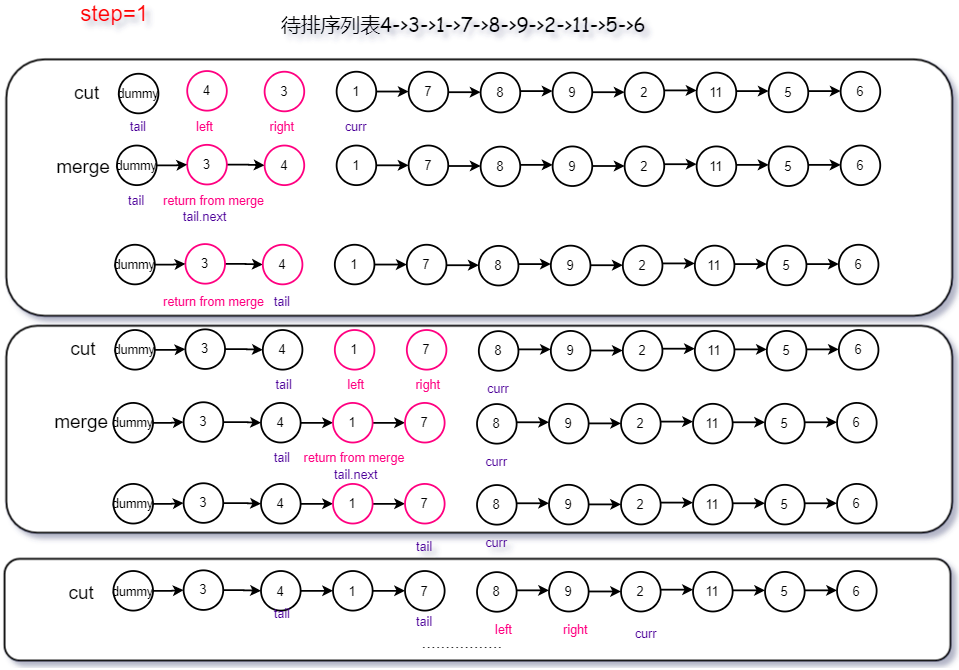
- 每次将链表拆分成若干个长度为 subLength 的子链表(最后一个子链表的长度可以小于 subLength),按照每两个子链表一组进行合并,合并后即可得到若干个长度为 subLength×2的有序子链表(最后一个子链表的长度可以小于 subLength×2)。合并两个子链表仍然使用「21. 合并两个有序链表」的做法。
- 将 subLength 的值加倍,重复第 2 步,对更长的有序子链表进行合并操作,直到有序子链表的长度大于或等于 length,整个链表排序完毕。
class Solution {
public ListNode sortList(ListNode head) {
// 如果没有结点/只有一个结点,无需排序,直接返回
if (head == null || head.next == null) return head;
// 统计链表长度
int len = 0;
ListNode curr = head;
while (curr != null) {
len++;
curr = curr.next;
}
ListNode dummy = new ListNode(-1, head);
// 外层遍历step 内层处理每step个元素进行一次merge
for (int subLength = 1; subLength < len; subLength <<= 1) {
// 用于连接合并后排序好的链表,相当于记录结果
ListNode tail = dummy;
// 记录拆分链表的位置
curr = dummy.next;
// 每次遍历整条链表,将链表拆分成若干个长度为 subLength 的子链表,然后合并。
while (curr != null) {
ListNode left = curr; // 第一个链表的头节点
// 拆分subLength长度的链表1
ListNode right = cut(left, subLength);
// 拆分subLength长度的链表2
curr = cut(right, subLength);
// 合并两个subLength长度的有序链表
tail.next = merge(left, right);
// 将tail移动到subLength × 2 的位置,以连接下一次合并的结果
while (tail.next != null) {
tail = tail.next;
}
}
}
return dummy.next;
}
// 将链表从from开始切掉前step个元素,返回后一个元素
public ListNode cut(ListNode from, int step) {
step--;
while (from != null && step > 0) {
from = from.next;
step--;
}
if (from == null) {
return null;
} else {
ListNode next = from.next;
from.next = null;
return next;
}
}
// 题21. 合并两个有序链表
private ListNode merge(ListNode left, ListNode right){
ListNode dummy = new ListNode(0);// 临时头节点
ListNode res = dummy;
while (left != null && right != null){
if (left.val < right.val){
res.next = left;
left = left.next;
} else {
res.next = right;
right = right.next;
}
res = res.next;
}
res.next = (left == null ? right : left);
return dummy.next;
}
}
方法三:快速排序
- 快排的partition操作变成了将单链表分割为<pivot和pivot以及>=pivot三个部分
- 递推对分割得到的两个单链表进行快排
- 回归时将pivot和排序后的两个单链表连接,并返回排序好的链表头尾节点
class Solution {
public ListNode sortList(ListNode head) {
if(head==null||head.next==null) return head;
// 没有条件,创造条件。自己添加头节点,最后返回时去掉即可。
ListNode newHead=new ListNode(-1);
newHead.next=head;
return quickSort(newHead,null);
}
// 带头结点的链表快速排序
private ListNode quickSort(ListNode head, ListNode end){
if (head==end||head.next==end||head.next.next==end) return head;
// 将小于划分点的值存储在临时链表中
ListNode tmpHead=new ListNode(-1);
// partition为划分点,p为链表指针,tp为临时链表指针
ListNode partition=head.next,p=partition,tp=tmpHead;
// 将小于划分点的结点放到临时链表中
while (p.next!=end){
if (p.next.val<partition.val){
tp.next=p.next;
tp=tp.next;
p.next=p.next.next;
}else {
p=p.next;
}
}
// 合并临时链表和原链表,将原链表接到临时链表后面即可
tp.next=head.next;
// 将临时链表插回原链表,注意是插回!(不做这一步在对右半部分处理时就断链了)
head.next=tmpHead.next;
quickSort(head, partition);
quickSort(partition, end);
return head.next;
}
}
75. 颜色分类-快速排序
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
利用快排parption思想
class Solution {
public void sortColors(int[] nums) {
int left = 0, right = nums.length - 1;
int i = 0;
while (i <= right) {
if (nums[i] == 0) {
swap(nums, left, i);
left++;
i++;
} else if (nums[i] == 2) {
swap(nums, i, right);
right--;
} else {
i++;
}
}
}
void swap(int[] nums, int i, int j) {
int c = nums[i];
nums[i] = nums[j];
nums[j] = c;
}
}
//冒泡
class Solution {
public void sortColors(int[] nums) {
for(int i = 0;i < nums.length - 1;i++){
for(int j = 0; j < nums.length - i - 1;j++){
if(nums[j] > nums[j+1]){
int temp = nums[j];
nums[j] = nums[j+1];
nums[j+1] = temp;
}
}
}
}
}
912. 排序数组-手撕排序
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
快排:排序数组 - 题解
class Solution {
public int[] sortArray(int[] nums) {
quickSort(nums, 0, nums.length - 1);
return nums;
}
public void quickSort(int[] nums, int left, int right){
if(left >= right) return;
int p = parption(nums, left, right);
quickSort(nums, left, p - 1);
quickSort(nums, p + 1, right);
}
Random random = new Random();
public int parption(int[] nums, int left, int right){
int r = random.nextInt(right - left + 1) + left;
swap(nums, left, r);
int pivot = nums[left];
int i = left;
int j = right;
while(i != j){
while(nums[j] >= pivot && i < j) j--;
while(nums[i] <= pivot && i < j) i++;
if(i < j){
swap(nums, i, j);
}
}
swap(nums, left, i);
return i;
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
归并排序
class Solution {
public int[] sortArray(int[] nums) {
int[] tmp = new int[nums.length];
mergeSort(nums, 0, nums.length - 1, tmp);
return nums;
}
public void mergeSort(int[] nums, int left, int right, int[] tmp){
if(left >= right){
return ;
}
int mid = left + (right - left) / 2;
mergeSort(nums, left, mid, tmp);
mergeSort(nums, mid + 1 , right, tmp);
merge(nums, left, right, tmp);
}
public void merge(int[] nums, int left, int right, int[] tmp){
int mid = left + (right - left) / 2;
int i = left;
int j = mid + 1;
int t = 0;
while(i <= mid && j <= right){
if(nums[i] <= nums[j]){
tmp[t++] = nums[i++];
} else {
tmp[t++] = nums[j++];
}
}
while(i <= mid){
tmp[t++] = nums[i++];
}
while(j <= right){
tmp[t++] = nums[j++];
}
t = 0;
while(left <= right){
nums[left++] = tmp[t++];
}
}
}
406. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
一般这种数对,还涉及排序的,根据第一个元素正向排序,根据第二个元素反向排序,或者根据第一个元素反向排序,根据第二个元素正向排序,往往能够简化解题过程。
class Solution {
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people, new Comparator<int[]>(){
@Override
public int compare(int[] a, int[] b){
if(a[0] != b[0]){
//第一个元素不相等时,第一个元素降序
return b[0] - a[0];
} else {
//第一个元素相等时,第二个元素升序
return a[1] - b[1];
}
}
});
List<int[]> list = new ArrayList<>();
for(int i = 0; i < people.length; i++){
if (list.size() > people[i][1]){
//结果集中元素个数大于第i个人前面应有的人数时,将第i个人插入到结果集的 people[i][1]位置
list.add(people[i][1],people[i]);
}else{
//结果集中元素个数小于等于第i个人前面应有的人数时,将第i个人追加到结果集的后面
list.add(people[i]);
}
}
//将list转化为数组,然后返回
return list.toArray(new int[list.size()][]);
}
}
581. 最短无序连续子数组
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组,并输出它的长度。
示例 1:
输入:nums = [2,6,4,8,10,9,15]
输出:5
解释:你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。
示例 2:
输入:nums = [1,2,3,4]
输出:0
示例 3:
输入:nums = [1]
输出:0
排序
将给定的数组 nums 表示为三段子数组拼接的形式,记作 numsA,numsB,numsC。本题要求找到最短的 numsB。
因此我们将原数组 nums 排序与原数组进行比较,取最长的相同的前缀为 numsA,取最长的相同的后缀为 numsC,这样我们就可以取到最短的 numsB。
创建数组 nums 的拷贝,记作数组 numsSorted,并对该数组进行排序,然后我们从左向右找到第一个两数组不同的位置,即为 numsB 的左边界。同理也可以找到 numsB 右边界。最后我们输出 numsB 的长度即可。
特别地,当原数组有序时,numsB 的长度为 000,我们可以直接返回结果。
//时间复杂度:O(nlogn),空间复杂度:O(n)
class Solution {
public int findUnsortedSubarray(int[] nums) {
if(isSorted(nums)){
return 0;
}
int n = nums.length;
int[] numSorted = new int[n];
System.arraycopy(nums, 0, numSorted, 0, n);
Arrays.sort(numSorted);
int left = 0; //最长相同前缀
while(nums[left] == numSorted[left]){
left++;
}
int right = n - 1; //最长相同后缀
while(nums[right] == numSorted[right]){
right--;
}
return right - left + 1;
}
public boolean isSorted(int[] nums) {
for (int i = 1; i < nums.length; i++) {
if (nums[i] < nums[i - 1]) {
return false;
}
}
return true;
}
}
一次遍历
如何确定nums[B]的范围[left,right]?
- numsB 是无序的,numsB 中最小元素左侧可能有比其大的,最大元素右侧可能有比其小的;
- 初始最大元素max为Integer.MIN_VALUE,正序遍历数组,如果当前元素比最大元素大,更新max; 如果当前元素比最大元素小,就说明其是numsB的一部分,动态维护numsB右边界right;
- 初始最小元素min为Integer.MAX_VALUE,倒序遍历数组,如果当前元素比最小元素小,更新min; 如果当前元素比最小元素大,就说明其是numsB的一部分,动态维护numsB左边界left;
- 返回最短长度right-left+1;
- 由于初始时left=-1,right=-1,如果整体有序,right和left保持-1,对于有序数组需要单独判断,返回0;
class Solution {
public int findUnsortedSubarray(int[] nums) {
int n = nums.length;
int max = Integer.MIN_VALUE, right = -1;
int min = Integer.MAX_VALUE, left = -1;
for (int i = 0; i < n; i++) {
if (nums[i] < max) {
right = i;
} else {
max = nums[i];
}
}
for(int i = n - 1; i >= 0; i--){
if(nums[i] > min) {
left = i;
}
else {
min = nums[i];
}
}
return right == -1 ? 0 : right - left + 1;
}
}
31. 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
- 例如,
arr = [1,2,3],以下这些都可以视作arr的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
- 例如,
arr = [1,2,3]的下一个排列是[1,3,2]。 - 类似地,
arr = [2,3,1]的下一个排列是[3,1,2]。 - 而
arr = [3,2,1]的下一个排列是[1,2,3],因为[3,2,1]不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
标准的 “下一个排列” 算法可以描述为:题解
- 从后向前 查找第一个 相邻升序 的元素对
(i,j),满足A[i] < A[j]。此时[j,end)必然是降序 - 在
[j,end)从后向前 查找第一个满足A[i] < A[k]的k。 - 将
A[i]与A[k]交换 - 可以断定这时
[j,end)必然是降序,逆置[j,end),使其升序 - 如果在步骤 1 找不到符合的相邻元素对,说明当前
[begin,end)为一个降序顺序,则直接跳到步骤 4
class Solution {
public void nextPermutation(int[] nums) {
//从后向前找第一次出现邻近升序的对儿 A[i] < A[j]
int i = nums.length - 2, j = nums.length - 1;
while(i >= 0 && nums[i] >= nums[j]){
i--; j--;
}
//本身就是最后一个排列(全部降序), 把整体整个翻转变升序进行返回
if(i < 0) {
reverse(nums, 0, nums.length-1);
return;
}
//从[j, end]从后向前找第一个令A[i] < A[k]的k值 (不邻近升序对儿 ,也有可能近邻)
int k;
for(k = nums.length-1; k >= j; k--){
if(nums[i] < nums[k]) break;
}
//交换i, k
swap(nums, i, k);
//nums[j,end]是降序 改为升序
reverse(nums, j, nums.length-1);
}
public void reverse(int[] nums, int l, int r){
while(l < r){
swap(nums, l, r);
l++; r--;
}
}
public void swap(int[] nums, int i, int k){
int tmp = nums[i];
nums[i] = nums[k];
nums[k] = tmp;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号