JAVA图搜索算法之DFS-BFS
图算法DFS与BFS
BFS和DFS代表对图进行遍历,即搜索的算法,搜索算法中常用的只要有两种算法:深度优先遍历(Depth-First-Search : DFS)和广度优先遍历(Breadth-First-Search : BFS)。一个图结构可以用来表示大量现实生活中的问题,比如,道路网络,计算机网络,社交网络,用户身份解析图
①DFS深度优先搜索树
200. 岛屿数量
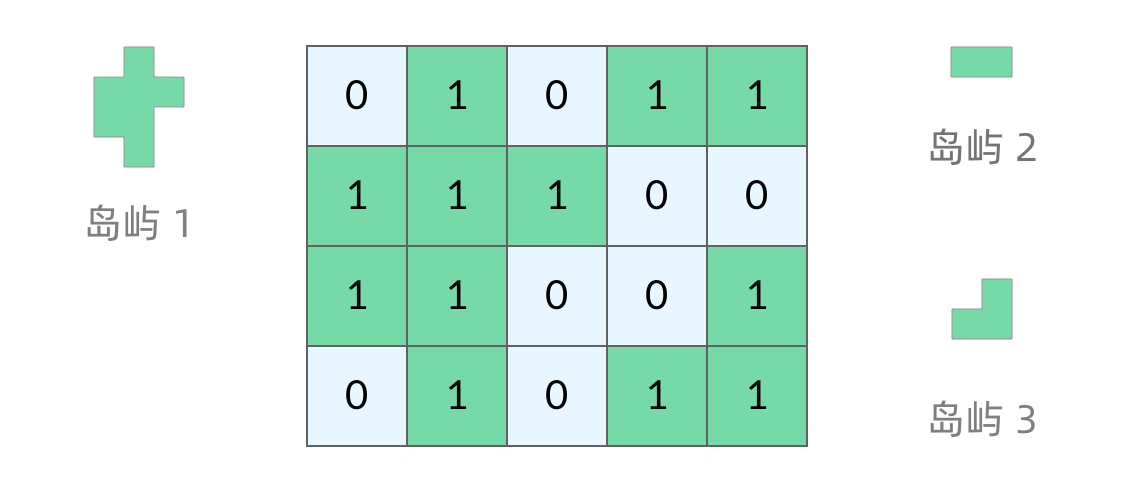
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
如何在二维矩阵中使用 DFS 搜索呢?
// 二维矩阵遍历框架
void dfs(int[][] grid, int i, int j, boolean[][] visited) {
int m = grid.length, n = grid[0].length;
// 超出索引边界
if (i < 0 || j < 0 || i >= m || j >= n) {
return;
}
// 已遍历过 (i, j)
if (visited[i][j]) {
return;
}
// 进入节点 (i, j)
visited[i][j] = true;
dfs(grid, i - 1, j, visited); // 上
dfs(grid, i + 1, j, visited); // 下
dfs(grid, i, j - 1, visited); // 左
dfs(grid, i, j + 1, visited); // 右
visited[i][j] = false;
}
因为二维矩阵本质上是一幅「图」,所以遍历的过程中需要一个 visited 布尔数组防止走回头路
- 目标是找到矩阵中 “岛屿的数量” ,即上下左右相连的
1都被认为是连续岛屿。
算法步骤:每次遇到陆地计数器加1,并把该陆地和该陆地上下左右的陆地变为海水,遍历完之后计数器就是岛屿数量
class Solution {
// 主函数,计算岛屿数量
int numIslands(char[][] grid) {
int res = 0;
int m = grid.length, n = grid[0].length;
// 遍历 grid
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == '1') {
// 每发现一个岛屿,岛屿数量加一
res++;
// 然后使用 DFS 将岛屿淹了
dfs(grid, i, j);
}
}
}
return res;
}
// 从 (i, j) 开始,将与之相邻的陆地都变成海水
void dfs(char[][] grid, int i, int j) {
int m = grid.length, n = grid[0].length;
if (i < 0 || j < 0 || i >= m || j >= n) {
// 超出索引边界
return;
}
if (grid[i][j] == '0') {
// 已经是海水了
return;
}
// 将 (i, j) 变成海水
grid[i][j] = '0';
// 淹没上下左右的陆地
dfs(grid, i + 1, j);
dfs(grid, i, j + 1);
dfs(grid, i - 1, j);
dfs(grid, i, j - 1);
}
}
为什么每次遇到岛屿,都要用 DFS 算法把岛屿「淹了」呢?主要是为了省事,避免维护 visited 数组。
因为 dfs 函数遍历到值为 0 的位置会直接返回,所以只要把经过的位置都设置为 0,就可以起到不走回头路的作用。
733. 图像渲染
有一幅以 m x n 的二维整数数组表示的图画 image ,其中 image[i][j] 表示该图画的像素值大小。
你也被给予三个整数 sr , sc 和 newColor 。你应该从像素 image[sr][sc] 开始对图像进行 上色填充 。
为了完成 上色工作 ,从初始像素开始,记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为 newColor 。
最后返回 经过上色渲染后的图像 。
示例 1:
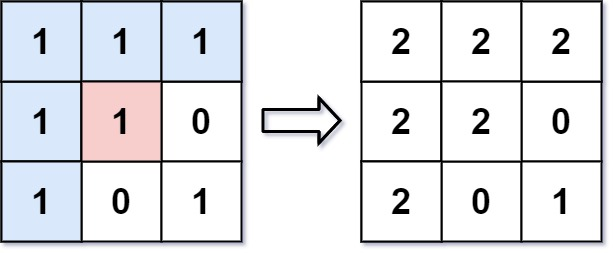
输入: image = [[1,1,1],[1,1,0],[1,0,1]],sr = 1, sc = 1, newColor = 2
输出: [[2,2,2],[2,2,0],[2,0,1]]
解析: 在图像的正中间,(坐标(sr,sc)=(1,1)),在路径上所有符合条件的像素点的颜色都被更改成2。
注意,右下角的像素没有更改为2,因为它不是在上下左右四个方向上与初始点相连的像素点。
示例 2:
输入: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2
输出: [[2,2,2],[2,2,2]]
class Solution {
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
dfs(image, sr, sc, color, image[sr][sc]);
return image;
}
public void dfs(int[][] image, int i, int j, int newColor, int oldColor){
int m = image.length, n = image[0].length;
// 超出边界
if(i < 0 || j < 0 || i >= m || j >= n) {
return;
}
// 连续的初始值才染色
if(image[i][j] != oldColor || newColor == oldColor){
return;
}
// 染色
image[i][j] = newColor;
// 遍历
dfs(image, i - 1, j, newColor, oldColor);
dfs(image, i + 1, j, newColor, oldColor);
dfs(image, i, j - 1, newColor, oldColor);
dfs(image, i, j + 1, newColor, oldColor);
}
}
1254. 统计封闭岛屿的数目
二维矩阵 grid 由 0 (土地)和 1 (水)组成。岛是由最大的4个方向连通的 0 组成的群,封闭岛是一个 完全 由1包围(左、上、右、下)的岛。
请返回 封闭岛屿 的数目。
示例 1:
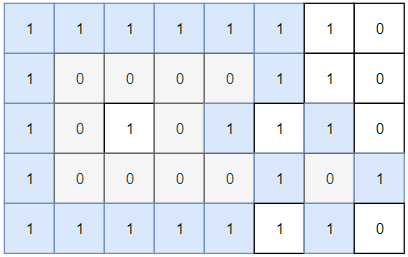
输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出:2
解释:
灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)。
示例 2:
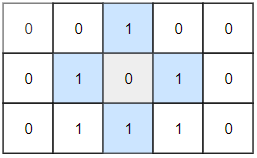
输入:grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
输出:1
示例 3:
输入:grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
输出:2
力扣第 200 题「 岛屿数量」有两点不同:
1、用 0 表示陆地,用 1 表示海水。
2、让你计算「封闭岛屿」的数目。所谓「封闭岛屿」就是上下左右全部被 1 包围的 0,也就是说靠边的陆地不算作「封闭岛屿」。
那么如何判断「封闭岛屿」呢?其实很简单,把第200题中那些靠边的岛屿排除掉,剩下的不就是「封闭岛屿」了吗?
class Solution {
public int closedIsland(int[][] grid) {
int m = grid.length, n = grid[0].length;
for(int j = 0; j < n; j++){
dfs(grid, 0, j); // 把靠上边的岛屿淹掉
dfs(grid, m - 1, j); // 把靠下边的岛屿淹掉
}
for(int i = 0; i < m; i++){
dfs(grid, i, 0); // 把靠上边的岛屿淹掉
dfs(grid, i, n - 1); // 把靠下边的岛屿淹掉
}
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == 0){
res++;
dfs(grid, i, j);
}
}
}
return res;
}
// 从 (i, j) 开始,将与之相邻的陆地都变成海水
public void dfs(int[][] grid, int i, int j) {
int m = grid.length, n = grid[0].length;
// 超出边界
if (i < 0 || j < 0 || i >= m || j >= n) {
return;
}
// 已经是海水了
if (grid[i][j] == 1) {
return;
}
// 将 (i, j) 变成海水
grid[i][j] = 1;
// 淹没上下左右的陆地
dfs(grid, i + 1, j);
dfs(grid, i, j + 1);
dfs(grid, i - 1, j);
dfs(grid, i, j - 1);
}
}
695. 岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:

img
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
给 dfs 函数设置返回值,记录每次淹没的陆地的个数
class Solution {
public int maxAreaOfIsland(int[][] grid) {
int m = grid.length, n = grid[0].length;
int max = 0; // 记录岛屿的最大面积
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == 1){
// 淹没岛屿,并更新最大岛屿面积
max = Math.max(max, dfs(grid, i, j));
}
}
}
return max;
}
// 淹没与(i,j) 相邻的陆地,并返回淹没的陆地面积
public int dfs(int[][] grid, int i, int j){
int m = grid.length, n = grid[0].length;
// 超出索引边界
if(i < 0 || j < 0 || i >= m || j >= n){
return 0;
}
// 已经是海水
if(grid[i][j] == 0){
return 0;
}
// 将(i,j)变为海水
grid[i][j] = 0;
// 淹没上下左右的陆地,并统计淹没陆地数量
int sum = 1; // 默认sum为1,如果不是岛屿,则直接返回0,就可以避免预防错误的情况。
sum += dfs(grid, i - 1, j);
sum += dfs(grid, i + 1, j);
sum += dfs(grid, i, j - 1);
sum += dfs(grid, i, j + 1);
return sum;
}
}
1020. 飞地的数量
给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
示例 1:
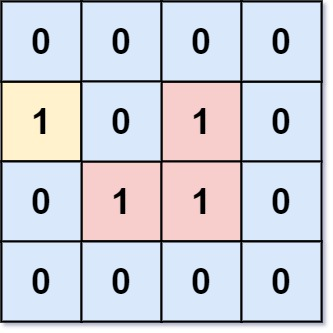
输入:grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出:3
解释:有三个 1 被 0 包围。一个 1 没有被包围,因为它在边界上。
示例 2:
img
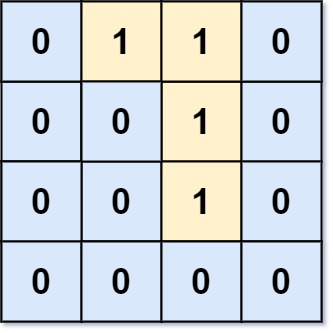
输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出:0
解释:所有 1 都在边界上或可以到达边界。
class Solution {
public int numEnclaves(int[][] grid) {
int m = grid.length, n = grid[0].length;
// 去除上下边界陆地
for(int j = 0; j < n; j++){
dfs(grid, 0, j);
dfs(grid, m - 1, j);
}
// 去除左右边界陆地
for(int i = 0; i < m; i++){
dfs(grid, i, 0);
dfs(grid, i, n - 1);
}
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j]== 1){
res++;
}
}
}
return res;
}
// 从 (i, j) 开始,将与之相邻的陆地都变成海水
public void dfs(int[][] grid, int i, int j) {
int m = grid.length, n = grid[0].length;
// 超出边界
if (i < 0 || j < 0 || i >= m || j >= n) {
return;
}
// 已经是海水了
if (grid[i][j] == 0) {
return;
}
// 将 (i, j) 变成海水
grid[i][j] = 0;
// 淹没上下左右的陆地
dfs(grid, i + 1, j);
dfs(grid, i, j + 1);
dfs(grid, i - 1, j);
dfs(grid, i, j - 1);
}
}
class Solution {
public int numEnclaves(int[][] grid) {
int m = grid.length, n = grid[0].length;
// 去除上下边界陆地
for(int j = 0; j < n; j++){
dfs(grid, 0, j);
dfs(grid, m - 1, j);
}
// 去除左右边界陆地
for(int i = 0; i < m; i++){
dfs(grid, i, 0);
dfs(grid, i, n - 1);
}
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j]== 1){
res += dfs(grid, i, j);
}
}
}
return res;
}
// 淹没与(i,j) 相邻的陆地,并返回淹没的陆地面积
public int dfs(int[][] grid, int i, int j){
int m = grid.length, n = grid[0].length;
// 超出边界
if(i < 0 || j < 0 || i >= m || j >= n){
return 0;
}
// 已是海水
if(grid[i][j] == 0){
return 0;
}
// 将(i,j)变为海水
grid[i][j] = 0;
// 淹没上下左右的陆地,并统计淹没陆地数量
int sum = 1;
sum += dfs(grid, i + 1, j);
sum += dfs(grid, i, j + 1);
sum += dfs(grid, i - 1, j);
sum += dfs(grid, i, j - 1);
return sum;
}
}
噪音传播-华为数存面试
终端产品在进行一项噪音监测实验。若将空实验室平面图视作一个N*M的二维矩阵(左上角为[0,0])。工作人员在实验室内设置了若干噪音源,并以[噪音源所在行,噪音源所在列,噪音值]的形式记录于二维数组noise中。
噪音沿相邻8个方向传播,在传播过程中,噪音值(单位为分贝)逐级递减1分贝,直至分贝削弱至1(即噪音源覆盖区域边缘噪音分贝为1);
若同一格被多个噪音源的噪音覆盖,检测结果不叠加,仅保留较大的噪音值(噪音源所在格也可能被其他噪音源的噪声传播所覆盖)。
在所有噪音源开启且持续传播情况稳定后,请监测每格噪音分贝数并返回他们的总和。
注意:
除噪音源以外的所有格初始值为0分贝;不考虑墙面反射。
示例1:
输入:n=5,m=6,noise=[[3,4,3],[1,1,4]]
输出:63
class Main {
public static void main(String[] args) {
int[][] noise = {{3,4,3}, {1,1,4}};
System.out.println(spreadNoise(5, 6, noise));
}
public static int spreadNoise(int n, int m, int[][] noise) {
int[][] grid = new int[n][m];
for (int[] num: noise) {
dfs(grid, num[0], num[1], num[2]);
}
// 统计结果
int sum = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
sum += grid[i][j];
}
}
return sum;
}
// 噪声填充
// 将(i,j)的 8 个方向填充数据
public static void dfs(int[][] grid, int row, int col, int val){
int m = grid.length, n = grid[0].length;
// 超出边界
if (row < 0 || col < 0 || row >= m || col >= n) {
return;
}
// 循环结束(val为0 或 保留较大的噪音值)
if (val == 0 || grid[row][col] >= val) {
return;
}
// 记录值
grid[row][col] = val;
// 沿8个方向扩散
dfs(grid, row + 1, col, val - 1);
dfs(grid, row - 1, col, val - 1);
dfs(grid, row, col + 1, val - 1);
dfs(grid, row, col - 1, val - 1);
dfs(grid, row + 1, col + 1, val - 1);
dfs(grid, row + 1, col - 1, val - 1);
dfs(grid, row - 1, col + 1, val - 1);
dfs(grid, row - 1, col - 1, val - 1);
}
}
79. 单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
进阶:你可以使用搜索剪枝的技术来优化解决方案,使其在 board 更大的情况下可以更快解决问题?
示例 1:
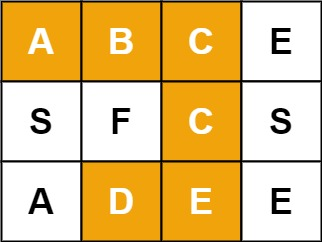
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
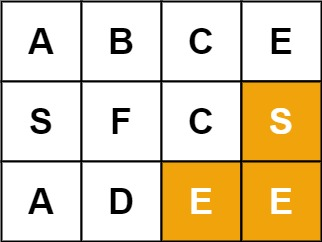
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出:true
示例 3:

输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出:false
class Solution {
public boolean exist(char[][] board, String word) {
int m = board.length, n = board[0].length;
boolean[][] visited = new boolean[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if(dfs(board, i, j, word, 0, visited)){
return true;
}
}
}
return false;
}
// 从 (i, j) 开始向四周搜索,试图匹配 word[p..]
boolean dfs(char[][] board, int i, int j, String word, int p, boolean[][] visited) {
int m = board.length, n = board[0].length;
if(p == word.length()){
return true;
}
if (i < 0 || j < 0 || i >= m || j >= n) {
// 超出索引边界
return false;
}
if(board[i][j] != word.charAt(p)){
return false;
}
if (visited[i][j]) {
// 已遍历过 (i, j)
return false;
}
// 进入节点 (i, j)
visited[i][j] = true;
boolean t = dfs(board, i - 1, j, word, p + 1, visited); // 上
boolean b = dfs(board, i + 1, j, word, p + 1, visited); // 下
boolean l = dfs(board, i, j - 1, word, p + 1, visited); // 左
boolean r = dfs(board, i, j + 1, word, p + 1, visited); // 右
visited[i][j] = false;
return t || b || l || r;
}
}
994. 腐烂的橘子
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0代表空单元格; - 值
1代表新鲜橘子; - 值
2代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例 1:

输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:grid = [[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
输入:grid = [[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
对于二维网格 grid 来说,当遍历到腐烂的🍊时,grid[i][j] == 2
定义 time 用来记录传染到该位置所需要的时间,初始化 time=2,最后要减 2,即每个格子在经过 DFS 遍历后,放的不再是🍊的情况,而是从第一个腐烂🍊的位置感染到当前位置的🍊所需要经过的分钟数,此时需要以该位置为起点找与当前遍历的腐烂的🍊相邻的 4 个位置中是否有新鲜的🍊,若有新鲜的🍊,则直接将其腐烂并且所需要的时间 time+1,即得到从起点腐烂到该位置所需要的分钟数。
class Solution {
public int orangesRotting(int[][] grid) {
int m = grid.length, n = grid[0].length;
// 网格为null或者长度为0的时候返回0;
if (grid == null || m == 0) {
return 0;
}
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 2) {
// 每次更新橘子腐烂时间是直接覆盖 grid 而 grid 中已经有2了,所以从2开始
dfs(i, j, grid, 2); // 开始传染
}
}
}
// 经过dfs后,grid数组中记录了每个橘子被传染时的时间,找出最大的时间即为腐烂全部橘子所用的时间。
int maxTime = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
return -1; // 若有新鲜橘子未被传染到,直接返回-1
} else {
maxTime = Math.max(maxTime, grid[i][j]);
}
}
}
return maxTime == 0 ? 0 : maxTime - 2;
}
// time用来记录传染时间(当然最后要减2)
private void dfs(int i, int j, int[][] grid, int time) {
int m = grid.length, n = grid[0].length;
// 超出范围
if (i < 0 || j < 0 || i >= m || j >= n) {
return;
}
// 只有新鲜橘子或者其他橘子时间time>现在time的橘子,才继续进行传播。
if (grid[i][j] != 1 && grid[i][j] < time) {
return;
}
// 将传染时间存到grid[i][j]中
grid[i][j] = time;
time++;
dfs(i - 1, j, grid, time);
dfs(i + 1, j, grid, time);
dfs(i, j - 1, grid, time);
dfs(i, j + 1, grid, time);
}
}
1905. 统计子岛屿
给你两个 m x n 的二进制矩阵 grid1 和 grid2 ,它们只包含 0 (表示水域)和 1 (表示陆地)。一个 岛屿 是由 四个方向 (水平或者竖直)上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。
如果 grid2 的一个岛屿,被 grid1 的一个岛屿 完全 包含,也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含,那么我们称 grid2 中的这个岛屿为 子岛屿 。
请你返回 grid2 中 子岛屿 的 数目 。
示例 1:
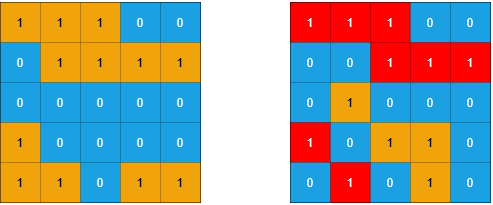
输入:grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
输出:3
解释:如上图所示,左边为 grid1 ,右边为 grid2 。
grid2 中标红的 1 区域是子岛屿,总共有 3 个子岛屿。
示例 2:

输入:grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
输出:2
解释:如上图所示,左边为 grid1 ,右边为 grid2 。
grid2 中标红的 1 区域是子岛屿,总共有 2 个子岛屿。
这道题的关键在于,如何快速判断子岛屿?
什么情况下 grid2 中的一个岛屿 B 是 grid1 中的一个岛屿 A 的子岛?
当岛屿 B 中所有陆地在岛屿 A 中也是陆地的时候,岛屿 B 是岛屿 A 的子岛。
反过来说,如果岛屿 B 中存在一片陆地,在岛屿 A 的对应位置是海水,那么岛屿 B 就不是岛屿 A 的子岛。
那么,我们只要遍历 grid2 中的所有岛屿,把那些不可能是子岛的岛屿排除掉,剩下的就是子岛。
这道题的思路和「统计封闭岛屿的数目」的思路有些类似,只不过后者排除那些靠边的岛屿,前者排除那些不可能是子岛的岛屿。
class Solution {
public int countSubIslands(int[][] grid1, int[][] grid2) {
int m = grid1.length, n = grid1[0].length;
// 将 grid2 中肯定不是子岛的,淹掉
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid1[i][j] == 0 && grid2[i][j] == 1){
dfs(grid2, i, j);
}
}
}
// 现在 grid2 中剩下的岛屿都是子岛,计算岛屿数量
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid2[i][j] == 1){
res++;
dfs(grid2, i, j);
}
}
}
return res;
}
// 从 (i, j) 开始,将与之相邻的陆地都变成海水
public void dfs(int[][] grid, int i, int j) {
int m = grid.length, n = grid[0].length;
// 超出边界
if (i < 0 || j < 0 || i >= m || j >= n) {
return;
}
// 已经是海水了
if (grid[i][j] == 0) {
return;
}
// 将 (i, j) 变成海水
grid[i][j] = 0;
// 淹没上下左右的陆地
dfs(grid, i + 1, j);
dfs(grid, i, j + 1);
dfs(grid, i - 1, j);
dfs(grid, i, j - 1);
}
}
剑指 Offer 13. 机器人的运动范围
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
class Solution {
public int movingCount(int m, int n, int k) {
boolean[][] visited = new boolean[m][n];
dfs(m, n, k, 0, 0, visited);
return res;
}
int res = 0; // 记录合法坐标数
public void dfs(int m, int n, int k, int i, int j, boolean[][] visited){
// 超出索引边界
if(i < 0 || j < 0 || i >= m || j >= n){
return;
}
// 坐标和超出 k 的限制
if(i / 10 + i % 10 + j / 10 + j % 10 > k){
return;
}
// 之前已经访问过当前坐标
if(visited[i][j]){
return;
}
res++; // 走到一个合法坐标
visited[i][j] = true;
dfs(m, n, k, i + 1, j, visited);
dfs(m, n, k, i, j + 1, visited);
dfs(m, n, k, i - 1, j, visited);
dfs(m, n, k, i, j - 1, visited);
}
}
小于n的最大整数
给一个数组,以及数字n,求arr中的数字能组成小于n的最大整数
例如A={1, 2, 4, 9},n=2533,返回2499
首先将arr数组排序,之后使用深搜+贪心的思想,从第一位开始,尽量使用与对应位置相等的数字。如果有任意一位没有使用相等的数字,那在后面的所有位中都直接使用最大的数字即可。
public class ZJtest {
static int ans; // 用于存储找到的符合条件的数字
public static void main(String[] args) {
int[] arr = {1,2,9,4};
System.out.println(find(2533, arr));
}
public static boolean dfs(int index, boolean pass, int temp, int[] arr, int n) {
String s = String.valueOf(n);
int len = s.length();
if (index == len) { // 如果已经遍历完字符串,则找到了符合条件的数字
ans = temp;
return true; // 返回true表示已经找到符合条件的数字
}
if (pass) { // 如果已经找到了比当前数字小的数字,则直接使用数组中的最大数字
return dfs(index + 1, true, temp * 10 + arr[arr.length - 1], arr, n);
} else {
int val = s.charAt(index) - '0';
for (int i = arr.length - 1; i >= 0; i--) {
if (val == arr[i]) { // 如果当前数字在数组中存在,则使用该数字继续递归查找
if (dfs(index + 1, false, temp * 10 + arr[i], arr, n)) {
return true;
}
} else if (val > arr[i]) { // 如果当前数字大于数组中的数字,则使用该数字继续递归查找
if (dfs(index + 1, true, temp * 10 + arr[i], arr, n)) {
return true;
}
}
}
if (index != 0) { // 如果当前位置不是第一位,则返回false表示没有找到符合条件的数字
return false;
}
// 如果当前位置是第一位,则使用数组中的最小数字继续递归查找
return dfs(index + 1, true, temp, arr, n);
}
}
public static int find(int N, int[] arr) {
Arrays.sort(arr);
dfs(0, false, 0, arr, N);
return ans;
}
}
dfs方法中有四个形参:index,pass,temp和arr,表示当前遍历到的字符索引位置,上一位是否能匹配当前位(即小于等于或大于当前位),已匹配数值和数组。函数返回值为布尔型。
在函数体内部,通过if else语句判断当前位数是否与数组中的数字相等或者大于目标数字,根据判断结果分别进行递归操作,直至搜索完成。如果搜索成功,就将当前匹配的数值更新到ans变量中。
- 当pass为true时,表示上一位匹配成功,当前位可以是数组中任意数字。故直接在数组的尾部数字上进行递归搜索。
- 当pass为false时,表示上一位并没有匹配成功,此时需要从大到小枚举数组中可能的数字。
- 如果当前位与数组中某一位数字相等,则可以直接与之匹配,并继续向后递归。
- 如果当前位大于数组中某一位数字,则说明需要跳过这个数字,将pass置为true,并再次递归搜索。
- 如果整个字符串都遍历完毕但还没有匹配出结果,则返回false。
最后,在dfs方法的末尾判断是否为第一个字符。如果是,说明第一个字符可以取0,即有前导零的情况,此时将pass置为true,并再次递归搜索。
整体来说,这段代码的主要功能就是对固定数字按照规定的数组进行匹配查找,返回能够匹配的最大值。
841. 钥匙和房间
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。
当你进入一个房间,你可能会在里面找到一套不同的钥匙,每把钥匙上都有对应的房间号,即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。
给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true,否则返回 false。
示例 1:
输入:rooms = [[1],[2],[3],[]]
输出:true
解释:
我们从 0 号房间开始,拿到钥匙 1。
之后我们去 1 号房间,拿到钥匙 2。
然后我们去 2 号房间,拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间,我们返回 true。
示例 2:
输入:rooms = [[1,3],[3,0,1],[2],[0]]
输出:false
解释:我们不能进入 2 号房间。
当 x 号房间中有 y 号房间的钥匙时,我们就可以从 x 号房间去往 y 号房间。如果我们将这 n 个房间看成有向图中的 n 个节点,那么上述关系就可以看作是图中的 x 号点到 y 号点的一条有向边。问题就变成了给定一张有向图,询问从 0 号节点出发是否能够到达所有的节点。
DFS
我们可以使用深度优先搜索的方式遍历整张图,统计可以到达的节点个数,并利用数组 visited 标记当前节点是否访问过,以防止重复访问。
class Solution {
boolean[] visited; // 房间是否访问过
int num; // 已访问房间数
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
int n = rooms.size();
num = 0;
visited = new boolean[n];
dfs(rooms, 0); // 从 0 号房开始访问
return num == n;
}
public void dfs(List<List<Integer>> rooms, int x) {
visited[x] = true;
num++;
for (int i : rooms.get(x)) {
if (!visited[i]) { // 若该房间未被访问过
dfs(rooms, i);
}
}
}
}
BFS
我们也可以使用广度优先搜索的方式遍历整张图,统计可以到达的节点个数,并利用数组 visited 标记当前节点是否访问过,以防止重复访问。
class Solution {
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
int n = rooms.size();
int num = 0;
boolean[] visited = new boolean[n];
Queue<Integer> queue = new LinkedList<Integer>();
queue.offer(0);
visited[0] = true;
while (!queue.isEmpty()) {
int x = queue.poll();
num++;
for (int i : rooms.get(x)) {
if (!visited[i]) {
visited[i] = true;
queue.offer(i);
}
}
}
return num == n;
}
}
547. 省份数量
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
示例 1:

img
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出:2
示例 2:

img
输入:isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出:3
可以把 n 个城市和它们之间的相连关系看成图,城市是图中的节点,相连关系是图中的边,给定的矩阵 isConnected即为图的邻接矩阵,省份即为图中的连通分量。
计算省份总数,等价于计算图中的连通分量数,可以通过深度优先搜索或广度优先搜索实现,也可以通过并查集实现。
DFS
遍历所有城市,对于每个城市,如果该城市尚未被访问过,则从该城市开始深度优先搜索,通过矩阵 isConnected 得到与该城市直接相连的城市有哪些,这些城市和该城市属于同一个连通分量,然后对这些城市继续深度优先搜索,直到同一个连通分量的所有城市都被访问到,即可得到一个省份。遍历完全部城市以后,即可得到连通分量的总数,即省份的总数。
class Solution {
public int findCircleNum(int[][] isConnected) {
int cities = isConnected.length;
boolean[] visited = new boolean[cities];
int provinces = 0;
for (int i = 0; i < cities; i++) {
if (!visited[i]) {
dfs(isConnected, visited, cities, i);
provinces++;
}
}
return provinces;
}
public void dfs(int[][] isConnected, boolean[] visited, int cities, int i) {
for (int j = 0; j < cities; j++) {
if (isConnected[i][j] == 1 && !visited[j]) {
visited[j] = true;
dfs(isConnected, visited, cities, j);
}
}
}
}
BFS
对于每个城市,如果该城市尚未被访问过,则从该城市开始广度优先搜索,直到同一个连通分量中的所有城市都被访问到,即可得到一个省份。
class Solution {
public int findCircleNum(int[][] isConnected) {
int cities = isConnected.length;
boolean[] visited = new boolean[cities];
int provinces = 0;
Queue<Integer> queue = new LinkedList<Integer>();
for (int i = 0; i < cities; i++) {
if (!visited[i]) {
queue.offer(i);
while (!queue.isEmpty()) {
int k = queue.poll();
visited[k] = true;
for (int j = 0; j < cities; j++) {
if (isConnected[k][j] == 1 && !visited[j]) {
queue.offer(j);
}
}
}
provinces++;
}
}
return provinces;
}
}
1466. 重新规划路线
n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,以改变交通拥堵的状况。
路线用 connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年,城市 0 将会举办一场大型比赛,很多游客都想前往城市 0 。
请你帮助重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
示例 1:

输入:n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出:3
解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
示例 2:

输入:n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出:2
解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
示例 3:
输入:n = 3, connections = [[1,0],[2,0]]
输出:0
我们可以将这个图看做是无向图,从0城市开始往外走,走到哪个城市后看下与原有道路的方向是否相反,如果相反代表不用改变路线的方向,如果不相反则需要改变路线的方向(因为我们是从0开始走,走的方向是对外的,而其他城市想来0城市,肯定是往里走,路线方向应该与我们往外走的方式相反),然后统计需要改变方向的路线数即可。
// 建立无向图,使用邻接表存图,并使用一个额外标记记录边的方向
class Solution {
Map<Integer, List<int[]>> map = new HashMap<>();
boolean[] visited;
// direction记录该边和原始边的方向, 1 表示同向,0 表示反向
void add(int i, int j, int direction) {
if (!map.containsKey(i)) {
map.put(i, new ArrayList<>());
}
map.get(i).add(new int[]{j, direction});
}
public int minReorder(int n, int[][] connections) {
// 建立无向图
for (int[] connection : connections) {
int i = connection[0], j = connection[1];
add(i, j, 1);
add(j, i, 0);
}
visited = new boolean[n];
// 若某个子节点是通过反向边到达的,则该边不用变更方向,
// 若某个子节点是通过正向边到达的,则该边需要变更方向
// 所以树中同向边的数量就是需要变更方向的路线数,则对做根节点 0 进行dfs遍历可得结果
return dfs(0);
}
// 返回当前节点中对应子树中同向边的数量
int dfs(int node) {
visited[node] = true;
List<int[]> edges = map.get(node);
int count = 0;
for (int[] edge : edges) {
int child = edge[0], direction = edge[1];
if (!visited[child]) {
count += direction + dfs(child);
}
}
return count;
}
}
399. 除法求值
给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件,其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。
另有一些以数组 queries 表示的问题,其中 queries[j] = [Cj, Dj] 表示第 j 个问题,请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。
返回 所有问题的答案 。如果存在某个无法确定的答案,则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串,也需要用 -1.0 替代这个答案。
示例 1:
输入:equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出:[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释:
条件:a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果:[6.0, 0.5, -1.0, 1.0, -1.0 ]
示例 2:
输入:equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出:[3.75000,0.40000,5.00000,0.20000]
示例 3:
输入:equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出:[0.50000,2.00000,-1.00000,-1.00000]
我们可以将整个问题建模成一张图:给定图中的一些点(变量),以及某些边的权值(两个变量的比值),试对任意两点(两个变量)求出其路径长(两个变量的比值)。
因此,我们首先需要遍历 equations\textit{equations}equations 数组,找出其中所有不同的字符串,并通过哈希表将每个不同的字符串映射成整数。
在构建完图之后,对于任何一个查询,就可以从起点出发,通过广度优先搜索的方式,不断更新起点与当前点之间的路径长度,直到搜索到终点为止。
视频指路链接:https://www.bilibili.com/video/BV1XU4y1s7Lk
class Solution {
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
//初始化Graph(以HashMap形式)
Map<String, List<Cell>> graph = new HashMap<>();
//对于每个Equation和其结果答案,将其加入Graph中
// 对于每个点,存储其直接连接到的所有点及对应的权值
for(int i = 0; i < values.length; i++) {
String s1 = equations.get(i).get(0), s2 = equations.get(i).get(1);
graph.computeIfAbsent(s1, k -> new ArrayList<>()).add(new Cell(s2, values[i]));
graph.computeIfAbsent(s2, k -> new ArrayList<>()).add(new Cell(s1, 1.0 / values[i]));
}
//创建答案result数组以及访问过的HashSet: visited
double[] res = new double[queries.size()];
//首先将答案中所有答案值置为-1.0,出现(x / x)情况可以直接不用修改
Arrays.fill(res, -1.0);
//对于每个query中的值调用dfs函数
for(int i = 0; i < queries.size(); i++) {
dfs(queries.get(i).get(0), queries.get(i).get(1), 1.0, graph, res, i, new HashSet<>());
}
return res;
}
//src: 当前位置; dst: 答案节点; cur: 当前计算值; graph: 之前建的图; res: 答案array; index: 当前遍历到第几个query; visited: 查重Set
private void dfs(String src, String dst, double cur, Map<String, List<Cell>> graph, double[] res, int index, Set<String> visited) {
//base case: 在visited中加入当前位置信息;如果加不了代表已经访问过,直接返回
if(!visited.add(src)) {
return;
}
//如果当前位置src = 答案节点dst,并且此节点在graph中(避免x/x的情况),用当前计算值cur来填充答案res[index]
if(src.equals(dst) && graph.containsKey(src)) {
res[index] = cur;
return;
}
//对于邻居节点,调用dfs函数
for(Cell nei : graph.getOrDefault(src, new ArrayList<>())) {
dfs(nei.str, dst, cur * nei.div, graph, res, index, visited);
}
}
}
class Cell {
String str;
double div;
Cell(String str, double div) {
this.str = str;
this.div = div;
}
}
②BFS
算法框架
我们先举例一下 BFS 出现的常见场景好吧,问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿。
这个广义的描述可以有各种变体,比如走迷宫,有的格子是围墙不能走,从起点到终点的最短距离是多少?如果这个迷宫带「传送门」可以瞬间传送呢?
再比如说两个单词,要求你通过某些替换,把其中一个变成另一个,每次只能替换一个字符,最少要替换几次?
再比如说连连看游戏,两个方块消除的条件不仅仅是图案相同,还得保证两个方块之间的最短连线不能多于两个拐点。你玩连连看,点击两个坐标,游戏是如何判断它俩的最短连线有几个拐点的?
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue<Node> q; // 核心数据结构
Set<Node> visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur == target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj()) {
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
}
}
// 如果走到这里,说明在图中没有找到目标节点
}
cur.adj() 泛指 cur 相邻的节点,比如说二维数组中,cur 上下左右四面的位置就是相邻节点;visited 的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要 visited。
1926. 迷宫中离入口最近的出口
给你一个 m x n 的迷宫矩阵 maze (下标从 0 开始),矩阵中有空格子(用 '.' 表示)和墙(用 '+' 表示)。同时给你迷宫的入口 entrance ,用 entrance = [entrancerow, entrancecol] 表示你一开始所在格子的行和列。
每一步操作,你可以往 上,下,左 或者 右 移动一个格子。你不能进入墙所在的格子,你也不能离开迷宫。你的目标是找到离 entrance 最近 的出口。出口 的含义是 maze 边界 上的 空格子。entrance 格子 不算 出口。
请你返回从 entrance 到最近出口的最短路径的 步数 ,如果不存在这样的路径,请你返回 -1 。
示例 1:

输入:maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
输出:1
解释:总共有 3 个出口,分别位于 (1,0),(0,2) 和 (2,3) 。
一开始,你在入口格子 (1,2) 处。
- 你可以往左移动 2 步到达 (1,0) 。
- 你可以往上移动 1 步到达 (0,2) 。
从入口处没法到达 (2,3) 。
所以,最近的出口是 (0,2) ,距离为 1 步。
示例 2:

输入:maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
输出:2
解释:迷宫中只有 1 个出口,在 (1,2) 处。
(1,0) 不算出口,因为它是入口格子。
初始时,你在入口与格子 (1,0) 处。
- 你可以往右移动 2 步到达 (1,2) 处。
所以,最近的出口为 (1,2) ,距离为 2 步。
示例 3:

img
输入:maze = [[".","+"]], entrance = [0,0]
输出:-1
解释:这个迷宫中没有出口。
标准的 BFS 算法,只要套用 BFS 算法模板框架就可以了
class Solution {
public int nearestExit(char[][] maze, int[] entrance) {
int m = maze.length;
int n = maze[0].length;
int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};// 右左下上
// BFS 算法的队列和 visited 数组
Queue<int[]> queue = new LinkedList<>();
boolean[][] visited = new boolean[m][n];
queue.offer(entrance);
visited[entrance[0]][entrance[1]] = true;
// 启动 BFS 算法从 entrance 开始像四周扩散
int step = 0;
while (!queue.isEmpty()) {
int sz = queue.size();
step++;
// 扩散当前队列中的所有节点
for (int i = 0; i < sz; i++) {
int[] cur = queue.poll();
// 每个节点都会尝试向上下左右四个方向扩展一步
for (int[] dir : dirs) {
int x = cur[0] + dir[0];
int y = cur[1] + dir[1];
if (x < 0 || x >= m || y < 0 || y >= n
|| visited[x][y] || maze[x][y] == '+') {
continue;
}
if (x == 0 || x == m - 1 || y == 0 || y == n - 1) {
// 走到边界(出口)
return step;
}
visited[x][y] = true;
queue.offer(new int[]{x, y});
}
}
}
return -1;
}
}
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
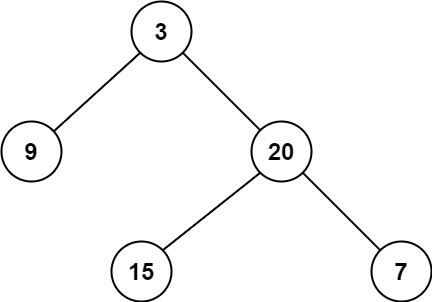
输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
// 时间复杂度:O(N)
// 空间复杂度:O(N)
class Solution {
public int minDepth(TreeNode root) {
if(root == null) return 0;
Queue<TreeNode> queue = new LinkedList<>();
int depth = 1;
queue.offer(root);
while(!queue.isEmpty()){
int n = queue.size();
depth++;
while(n > 0){
TreeNode node = queue.poll();
if(node.left != null) queue.offer(node.left);
if(node.right != null) queue.offer(node.right);
if(node.left == null && node.right == null){
return depth;
}
n--;
}
}
return depth;
}
}







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix