Java-全网最详细数据结构
数构&算法:数据结构
- 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关,以下是各种数据结构的详细说明。
线性结构:数组、队列、链表、栈
顺序存储(地址连续)
链式存储(地址不一定连续)
非线性结构:二维数组、多维数组、广义表、树、图
①数组
❶稀疏数组
- 稀疏数组是一种用来压缩数据量的数据结构,简而言之,就是记录特殊值,然后剩下大量重复的数据可以消减。
例如下方是一个普通二维数组
0 0 0 0 0 0
0 0 1 0 0 0
0 0 0 2 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
这么一个二维数组,化成稀疏数组可以表示为:
行 列 值
0 6 6 2
1 1 2 1
2 2 3 2
1. 稀疏数组第一行表示原数组有多少行,多少列,有多少个非零元素(有效值)
2. 稀疏数组是从0开始的
3. 稀疏数组的行数等于有效值+1,列数固定都为3
二维数组转稀疏数组的步骤:
- 遍历二维数组,得到有效值个数 sum
- 根据 sum 创建稀疏数组 sparseArr = int [sum+1][3]
- 将有效值存入稀疏数组
还原稀疏数组步骤:
- 创建一个新的数组,其行和列等于稀疏数组首行数据
- 遍历稀疏数组,将对应数值赋值给新的数组
- 最后可以验证一下原始的数组和还原后的数组是否相等
//稀疏数组:用来减少数据量
public class SparseArray {
public static void main(String[] args) {
// 一、构建原始数组
// 创建一个二维数组6*6 0:没有棋子,1:黑棋 2:白棋
int[][] chessArr = new int[6][6];
chessArr[1][2] = 1;
chessArr[2][3] = 2;
System.out.println("原始数组:");
for (int[] row : chessArr) {
for (int data : row) {
System.out.print(data+"\t");
}
System.out.println();
}
System.out.println("====================");
// 二、转换成稀疏数组
int sum = 0;
//1.先遍历二维数组,获取有效值的个数
for (int i = 0; i < chessArr.length; i++) {
for (int j = 0; j < chessArr[0].length; j++) {
if(chessArr[i][j] != 0) {
sum++;//有效值的个数
}
}
}
//2.创建对应稀疏数组
int [][]sparseArr = new int[sum+1][3];
//第一行赋值
sparseArr[0][0] = chessArr.length;
sparseArr[0][1] = chessArr[0].length;
sparseArr[0][2] = sum;
//3.遍历初始的二维数组,将非零的值,存放到稀疏数组中
int count = 0;
for (int i = 0; i < chessArr.length; i++) {
for (int j = 0; j < chessArr[0].length; j++) {
if (chessArr[i][j] != 0){
count++;
sparseArr[count][0] = i;
sparseArr[count][1] = j;
sparseArr[count][2] = chessArr[i][j];
}
}
}
//4.输出稀疏数组
System.out.println("稀疏数组:");
for (int i = 0; i < sparseArr.length; i++) {
System.out.println(sparseArr[i][0]+"\t"+sparseArr[i][1]+"\t"+sparseArr[i][2]+"\t");
}
// 三、还原数组
int [][] ChessArr2 = new int[sparseArr[0][0]][sparseArr[0][1]];
for (int i = 1; i < sparseArr.length; i++) {
ChessArr2[sparseArr[i][0]][sparseArr[i][1]] = sparseArr[i][2];
}
System.out.println("=======================");
//打印还原的数组
System.out.println("输出还原后的数组:");
for (int[] row : ChessArr2) {
for (int data : row) {
System.out.print(data+"\t");
}
System.out.println();
}
//四、验证两个数组是否相等,可用Arrays工具类
int flag = 0;
for (int i = 0; i < chessArr.length; i++) {
if (!Arrays.equals(chessArr[i],ChessArr2[i])){
flag++;
}
}
if (flag==0){
System.out.println("初始数组和还原后的数组相等");
}
}
}
❷数组模拟队列
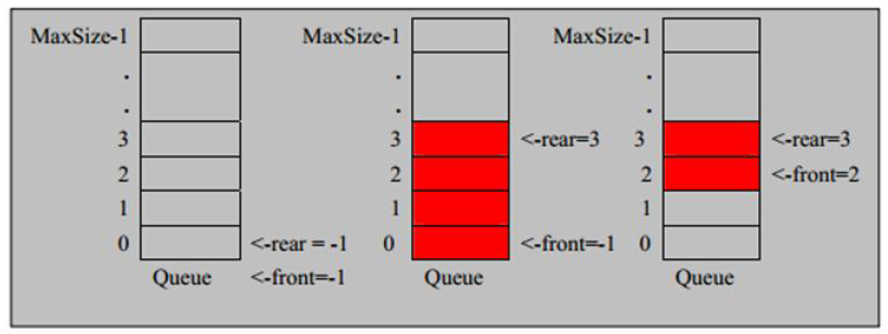
队列本身是有序列表,若使用数组的结构来存储队列的数据,则队列数组的声明如下图
maxSize 是该队列的最大容量,两个变量 front 及 rear 分别记录队列前后端的下标
class ArrayQueue {
private int MaxSize; // 队列大小
private int front; // 队列头
private int rear; // 队列尾
private int[] arr; // 数组存放数据
// 一、创建队列的构造器
public ArrayQueue(int MaxSize) {
this.MaxSize = MaxSize;
arr = new int[this.MaxSize];
front = -1;
rear = -1;
}
//二、判断队列是否满
public boolean isFull() {
return rear == MaxSize - 1;
}
//三、判断队列是否空
public boolean isEmpty() {
return rear == front;
}
//四、入队
public void addQueue(int num) {
if (isFull()) {
System.out.println("队列已满,无法在进行入队操作");
return;
}
arr[++rear] = num;
}
//五、出队
public int getQueue() {
if (isEmpty()) {
throw new RuntimeException("队列为空,无法出队");
}
return arr[++front];
}
//六、显示队列数据
public void showQueue() {
if (isEmpty()) {
throw new RuntimeException("队列为空,无法遍历");
}
for (int i = front+1; i < arr.length; i++) {
System.out.printf("arr[%d]=%d\n", i, arr[i]);
}
}
//七、显示队列头数据
public int headQueue() {
if (isEmpty()) {
throw new RuntimeException("队列为空,没有数据");
}
return arr[front + 1];
}
}
测试
public class ArrayQueueDemo {
public static void main(String[] args) {
// 构造队列
ArrayQueue queue = new ArrayQueue(5);
// 入队
queue.addQueue(1);
queue.addQueue(2);
queue.addQueue(3);
queue.addQueue(4);
queue.addQueue(5);
// 出队
System.out.println(queue.getQueue());
// 遍历队列
queue.showQueue();
// 队首
System.out.println(queue.headQueue());
}
}
②链表
❶单向链表
特点
- 链表是以节点的方式来存储,是链式存储
- 每个节点包含 data 域 (存储数据),next 域(指向下一个节点)
- 链表的各个节点不一定是连续存储的
- 链表分带头节点的链表和没有头节点的链表,根据实际的需求来确定
/**
* 定义节点
*/
class StudentNode {
int id;
String name;
StudentNode next;
public StudentNode(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "StudentNode{" +
"id=" + id +
", name='" + name + '\'' +
'}';
}
}
/**
* 创建链表
*/
class singleLinkedList {
//头节点,防止被修改,设置为私有的
private StudentNode head = new StudentNode(0, "");
//插入节点
public void addNode(StudentNode node) {
//因为头节点不能被修改,所以创建一个辅助节点
StudentNode temp = head;
//找到最后一个节点
while (temp.next != null) {
temp = temp.next;
}
temp.next = node;
}
//按id顺序插入节点
public void addByOrder(StudentNode node) {
//如果没有首节点,就直接插入
if (head.next == null) {
head.next = node;
return;
}
//辅助节点,用于找到插入位置和插入操作
StudentNode temp = head;
//节点的下一个节点存在,且它的id小于要插入节点的id,就继续下移
while (temp.next != null && temp.next.id < node.id) {
temp = temp.next;
}
//如果temp的下一个节点存在,则执行该操作
//且插入操作,顺序不能换
if (temp.next != null) {
node.next = temp.next;
}
temp.next = node;
}
//遍历链表
public void traverseNode() {
if (head.next == null) {
System.out.println("链表为空");
}
StudentNode temp = head;
while (temp.next != null) {
System.out.println(temp.next);
temp = temp.next;
}
}
//根据id来修改节点信息
public void changeNode(StudentNode node) {
if (head == null) {
System.out.println("链表为空,请先加入该学生信息");
return;
}
StudentNode temp = head;
//遍历链表,找到要修改的节点
while (temp.next != null && temp.id != node.id) {
temp = temp.next;
}
//如果temp已经是最后一个节点,判断id是否相等
if (temp.id != node.id) {
System.out.println("未找到该学生的信息,请先创建该学生的信息");
return;
}
//修改信息
temp.name = node.name;
}
//删除节点
public void deleteNode(StudentNode node) {
if (head.next == null) {
System.out.println("链表为空");
return;
}
StudentNode temp = head;
//遍历链表,找到要删除的节点
while (temp.next != null && temp.next.id != node.id) {
temp = temp.next;
}
if(temp.next == null){
System.out.println("要删除的节点不存在");
return;
}
//删除该节点
temp.next = temp.next.next;
}
//得到第index个的节点
public StudentNode getNodeByIndex(int index) {
if (head.next == null) {
System.out.println("链表为空!");
}
StudentNode temp = head;
int length = 0;
while (temp.next != null) {
temp = temp.next;
length++;
}
if (index > length) {
throw new RuntimeException("链表越界");
}
temp = head;
for (int i = 0; i < index; i++) {
temp = temp.next;
}
return temp;
}
//逆序遍历
public void reverseTraverse() {
if (head == null) {
System.out.println("链表为空");
}
StudentNode temp = head;
//创建栈,用于存放遍历到的节点
Stack<StudentNode> stack = new Stack<>();
while (temp.next != null) {
stack.push(temp.next);
temp = temp.next;
}
while (!stack.isEmpty()) {
System.out.println(stack.pop());
}
}
}
public class SingleLinkedListDemo {
public static void main(String[] args) {
singleLinkedList linkedList = new singleLinkedList();
//创建学生节点,并插入链表
System.out.println("插入节点1和3:");
StudentNode student1 = new StudentNode(1, "Jack");
StudentNode student3 = new StudentNode(3, "Tom");
linkedList.addNode(student1);
linkedList.addNode(student3);
linkedList.traverseNode();
//按id大小插入
System.out.println("有序插入节点2:");
StudentNode student2 = new StudentNode(2, "Jerry");
linkedList.addByOrder(student2);
linkedList.traverseNode();
//按id修改学生信息
System.out.println("修改节点1信息:");
student2 = new StudentNode(1, "Jack2");
linkedList.changeNode(student2);
linkedList.traverseNode();
//获得第2个节点
System.out.println("获得第2个节点:");
System.out.println(linkedList.getNodeByIndex(2));
//根据id删除学生信息
System.out.println("删除学生信息:");
student2 = new StudentNode(1, "Jack2");
linkedList.deleteNode(student2);
linkedList.traverseNode();
//倒叙遍历链表
System.out.println("倒序遍历链表:");
linkedList.reverseTraverse();
}
}
链表为空
插入节点1和3:
StudentNode{id=1, name='Jack'}
StudentNode{id=3, name='Tom'}
有序插入节点2:
StudentNode{id=1, name='Jack'}
StudentNode{id=2, name='Jerry'}
StudentNode{id=3, name='Tom'}
修改节点1信息:
StudentNode{id=1, name='Jack2'}
StudentNode{id=2, name='Jerry'}
StudentNode{id=3, name='Tom'}
获得第2个节点:
StudentNode{id=2, name='Jerry'}
删除学生信息:
StudentNode{id=2, name='Jerry'}
StudentNode{id=3, name='Tom'}
倒序遍历链表:
StudentNode{id=3, name='Tom'}
StudentNode{id=2, name='Jerry'}
❷双向链表
/**
* 定义节点
*/
class HeroNode {
int id;
String name;
HeroNode next;
HeroNode pre;
public HeroNode(int id, String name) {
this.id = id;
this.name = name;
}
@Override
public String toString() {
return "HeroNode{id=" + id + ", name=" + name + "}";
}
}
/**
* 创建一个双向链表的类
*/
class DoubleLinkedList {
//初始化一个头节点,头节点不动,不存放具体的数据
HeroNode head = new HeroNode(0, "");
//初始化一个尾节点,指向最后一个元素,默认等于head
HeroNode tail = head;
//遍历打印双向链表的方法
public void list() {
if (head.next == null) {
System.out.println("链表为空");
return;
}
HeroNode temp = head.next;
while (temp != null) {
System.out.println(temp);
temp = temp.next;
}
}
//新增节点
public void add(HeroNode heroNode) {
tail.next = heroNode;
heroNode.pre = tail;
tail = heroNode;
}
//有序新增节点
public void addByOrder(HeroNode heroNode) {
HeroNode temp = head;
// 标记添加的编号是否已经存在
boolean flag = false;
while (temp.next != null && temp.next.id <= heroNode.id) {
if (temp.next.id == heroNode.id) {
flag = true;
}
temp = temp.next;
}
// 判断flag
if (flag) {
System.out.printf("英雄编号【%d】已经存在了\n", heroNode.id);
} else {
// 插入到链表中
// 1、将【heroNode的next】设置为【temp的next】
heroNode.next = temp.next;
// 判断是不是加在链表最后
if (temp.next != null) {
// 2、将【temp的next的pre】设为为【heroNode】
temp.next.pre = heroNode;
}
// 3、将【temp的next】设置为【heroNode】
temp.next = heroNode;
// 4、将【heroNode的pre】设置为【temp】
heroNode.pre = temp;
}
}
//修改节点
public void update(HeroNode heroNode) {
// 判断是否为空
if (head.next == null) {
System.out.println("链表为空~~");
return;
}
// 找到需要修改的节点
HeroNode temp = head.next;
// 表示是否找到这个节点
boolean flag = false;
while (temp != null) {
if (temp.id == heroNode.id) {
flag = true;
break;
}
temp = temp.next;
}
// 根据flag判断是否找到要修改的节点
if (flag) {
temp.name = heroNode.name;
} else { // 没有找到
System.out.printf("没有找到编号为 %d 的节点,不能修改\n", heroNode.id);
}
}
//删除节点
public void delete(int id) {
// 判断当前链表是否为空
if (head.next == null) {
System.out.println("链表为空,无法删除");
return;
}
HeroNode temp = head;
// 标志是否找到删除节点
boolean flag = false;
while (temp.next != null) {
// 已经找到链表的最后
if (temp.id == id) {
// 找到待删除节点
flag = true;
break;
}
temp = temp.next;
}
// 判断flag,此时找到要删除的节点就是temp
if (flag) {
// 可以删除,将【temp的pre的next域】设置为【temp的next域】
temp.pre.next = temp.next;
// 如果是最后一个节点,就不需要指向下面这句话,否则会出现空指针 temp.next.pre = null.pre
if (temp.next != null) {
temp.next.pre = temp.pre;
}
}
}
}
public class DoubleLinkedListDemo {
public static void main(String[] args) {
System.out.println("双向链表:");
// 创建节点
HeroNode her1 = new HeroNode(1, "宋江");
HeroNode her2 = new HeroNode(2, "卢俊义");
HeroNode her3 = new HeroNode(3, "吴用");
HeroNode her4 = new HeroNode(4, "林冲");
// 创建一个双向链表对象
DoubleLinkedList doubleLinkedList = new DoubleLinkedList();
doubleLinkedList.add(her1);
doubleLinkedList.add(her2);
doubleLinkedList.add(her3);
doubleLinkedList.add(her4);
doubleLinkedList.list();
// 修改
HeroNode newHeroNode = new HeroNode(4, "公孙胜");
doubleLinkedList.update(newHeroNode);
System.out.println("修改节点4:");
doubleLinkedList.list();
// 删除
doubleLinkedList.delete(3);
System.out.println("删除节点3");
doubleLinkedList.list();
// 测试有序新增
System.out.println("测试有序增加链表:");
DoubleLinkedList doubleLinkedList1 = new DoubleLinkedList();
doubleLinkedList1.addByOrder(her3);
doubleLinkedList1.addByOrder(her2);
doubleLinkedList1.addByOrder(her2);
doubleLinkedList1.addByOrder(her4);
doubleLinkedList1.addByOrder(her4);
doubleLinkedList1.addByOrder(her2);
doubleLinkedList1.addByOrder(her1);
doubleLinkedList1.list();
}
}
双向链表:
HeroNode{id=1, name=宋江}
HeroNode{id=2, name=卢俊义}
HeroNode{id=3, name=吴用}
HeroNode{id=4, name=林冲}
修改节点4:
HeroNode{id=1, name=宋江}
HeroNode{id=2, name=卢俊义}
HeroNode{id=3, name=吴用}
HeroNode{id=4, name=公孙胜}
删除节点3
HeroNode{id=1, name=宋江}
HeroNode{id=2, name=卢俊义}
HeroNode{id=4, name=公孙胜}
测试有序增加链表:
英雄编号【2】已经存在了
英雄编号【4】已经存在了
英雄编号【2】已经存在了
HeroNode{id=1, name=宋江}
HeroNode{id=2, name=卢俊义}
HeroNode{id=3, name=吴用}
HeroNode{id=4, name=公孙胜}
❸循环链表
③栈&队列&堆
❶普通队列-Queue
队列是一种先进先出的数据结构,元素从后端入队,然后从前端出队。
Queue<> queue = new LinkedList<>();
常用方法
| 函数 | 功能 |
|---|---|
| add(E e)/offer(E e) | 压入元素 |
| remove()/poll() | 弹出元素 |
| element()/peek() | 获取队头元素 |
| isEmpty() | 用于检查此队列是“空”还是“非空” |
| size() | 获取队列长度 |
❷双端队列-Deque
Java集合提供了接口Deque来实现一个双端队列,它的功能是:
- 既可以添加到队尾,也可以添加到队首;
- 既可以从队首获取,又可以从队尾获取。
Deque有三种用途
- 普通队列(一端进另一端出):
Deque<> queue = new LinkedList<>();
// 等价
Queue<> queue = new LinkedList<>();
| Queue方法 | 等效Deque方法 |
|---|---|
| add(e) | addLast(e) |
| offer(e) | offerLast(e) |
| remove() | removeFirst() |
| poll() | pollFirst() |
| element() | getFirst() |
| peek() | peekFirst() |
- 双端队列(两端都可进出)
//底层:ArrayDeque(动态数组)和 LinkedList(链表)
Deque<Integer> deque = new ArrayDeque<>();
Deque<Integer> deque = new LinkedList<>();
| 第一个元素 (头部) | 最后一个元素 (尾部) | |
|---|---|---|
| 插入 | addFirst(e)/offerFirst(e) | addLast(e)/offerLast(e) |
| 删除 | removeFirst()/pollFirst() | removeLast()/pollLast() |
| 获取 | getFirst()/peekFirst() | getLast()/peekLast() |
- 堆栈(先进后出)
//底层:ArrayDeque(动态数组)和 LinkedList(链表)
Deque<Integer> stack = new LinkedList<>();
Deque<Integer> stack = new ArrayDeque<>(); //速度更快
// 等价
Stack<String> stack=new Stack<>();
| 堆栈方法 | 等效Deque方法 |
|---|---|
| push(e) | addFirst(e) |
| pop() | removeFirst() |
| peek() | peekFirst() |
Deque所有方法
| 方法 | 描述 |
|---|---|
| 添加功能 | |
| push(E) | 向队列头部插入一个元素,失败时抛出异常 |
| addFirst(E) | 向队列头部插入一个元素,失败时抛出异常 |
| addLast(E) | 向队列尾部插入一个元素,失败时抛出异常 |
| offerFirst(E) | 向队列头部加入一个元素,失败时返回false |
| offerLast(E) | 向队列尾部加入一个元素,失败时返回false |
| 获取功能 | |
| peek() | 获取队列头部元素,队列为空时抛出异常 |
| getFirst() | 获取队列头部元素,队列为空时抛出异常 |
| getLast() | 获取队列尾部元素,队列为空时抛出异常 |
| peekFirst() | 获取队列头部元素,队列为空时返回null |
| peekLast() | 获取队列尾部元素,队列为空时返回null |
| 删除功能 | |
| removeFirstOccurrence(Object) | 删除第一次出现的指定元素,不存在时返回false |
| removeLastOccurrence(Object) | 删除最后一次出现的指定元素,不存在时返回false |
| 弹出功能 | |
| pop() | 弹出队列头部元素,队列为空时抛出异常 |
| removeFirst() | 弹出队列头部元素,队列为空时抛出异常 |
| removeLast() | 弹出队列尾部元素,队列为空时抛出异常 |
| pollFirst() | 弹出队列头部元素,队列为空时返回null |
| pollLast() | 弹出队列尾部元素,队列为空时返回null |
❸优先队列-PriorityQueue
优先级队列其实就是一个披着队列外衣的堆,因为优先队列对外接口只是从队头取元素,从队尾添加元素,再无其他取元素的方式,看起来就是一个队列。
PriorityQueue 是具有优先级别的队列,优先级队列的元素按照它们的自然顺序排序,或者由队列构造时提供的 Comparator 进行排序,这取决于使用的是哪个构造函数
| 构造函数 | 描述 |
|---|---|
| PriorityQueue() | 使用默认的容量(11)创建一个优队列,元素的顺序规则采用的是自然顺序 |
| PriorityQueue(int initialCapacity) | 使用默认指定的容量创建一个优队列,元素的顺序规则采用的是自然顺序 |
| PriorityQueue(Comparator<? super E> comparator) | 使用默认的容量队列,元素的顺序规则采用的是 comparator |
//默认按自然顺序(升序)检索的
PriorityQueue<Integer> numbers = new PriorityQueue<>();
PriorityQueue<Integer> numbers = new PriorityQueue<>(3); //大小为3
//使用Comparator接口自定义此顺序
PriorityQueue<int[]> queue = new PriorityQueue<int[]>(new Comparator<int[]>() {
public int compare(int[] m, int[] n) {
return m[1] - n[1];
}
});
常用方法
peek()//返回队首元素
poll()//返回队首元素,队首元素出队列
add()//添加元素
size()//返回队列元素个数
isEmpty()//判断队列是否为空,为空返回true,不空返回false
❹栈-Stack/Deque
栈是一种后进先出的数据结构,元素从顶端入栈,然后从顶端出栈。
注意:Java 堆栈 Stack 类已经过时,Java 官方推荐使用 Deque 替代 Stack 使用。Deque 堆栈操作方法:push()、pop()、peek()。
创建栈
//方法一,弃用
Stack<E> stack=new Stack<>();
Stack<String> stack=new Stack<>();
//方法二:推荐使用
//底层:ArrayDeque(动态数组)和 LinkedList(链表)
Deque stack = new ArrayDeque<String>();
Deque stack = new LinkedList<String>();
stack.push("a");
stack.pop();
stack.push("b");
System.out.println(stack);
常用方法
| 函数 | 功能 |
|---|---|
| push(T t) | 压栈(向栈顶放入元素) |
| pop() | 出栈(拿出栈顶元素,并得到它的值) |
| peek() | 将栈顶元素返回,但是不从栈中移除它 |
| search(Object o) | 返回对象在此堆栈上的从1开始的位置。 |
| isEmpty() | 判断栈是否为空 |
| size() | 获取栈长度 |
❺堆-Heap
堆通常可以被看做是一棵完全二叉树的数组对象。
堆的特性:
- 1.堆是完全二叉树,除了树的最后一层结点不需要是满的,其它的每一层从左到右都是满的,如果最后一层结点不是满的,那么要求左满右不满。
- 2.堆通常用数组来实现。将二叉树的结点按照层级顺序放入数组中,根结点在位置1,它的子结点在位置2和3,而子结点的子结点则分别在位置4,5,6和7,以此类推。(0被废弃)
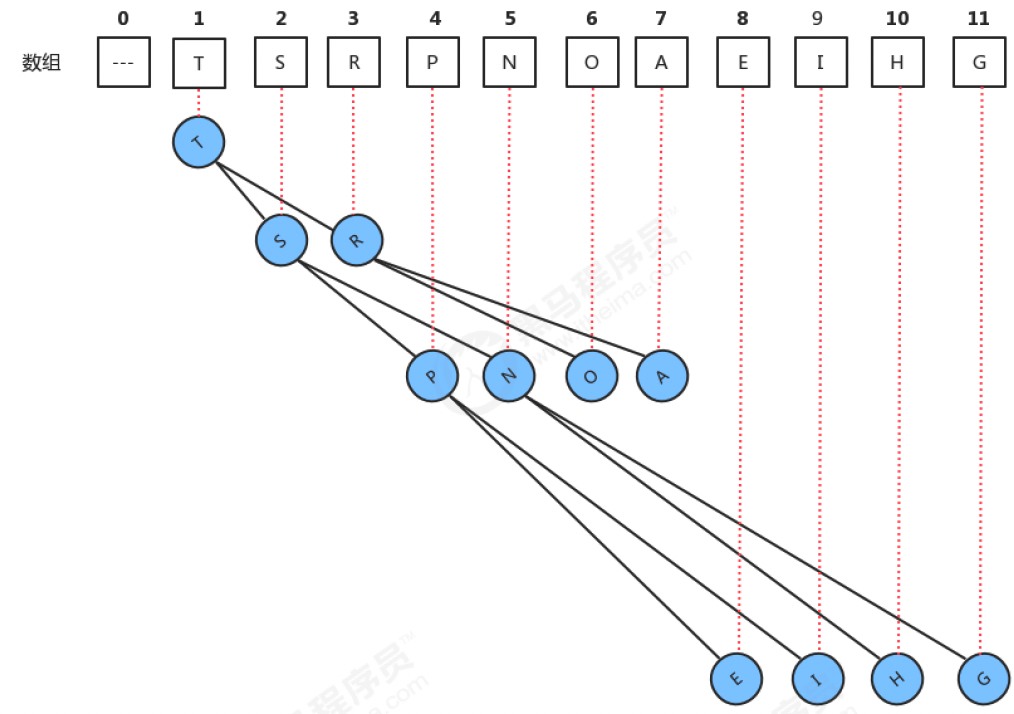
如果一个结点的位置为k,则它的父结点的位置为[k/2],而它的两个子结点的位置则分别为2k和2k+1。
这样,在不使用指针的情况下,我们也可以通过计算数组的索引在树中上下移动:从a[k]向上一层,就令k等于k/2,向下一层就令k等于2k或2k+1。
- 3.每个结点都大于等于它的两个子结点。这里要注意堆中仅仅规定了每个结点大于等于它的两个子结点,但这两个子结点的顺序并没有做规定,跟我们之前学习的二叉查找树是有区别的。
堆的API设计

public class Heap<T extends Comparable<T>> {
//存储堆中的元素
private T[] items;
//记录堆中元素的个数
private int N;
public Heap(int capacity) {
this.items = (T[]) new Comparable[capacity + 1];
this.N = 0;
}
//判断堆中索引i处的元素是否小于索引j处的元素
private boolean less(int i, int j) {
return items[i].compareTo(items[j]) < 0;
}
//交换堆中i索引和j索引处的值
private void exch(int i, int j) {
T temp = items[i];
items[i] = items[j];
items[j] = temp;
}
//往堆中插入一个元素
public void insert(T t) {
items[++N] = t;
swim(N);
}
//使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置
private void swim(int k) {
//通过循环,不断的比较当前结点的值和其父结点的值,如果发现父结点的值比当前结点的值小,则交换位置
while (k > 1) {
//比较当前结点和其父结点
if (less(k / 2, k)) {
exch(k / 2, k);
}
k = k / 2;
}
}
//删除堆中最大的元素,并返回这个最大元素
public T delMax() {
T max = items[1];
//交换索引1处的元素和最大索引处的元素,让完全二叉树中最右侧的元素变为临时根结点
exch(1, N);
//最大索引处的元素删除掉
items[N] = null;
//元素个数-1
N--;
//通过下沉调整堆,让堆重新有序
sink(1);
return max;
}
//使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k) {
//循环对比k结点和其左子结点2k以及右子结点2k+1处中的较大值的元素大小,如果当前结点小,则需要交换位置
while (2 * k <= N) {
//获取当前结点的子结点中的较大结点
int max;//记录较大结点所在的索引
if (2 * k + 1 <= N) {
if (less(2 * k, 2 * k + 1)) {
max = 2 * k + 1;
} else {
max = 2 * k;
}
} else {
max = 2 * k;
}
//比较当前结点和较大结点的值
if (!less(k, max)) {
break;
}
//交换k索引处的值和max索引处的值
exch(k, max);
//变换k的值
k = max;
}
}
public static void main(String[] args) {
Heap<String> heap = new Heap<String>(20);
heap.insert("A");
heap.insert("B");
heap.insert("C");
heap.insert("D");
heap.insert("E");
heap.insert("F");
heap.insert("G");
String del;
//循环删除
while ((del = heap.delMax()) != null) {
System.out.print(del + ",");
}
}
}
④哈希表
❶基础知识
哈希表(Hash table),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做哈希表。
常见的三种哈希结构
- 数组
int[] hashTable = new int[26]; //存26字母索引
//hashTable[s.charAt(i) - 'a']++; 字母存在则在对应位置加1
- set (集合)
Set<Integer> set = new HashSet<>();
//set.add(num) 插入元素
//set.contains(num) 查找键是否存在
- map(映射)
Map<Integer, Integer> map = new HashMap<>();
//map.put(key,value) 插入元素
//map.getOrDefault(ch, 0); 查询map是否存在ch,不存在设置默认值0
//map.values() 返回所有value
//map.containsKey(key) 查找键是否存在
//map.isEmpty() 判断是否为空
//map.get() 根据键获取值
//map.remove() 根据键删除映射关系
⑤字符串
双指针:344. 反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
示例 1:
输入:s = ["h","e","l","l","o"]
输出:["o","l","l","e","h"]
示例 2:
输入:s = ["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"]
class Solution {
public void reverseString(char[] s) {
int left = 0, right = s.length - 1;
while(left < right){
char tmp = s[left];
s[left] = s[right];
s[right] = tmp;
left++;
right--;
}
}
class Solution {
public void reverseString(char[] s) {
int n = s.length;
for (int left = 0, right = n - 1; left < right; ++left, --right) {
char tmp = s[left];
s[left] = s[right];
s[right] = tmp;
}
}
}
class Solution {
public void reverseString(char[] s) {
int l = 0;
int r = s.length - 1;
while (l < r) {
s[l] ^= s[r]; //构造 a ^ b 的结果,并放在 a 中
s[r] ^= s[l]; //将 a ^ b 这一结果再 ^ b ,存入b中,此时 b = a, a = a ^ b
s[l] ^= s[r]; //a ^ b 的结果再 ^ a ,存入 a 中,此时 b = a, a = b 完成交换
l++;
r--;
}
}
}
双指针: 541. 反转字符串 II
给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
- 如果剩余字符少于
k个,则将剩余字符全部反转。 - 如果剩余字符小于
2k但大于或等于k个,则反转前k个字符,其余字符保持原样。
示例 1:
输入:s = "abcdefg", k = 2
输出:"bacdfeg"
示例 2:
输入:s = "abcd", k = 2
输出:"bacd"
题意:每隔2k个反转前k个,尾数不够k个时候全部反转
class Solution {
public String reverseStr(String s, int k) {
int n = s.length();
char[] arr = s.toCharArray();
// 1. 每隔 2k 个字符的前 k 个字符进行反转
for (int i = 0; i < n; i += 2 * k) {
// 2. 剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符
if (i + k <= n) {
reverse(arr, i, i + k - 1);
continue;
}
// 3. 剩余字符少于 k 个,则将剩余字符全部反转
reverse(arr, i, n - 1);
}
return new String(arr);
}
// 定义翻转函数
public void reverse(char[] arr, int left, int right) {
while (left < right) {
char temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
left++;
right--;
}
}
}
class Solution {
public String reverseStr(String s, int k) {
int n = s.length();
char[] arr = s.toCharArray();
for (int i = 0; i < n; i += 2 * k) {
// 1. 每隔 2k 个字符的前 k 个字符进行反转
// 2. 剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符
reverse(arr, i, Math.min(i + k, n) - 1);
}
return String.valueOf(arr);
}
public void reverse(char[] arr, int left, int right) {
while (left < right) {
char temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
left++;
right--;
}
}
}
双指针:345. 反转字符串中的元音字母
给你一个字符串 s ,仅反转字符串中的所有元音字母,并返回结果字符串。
元音字母包括 'a'、'e'、'i'、'o'、'u',且可能以大小写两种形式出现不止一次。
示例 1:
输入:s = "hello"
输出:"holle"
示例 2:
输入:s = "leetcode"
输出:"leotcede"
class Solution {
public String reverseVowels(String s) {
//定义两个哨兵
int l = 0, r = s.length() - 1;
char[] arr = s.toCharArray();
while (l < r) {
//从左往右找元音字母,找到就停止,没找到就继续右移
while (!"aeiouAEIOU".contains(String.valueOf(arr[l])) && l < r) l++;
//从右往左找元音字母,找到就停止,没找到就继续左移
while (!"aeiouAEIOU".contains(String.valueOf(arr[r])) && l < r) r--;
//两边都找到就交换它们
if (l < r) {
char temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
l++;
r--;
}
}
return new String(arr);
}
}
双指针:1768. 交替合并字符串
给你两个字符串 word1 和 word2 。请你从 word1 开始,通过交替添加字母来合并字符串。如果一个字符串比另一个字符串长,就将多出来的字母追加到合并后字符串的末尾。
返回 合并后的字符串 。
示例 1:
输入:word1 = "abc", word2 = "pqr"
输出:"apbqcr"
解释:字符串合并情况如下所示:
word1: a b c
word2: p q r
合并后: a p b q c r
示例 2:
输入:word1 = "ab", word2 = "pqrs"
输出:"apbqrs"
解释:注意,word2 比 word1 长,"rs" 需要追加到合并后字符串的末尾。
word1: a b
word2: p q r s
合并后: a p b q r s
示例 3:
输入:word1 = "abcd", word2 = "pq"
输出:"apbqcd"
解释:注意,word1 比 word2 长,"cd" 需要追加到合并后字符串的末尾。
word1: a b c d
word2: p q
合并后: a p b q c d
class Solution {
public String mergeAlternately(String word1, String word2) {
StringBuilder sb = new StringBuilder();
int m = word1.length(), n = word2.length();
int i = 0, j = 0;
while(i < m && j < n){
sb.append(word1.charAt(i));
sb.append(word2.charAt(j));
i++;
j++;
}
while(i < m){
sb.append(word1.charAt(i));
i++;
}
while(j < n){
sb.append(word2.charAt(j));
j++;
}
return sb.toString();
}
}
class Solution {
public String mergeAlternately(String word1, String word2) {
StringBuilder sb = new StringBuilder();
int m = word1.length(), n = word2.length();
int i = 0, j = 0;
while(i < m || j < n){
if(i < m){
sb.append(word1.charAt(i));
i++;
}
if(j < n){
sb.append(word2.charAt(j));
j++;
}
}
return sb.toString();
}
}
⑥双指针
344. 反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
示例 1:
输入:s = ["h","e","l","l","o"]
输出:["o","l","l","e","h"]
示例 2:
输入:s = ["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"]
class Solution {
public void reverseString(char[] s) {
int left = 0, right = s.length - 1;
while(left < right){
char tmp = s[left];
s[left] = s[right];
s[right] = tmp;
left++;
right--;
}
}
class Solution {
public void reverseString(char[] s) {
int n = s.length;
for (int left = 0, right = n - 1; left < right; ++left, --right) {
char tmp = s[left];
s[left] = s[right];
s[right] = tmp;
}
}
}
class Solution {
public void reverseString(char[] s) {
int l = 0;
int r = s.length - 1;
while (l < r) {
s[l] ^= s[r]; //构造 a ^ b 的结果,并放在 a 中
s[r] ^= s[l]; //将 a ^ b 这一结果再 ^ b ,存入b中,此时 b = a, a = a ^ b
s[l] ^= s[r]; //a ^ b 的结果再 ^ a ,存入 a 中,此时 b = a, a = b 完成交换
l++;
r--;
}
}
}
27. 移除元素
给你一个数组 nums 和一个值 val,你需要原地移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
//双指针
class Solution {
public int removeElement(int[] nums, int val) {
//快慢指针解法
int slow = 0; //慢指针
//快指针,无论与val值是否相同每遍历一次都要移动一位
for(int fast = 0; fast < nums.length; fast++){
//快指针先走,判断快指针指向的元素是否等于val
if(nums[fast] != val){
nums[slow] = nums[fast];
slow++; //只有当快指针不等于val的时候,慢指针才和快指针一起移动一位
}
}
return slow;
}
}
//通用解法
class Solution {
public int removeElement(int[] nums, int val) {
int idx = 0;
for (int x : nums) {
if (x != val) nums[idx++] = x;
}
return idx;
}
}
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
class Solution {
public void moveZeroes(int[] nums) {
// 去除 nums 中的所有 0
// 返回去除 0 之后的数组长度
int p = removeElement(nums, 0);
// 将 p 之后的所有元素赋值为 0
for (; p < nums.length; p++) {
nums[p] = 0;
}
}
// 双指针技巧,复用 [27. 移除元素] 的解法。
int removeElement(int[] nums, int val) {
int fast = 0, slow = 0;
while (fast < nums.length) {
if (nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
}
fast++;
}
return slow;
}
}
快排思想,用 0 当做这个中间点,把不等于 0的放到中间点的左边,等于 0 的放到其右边。使用两个指针 i 和 j,只要 nums[i]!=0,我们就交换 nums[i] 和 nums[j]
class Solution {
public void moveZeroes(int[] nums) {
if(nums == null) return;
//两个指针i和j
int j = 0;
for(int i = 0; i < nums.length; i++) {
//当前元素!=0,就把其交换到左边,等于0的交换到右边
if(nums[i] != 0) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j++] = tmp;
}
}
}
}
⑦二叉树
二叉树基础知识
- 二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分
- 二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个节点
//Definition for a binary tree node.
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
我们有一棵二叉树:
根
/ \
左 右
栈是一种 先进后出的结构,那么入栈顺序必须调整为倒序
- 前序遍历,出栈顺序:根左右; 入栈顺序:右左根
- 中序遍历,出栈顺序:左根右; 入栈顺序:右根左
- 后序遍历,出栈顺序:左右根; 入栈顺序:根右左
❶二叉树遍历
144. 二叉树的前序遍历
先输出父节点,再遍历左子树和右子树
1.递归
/**
*时间:O(n)
*空间:O(h)
**/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
dfs(root, res);
return res;
}
public void dfs(TreeNode root, List<Integer> res){
if(root == null){
return;
}
res.add(root.val);
dfs(root.left, res);
dfs(root.right, res);
}
}
2.迭代
- 弹栈顶入列表
- 如有右,先入右
- 如有左,再入左
/**
*时间:O(n)
*空间:O(h)
**/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if(root == null) {
return res;
}
Deque<TreeNode> stack = new LinkedList<>();// 用栈来实现迭代
stack.push(root);
while(!stack.isEmpty()){
TreeNode tmp = stack.pop();
res.add(tmp.val);
if(tmp.right != null){ //先进右节点,后出
stack.push(tmp.right);
}
if(tmp.left != null){ //后进左节点,先出
stack.push(tmp.left);
}
}
return res;
}
}
94. 二叉树的中序遍历
先遍历左子树,再输出父节点,再遍历右子树
1.递归
/**
*时间:O(n)
*空间:O(h)
**/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
dfs(root, res);
return res;
}
public void dfs(TreeNode root, List<Integer> res){
if(root == null){
return;
}
dfs(root.left, res);
res.add(root.val);
dfs(root.right, res);
}
}
2.迭代
- 根结点不为空,入栈并向左走。整条界依次入栈
- 根结点为空,弹栈顶打印,向右走。
/**
*时间:O(n)
*空间:O(h)
**/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
Deque<TreeNode> stack = new LinkedList<>();
while (root != null || !stack.isEmpty()) {
while (root != null) { // 将根和左子树入栈
stack.push(root);
root = root.left;
}
//当前节点为空,说明左边走到头了,从栈中弹出节点并保存
TreeNode tmp = stack.pop();
res.add(tmp.val);
//然后转向右边节点,继续上面整个过程
root = tmp.right;
}
return res;
}
}
/**
*时间:O(n)
*空间:O(h)
**/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
Deque<TreeNode> stack = new LinkedList<>();
while (root != null || !stack.isEmpty()) {
if (root != null) {
stack.push(root);
root = root.left;
} else {
TreeNode tmp = stack.pop();
res.add(tmp.val);
root = tmp.right;
}
}
return res;
}
}
145. 二叉树的后序遍历
先遍历左子树,再遍历右子树,最后输出父节点
1.递归
/**
*时间:O(n)
*空间:O(h)
**/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
dfs(root, res);
return res;
}
public void dfs(TreeNode root ,List<Integer> res){
if(root == null){
return;
}
dfs(root.left, res);
dfs(root.right, res);
res.add(root.val);
}
}
2.迭代
- 弹栈顶输出
- 如有左,压入左
- 如有右,压入右
/**
*时间:O(n)
*空间:O(h)
**/
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) {
return res;
}
Deque<TreeNode> stack = new LinkedList<>();
TreeNode prev = null;
while (!stack.isEmpty() || root != null) {
while (root != null) { // 将左子树全部入栈
stack.push(root);
root = root.left;
}
root = stack.pop(); // 拿取栈顶节点
if (root.right == null || root.right == prev) {
res.add(root.val);
prev = root;
root = null;
} else {
// 重新把根节点入栈,处理完右子树还要回来处理根节点
stack.push(root);
// 当前节点为右子树
root = root.right;
}
}
return res;
}
}
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> stack = new LinkedList<>();
if(root == null){
return res;
}
// 如果当前处理节点不为空或者栈中有数据则继续处理
stack.push(root);
while (!stack.isEmpty()) {
TreeNode tmp = stack.pop();
res.add(tmp.val);
if(tmp.left != null) stack.push(tmp.left);
if(tmp.right != null) stack.push(tmp.right); //出栈根右左
}
Collections.reverse(res);//反转之后:左右根
return res;
}
}
102. 二叉树的层序遍历
1.递归
/**
*时间:O(n)
*空间:O(h)
**/
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
dfs(root, 0, res);
return res;
}
public void dfs(TreeNode root, Integer level, List<List<Integer>> res) {
if (root == null) return;
if (res.size() <= level) {
//如果res.size() <= level说明下一层的集合还没创建,所以要先创建下一层的集合
List<Integer> item = new ArrayList<Integer>();
res.add(item);
}
//遍历到第几层我们就操作第几层的数据
List<Integer> list = res.get(level);
list.add(root.val);
//分别遍历左右两个子节点,到下一层了,所以层数要加1
dfs(root.left, level + 1, res);
dfs(root.right, level + 1, res);
}
}
2.迭代
/**
*时间:O(n)
*空间:O(n)
**/
//借助队列
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
if (root == null) {
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
//Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> level = new ArrayList<Integer>();
int currentLevelSize = queue.size();
for (int i = 0; i < currentLevelSize; i++) {
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
res.add(level);
}
return res;
}
}
103. 二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
递归
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
dfs(root, 0, res);
return res;
}
public void dfs(TreeNode root, Integer level, List<List<Integer>> res) {
if (root == null) return;
if (res.size() <= level) {
//如果res.size() <= level说明下一层的集合还没创建,所以要先创建下一层的集合
List<Integer> item = new ArrayList<>();
res.add(item);
}
//遍历到第几层我们就操作第几层的数据
List<Integer> list = res.get(level);
if (level % 2 == 0){
list.add(root.val); //根节点是第0层,偶数层相当于从左往右遍历,所以要添加到集合的末尾
} else {
list.add(0, root.val); //如果是奇数层相当于从右往左遍历,要把数据添加到集合的开头
}
//分别遍历左右两个子节点,到下一层了,所以层数要加1
dfs(root.left, level + 1, res);
dfs(root.right, level + 1, res);
}
}
迭代
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<List<Integer>>();
if(root == null){
return res;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
boolean flag = true; // 为 true 时从左开始,false 时从右开始,第一步先从左边开始打印
while(!queue.isEmpty()){
List<Integer> list = new ArrayList<>();
int n = queue.size();
for(int i = 0; i < n; i++){
TreeNode node = queue.poll();
if (flag){
list.add(node.val);
} else {
list.add(0, node.val);
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
flag = !flag; // 切换方向
res.add(list);
}
return res;
}
}
⑧图
图这种数据结构有一些比较特殊的算法,比如二分图判断,有环图无环图的判断,拓扑排序,以及最经典的最小生成树,单源最短路径问题,更难的就是类似网络流这样的问题。
参考:图论基础及遍历算法、二分图判定算法、环检测和拓扑排序、图遍历算法、名流问题、并查集算法计算连通分量、Dijkstra 最短路径算法
图论基础
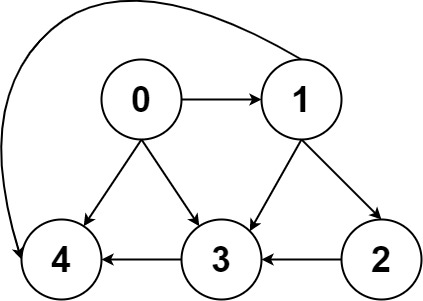
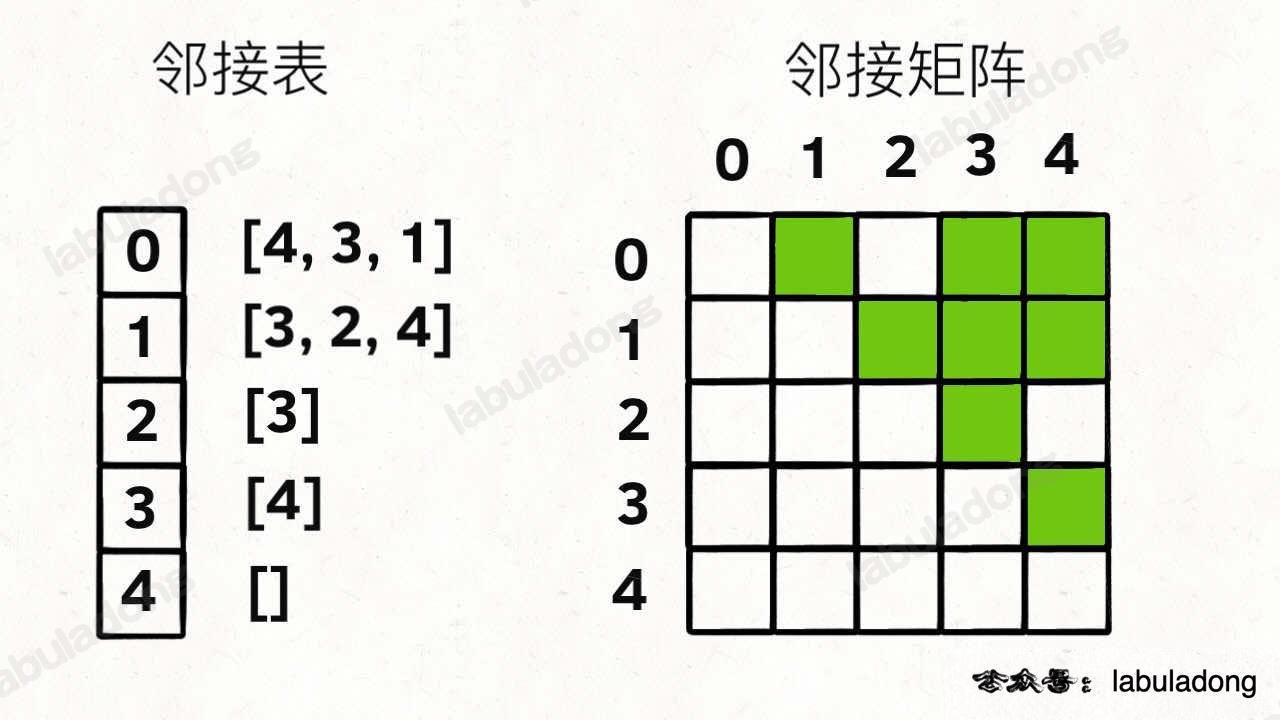
「图」的两种表示方法,邻接表(链表),邻接矩阵(二维数组)。
邻接矩阵判断连通性迅速,并可以进行矩阵运算解决一些问题,但是如果图比较稀疏的话很耗费空间。
邻接表比较节省空间,但是很多操作的效率上肯定比不过邻接矩阵。
 |
 |
|---|---|
邻接表把每个节点 x 的邻居都存到一个列表里,然后把 x 和这个列表关联起来,这样就可以通过一个节点 x 找到它的所有相邻节点。
邻接矩阵则是一个二维布尔数组,我们权且称为 matrix,如果节点 x 和 y 是相连的,那么就把 matrix[x][y] 设为 true(上图中绿色的方格代表 true)。如果想找节点 x 的邻居,去扫一圈 matrix[x][..] 就行了。
如果用代码的形式来表现,邻接表和邻接矩阵大概长这样:
// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;
// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;
邻接表建立
//把图转化成邻接表
List<Integer>[] buildGraph(int x, int[][] edges) {
// 图中共有 x 个节点
List<Integer>[] graph = new LinkedList[x];
for (int i = 0; i < x; i++) {
graph[i] = new LinkedList<>();
}
// edges = [[1,0],[0,1]]
for (int[] edge : edges) {
// from = 0, to = 1
int from = edge[1], to = edge[0];
// 添加一条从 from 指向 to 的有向边
graph[from].add(to);
}
return graph;
}
图遍历
图和多叉树最大的区别是,图是可能包含环的,你从图的某一个节点开始遍历,有可能走了一圈又回到这个节点,而树不会出现这种情况,从某个节点出发必然走到叶子节点,绝不可能回到它自身。
所以,如果图包含环,遍历框架就要一个 visited 数组进行辅助:
// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;
/* 图遍历框架 */
void traverse(Graph graph, int s) {
if (visited[s]) return; // 已被遍历
// 经过节点 s,标记为已遍历
visited[s] = true;
// 做选择:标记节点 s 在路径上
onPath[s] = true;
for (int neighbor : graph[s] {
traverse(graph, neighbor);
}
// 撤销选择:节点 s 离开路径
onPath[s] = false;
}
环检测
类比贪吃蛇游戏,visited 记录蛇经过过的格子,而 onPath 仅仅记录蛇身。onPath 用于判断是否成环,类比当贪吃蛇自己咬到自己(成环)的场景。
// 记录一次递归路径中的节点
boolean[] onPath;
// 记录遍历过的节点,防止走回头路
boolean[] visited;
// 记录图中是否有环
boolean hasCycle = false;
void traverse(List<Integer>[] graph, int s) {
// 出现环
if (onPath[s]) {
hasCycle = true;
}
// 如果已经找到了环,也不用再遍历了
if (visited[s] || hasCycle) {
return;
}
// 前序代码位置
visited[s] = true; // 将当前节点标记为已遍历
onPath[s] = true; // 开始遍历节点 s
for (int neighbor : graph[s]) {
traverse(graph, neighbor);
}
// 后序代码位置
onPath[s] = false; // 节点 s 遍历完成
}






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 三行代码完成国际化适配,妙~啊~
· .NET Core 中如何实现缓存的预热?