归并排序分析
一.归并排序原理
1.拆分(以二分归并排序为例:将一个数组折半拆分为两个数组,直到不可拆分)
2.比较(元素之间两两进行比较)
3.归并(元素比较完成后进行合并)
用百度百科的一张图更加方便地理解:
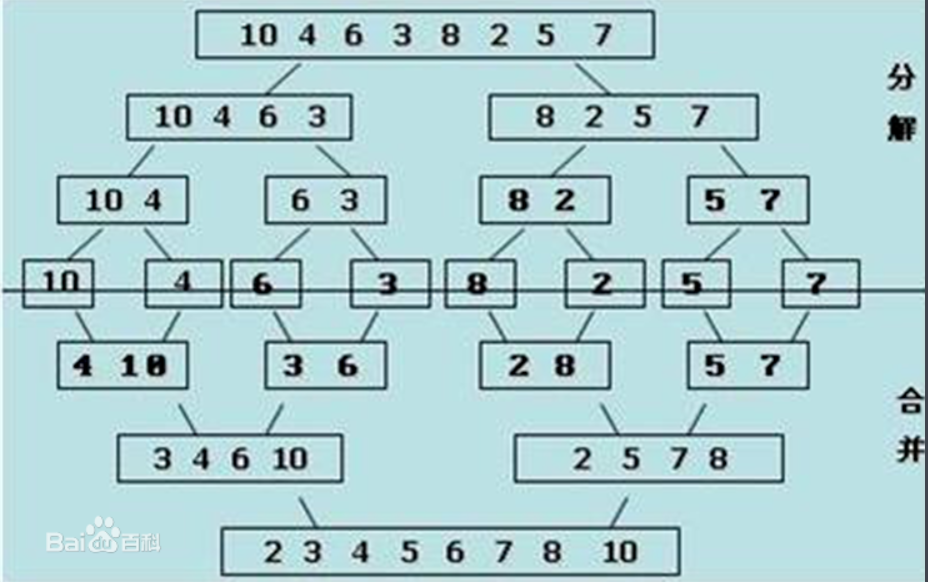
归并排序是一种稳定的排序算法,但是用到了递归,比较消耗内存。
二.归并排序时间复杂度分析
归并排序的时间复杂度包括分解,比较,合并。
最好的情况下,数组是已排序的,那么归并排序的时间复杂度为O(n)级的。
最坏的情况下,数组是逆序的,那么归并排序的时间复杂度为O(nlogn)级的。归并排序的平均时间复杂度是O(nlogn)。
三.代码实现(Java)
package json.study; import java.util.Arrays; public class Test05 { static int number=0; public static void main(String[] args) { int[] arr = {9,8,7,5,6,1,2,3,4}; cutAndSort(arr); System.out.println(Arrays.toString(arr)); } private static void cutAndSort(int[] arr) { cutAndSort(arr, 0, arr.length - 1); } private static void cutAndSort(int[] arr, int left, int right) {//方法重载,用递归方法折半拆分数组并排序 //如果数组只有一个元素则直接退出,否则 if(left==right) return; int mid = (left + right) / 2; cutAndSort(arr, left, mid);//左边排好序后的数组 cutAndSort(arr, mid + 1, right);//右边排好序后的数组 merge(arr, left, mid, right); } private static void merge(int[] arr, int left, int mid, int right) { int[] tmp = new int[arr.length]; int rIndex = mid + 1; int tIndex = left; int cIndex = left; while(left <=mid && rIndex <= right) { if (arr[left] <= arr[rIndex]) tmp[tIndex++] = arr[left++]; else tmp[tIndex++] = arr[rIndex++]; } // 将左边剩余的归并 while (left <=mid) { tmp[tIndex++] = arr[left++]; } // 将右边剩余的归并 while (rIndex <= right) { tmp[tIndex++] = arr[rIndex++]; } while(cIndex<=right){ arr[cIndex]=tmp[cIndex]; cIndex++; } } }
测试结果如下:
![]()

