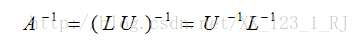LU分解求逆

文章转自：

https://www.cnblogs.com/bigmonkey/p/9555710.html

https://blog.csdn.net/xx_123_1_rj/article/details/39553809

什么是LU分解

在线性代数中， LU分解是矩阵分解的一种，可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积（有时是它们和一个置换矩阵的乘积）

如果有一个矩阵A，将A表示成下三角矩阵L和上三角矩阵U的乘积，称为A的LU分解。

 

　　更进一步，我们希望下三角矩阵的对角元素都为1：

LU分解的步骤

　　上一章讲到，对于满秩矩阵A来说，通过左乘一个消元矩阵，可以得到一个上三角矩阵U。

　　可以看到，L实际上就是消元矩阵的逆。容易知道二阶矩阵的逆：

 

　　现在假设A是一个3×3矩阵，在不考虑行交换的情况下，通过消元得到上三角矩阵的过程是：

 

 

LU 分解的前提

　　并非所有矩阵都能进行LU分解，能够LU分解的矩阵需要满足以下三个条件：

1. 矩阵是方阵（LU分解主要是针对方阵）；
2. 矩阵是可逆的，也就是该矩阵是满秩矩阵，每一行都是独立向量；
3. 消元过程中没有0主元出现，也就是消元过程中不能出现行交换的初等变换

 示例

　　

　　如果A存在LU分解存，a,b满足什么条件？

　　使用消元法逐一消去主元：

　　由于E₃₁ 中出现了 –b/a，所以a ≠ 0

 

　　b可以是任意常数。

 

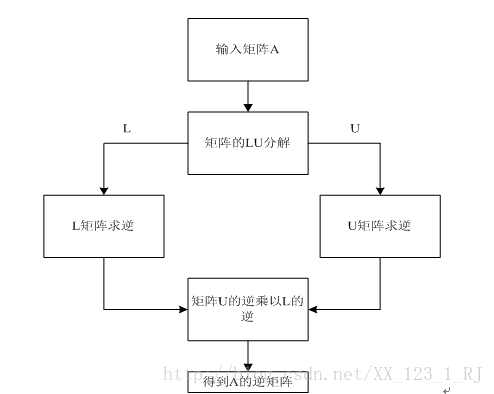
具体的算法流程可以是：

 

1)进行LU分解；

2)对分解后的L阵（下三角矩阵）和U阵（上三角矩阵）进行求逆;

3)L阵的逆矩阵和U阵的逆矩阵相乘，即可求得原来矩阵的逆。即：

程序实现如下：

 

#include<stdio.h>
#include <string.h>
#define N 4
void main()
{ 
    float a[N][N];
    float L[N][N],U[N][N],out[N][N], out1[N][N];
    float r[N][N],u[N][N];
    memset( a , 0 , sizeof(a));  //初始化
    memset( L , 0 , sizeof(L));
    memset( U , 0 , sizeof(U));
    memset( r , 0 , sizeof(r));
    memset( u , 0 , sizeof(u));
    int n=N;
    int k,i,j;
    int flag=1;
    float s,t;
    ////////////////////input a matrix////
    printf("input A=\n");
    for(i=0;i<n;i++)
        for(j=0;j<n;j++)
            scanf("%f",&a[i][j]);
        //////////////////figure the input matrix//////////////////////////
        printf("输入矩阵:\n");
        for(i=0;i<n;i++)
        {
            for (j = 0; j < n; j++)
            {
                printf("%lf ", a[i][j]);
            }
            printf("\n");
        }
        for(j=0;j<n;j++)
            a[0][j]=a[0][j];  //计算U矩阵的第一行
        
        for(i=1;i<n;i++)
            a[i][0]=a[i][0]/a[0][0];   //计算L矩阵的第1列
        for(k=1;k<n;k++)
        {
            for(j=k;j<n;j++)
            {
                s=0;
                for (i=0;i<k;i++)
                    s=s+a[k][i]*a[i][j];   //累加
                a[k][j]=a[k][j]-s; //计算U矩阵的其他元素
            }
            for(i=k+1;i<n;i++)
            {
                t=0;
                for(j=0;j<k;j++)
                    t=t+a[i][j]*a[j][k];   //累加
                a[i][k]=(a[i][k]-t)/a[k][k];    //计算L矩阵的其他元素
            }
        }
        for(i=0;i<n;i++)
            for(j=0;j<n;j++)
            { 
                if(i>j)
                { 
                    L[i][j]=a[i][j]; 
                    U[i][j]=0;
                }//如果i>j，说明行大于列，计算矩阵的下三角部分，得出L的值，U的//为0
                else
                {
                    U[i][j]=a[i][j];
                    if(i==j) 
                        L[i][j]=1;  //否则如果i<j，说明行小于列，计算矩阵的上三角部分，得出U的//值，L的为0
                    else 
                        L[i][j]=0;
                }
            }  
            if(U[1][1]*U[2][2]*U[3][3]*U[4][4]==0)
            {
                flag=0;
                printf("\n逆矩阵不存在");}
            if(flag==1)
            {
                /////////////////////求L和U矩阵的逆
                for (i=0;i<n;i++) /*求矩阵U的逆 */
                {
                    u[i][i]=1/U[i][i];//对角元素的值，直接取倒数
                    for (k=i-1;k>=0;k--)
                    {
                        s=0;
                        for (j=k+1;j<=i;j++)
                            s=s+U[k][j]*u[j][i];
                        u[k][i]=-s/U[k][k];//迭代计算，按列倒序依次得到每一个值，
                    }
                }
                for (i=0;i<n;i++) //求矩阵L的逆 
                {
                    r[i][i]=1; //对角元素的值，直接取倒数，这里为1
                    for (k=i+1;k<n;k++)
                    {
                        for (j=i;j<=k-1;j++)
                            r[k][i]=r[k][i]-L[k][j]*r[j][i];   //迭代计算，按列顺序依次得到每一个值
                    }
                }
                /////////////////绘制矩阵LU分解后的L和U矩阵///////////////////////
                printf("\nLU分解后L矩阵:");
                for(i=0;i<n;i++)
                { 
                    printf("\n");
                    for(j=0;j<n;j++)
                        printf(" %lf",L[i][j]);
                }
                printf("\nLU分解后U矩阵:");
                for(i=0;i<n;i++)
                { 
                    printf("\n");
                    for(j=0;j<n;j++)
                        printf(" %lf",U[i][j]);
                }
                printf("\n");
                ////////绘制L和U矩阵的逆矩阵
                printf("\nL矩阵的逆矩阵:");
                for(i=0;i<n;i++)
                { 
                    printf("\n");
                    for(j=0;j<n;j++)
                        printf(" %lf",r[i][j]);
                }
                printf("\nU矩阵的逆矩阵:");
                for(i=0;i<n;i++)
                { 
                    printf("\n");
                    for(j=0;j<n;j++)
                        printf(" %lf",u[i][j]);
                }
                printf("\n");
                //验证将L和U相乘，得到原矩阵
                printf("\nL矩阵和U矩阵乘积\n");
                for(i=0;i<n;i++)
                {
                    for(j=0;j<n;j++)
                    {
                        out[i][j]=0;
                    }
                }
                for(i=0;i<n;i++)
                {
                    for(j=0;j<n;j++)
                    {
                        for(k=0;k<n;k++)
                        {
                            out[i][j]+=L[i][k]*U[k][j];
                        }
                    }  
                }
                for(i=0;i<n;i++)
                {
                    for(j=0;j<n;j++)
                    {
                        printf("%lf\t",out[i][j]);
                    }
                    printf("\r\n");
                }
                //////////将r和u相乘，得到逆矩阵
                printf("\n原矩阵的逆矩阵:\n");
                for(i=0;i<n;i++)
                {
                    for(j=0;j<n;j++)
                    {out1[i][j]=0;}
                }
                for(i=0;i<n;i++)
                {
                    for(j=0;j<n;j++)
                    {
                        for(k=0;k<n;k++)            
                        {
                            out1[i][j]+=u[i][k]*r[k][j];
                        }
                    }  
                }
                for(i=0;i<n;i++)
                {
                    for(j=0;j<n;j++)
                    {
                        printf("%lf\t",out1[i][j]);
                    }
                    printf("\r\n");
                }
            }
 }