最小二乘法

宝宝问了我一个最小二乘法的算法，我忘记了，巩固了之后来总结一下。

首先先理解最小二乘法：

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

具体可以看链接：https://blog.csdn.net/ccnt_2012/article/details/81127117

最小二乘法的公式为：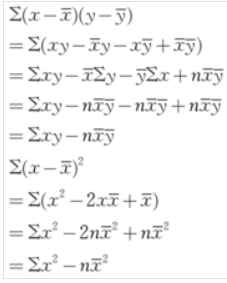

设拟合直线的公式为

  

,

其中：拟合直线的斜率为：

  

；计算出斜率后，根据

  

和已经确定的斜率k，利用待定系数法求出截距b。

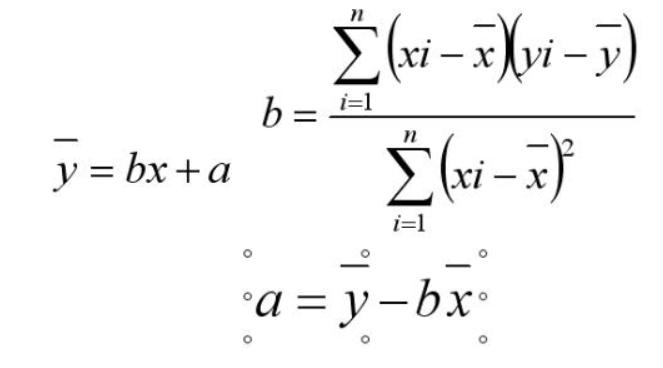
具体算法为：

①根据数据，就算出平均数X，和平均数Y，后面用大写的X和Y代表平均数
②计算（x1-X）×（y1-Y），计算（x2-X）×（y2-Y）……计算（xn-X）×（yn-Y）
③将②中计算得到的所有数据相加，作为分子
④计算（x1-X）²，计算（x2-X）²……计算（xn-X）²
⑤将④中计算得到的所有数据相加，作为分母
⑥将③中的分子和⑤中的分母相除，得到b
a用Y-bX计算。


例题：第一组
(9.84,7.72)
(7.38,8.00)
(4.92,8.13)
(2.46,8.30)
(0,8.51)
第二组
(7.18,7.90)
(5.38,7.96)
(3.52,8.16)
(1.75,8.38)
(0,8.51)     

用最小二乘法求拟合曲线的斜率
对这些点(x,y),直接用最小二乘法得出斜率及常数项：
y=bx+a .
b的分子为：(x1y1+x2y2+...xnyn)-nx'y' ,x',y'分别为xi,yi的平均值
b的分母为：(x1^2+x2^2+...xn^2)-n(x')^2 
求出了b之后,再用公式算出a=y'-bx'
对这两组,分别有：
y1=-0.0764x+8.508
y2=-0.0911x+8.507


代码为：

/// <summary>
    /// 最小二乘法线性拟合
    /// </summary>
    /// <param name="x">横坐标集合</param>
    /// <param name="y">纵坐标集合</param>
    /// <param name="slope">返回拟合直线的斜率</param>
    /// <param name="intercept">返回拟合直线的截距</param>
    /// <param name="r_square">返回相关系数R²</param>
    static void LinearFitting(double[] x, double[] y, out double slope, out double intercept, out double r_square)
    {
        int length = x.Length;
        double xmean = 0.0;
        double ymean = 0.0;
        for (int i = 0; i < length; i++)
        {
            xmean += x[i];
            ymean += y[i];
        }
        xmean /= length;
        ymean /= length;

        double sumx2 = 0.0;
        double sumy2 = 0.0;
        double sumxy = 0.0;
        for (int i = 0; i < length; i++)
        {
            sumx2 += (x[i] - xmean) * (x[i] - xmean);
            sumy2 += (y[i] - ymean) * (y[i] - ymean);
            sumxy += (y[i] - ymean) * (x[i] - xmean);
        }
        slope = sumxy / sumx2;
        intercept = ymean - slope * xmean;
        r_square = sumxy * sumxy / (sumx2 * sumy2);
　　　}

具体请看链接：https://www.cnblogs.com/Luohys/p/7459073.html