论文阅读--LEMNA: Explaining Deep Learning based Security Applications

摘要：

在视觉和NLP领域的可解释性方法在安全领域不适用，会造成严重的错误理解和解释错误。提出LEMNA->使用可解释模型解释复杂网络的局部，可用于验证模型表现，排除分类错误，并自动修补目标模型的错误。

1.引言：

1）深度学习广泛应用于恶意代码分类、二进制逆向工程、网络侵入检测，且精度很高。

2）但深度学习的缺乏透明度。已有的可解释性方法（视觉、NLP）只能提供形式化的解释，并不精确且保真度不够，应用到安全领域会造成错误理解和解释错误。

3）本文方法：给定输入数据x和黑箱分类器（e.g. RNN）,通过生成分类器在x附近的决策边界的局部近似来识别出对x有关键贡献的少量特征。

和以前的方法主要是假设不同，之前：假设局部近似是线性模型且特征相互独立   本文：保留局部非线性和特征依赖：1）混合的回归模型（喂入足够数据理论上可解释任何线性和非线性模型）;2）通过在学习过程中加入熔融lasso，混合回归模型可以将特征作为一个整体，从而捕获相邻特征之间的依赖关系；具有高保真度。

LEMNA 1)可以解释分类器的决策行为；2）可以从分类其中提取新的知识；3）解释分类器的错误（分析人员可以通过为每个可解释的错误增加训练样本来自动生成目标补丁，并通过目标再训练来提高分类器的性能）

2.可解释的机器学习

可解释的学习:网络学习完成后，便可直接获得特征的重要性衡量。e.g.线性模型

白盒可解释方法（模型架构、参数和训练数据都是已知的） :

　　1)基于输入或结构遮挡的正向传播: 扰乱输入(或隐藏的网络层)并观察相应的变化(假定扰动重要的特征更有可能导致网络结构和分类输出的重大变化）

　　(2)基于梯度的反向传播。基于反向传播的方法利用深度神经网络的梯度来推断特征的重要性。

黑盒可解释方法（输入输出已知）：

　　LIME:给定输入x,扰动x获取x附近点的一系列输出，用一个线性模型去拟合这些数据（线性模型的权重即反映x的重要性）。（j假定特征独立，不适于解释RNN）

　　还有一些工作使用其他的线性模型（决策树）来逼近决策边界。

机器学习解释 v.s.特征选择方法（e.g. PCA、稀疏编码、卡方统计）：前者解释如何对x分类；后者是在训练前减少特征维数，不能解释如何做出决策。

3.解释安全应用

现有安全应用主要是用RNN or MLP处理。

本文方法旨在在黑盒设置下工作，并有效地支持流行的深度学习模型，如RNN、MLP和CNN。更重要的是，该方法需要实现更高的解释保真度来解释安全应用程序。

4.实验方法

混合回归模型：（PI-k表示给每一个线性模型赋予的权重）

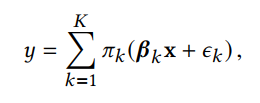
Fused Lasso (将分配给相邻特征的系数的不相似性限制在一个小阈值S内(即(超参数)当学习算法最小化损失函数时。因此，惩罚项迫使学习算法给相邻的特征分配相等的权重，这样可以让学习算法将特征看成组，挑选多个重要的特征组)（调整S的大小可以控制学习特征的依赖性大小）

　　

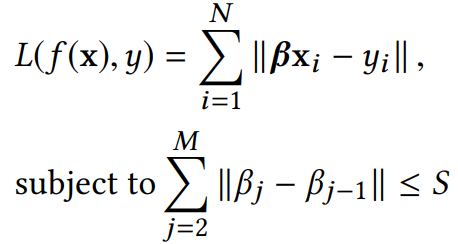
本文提出的模型(f表示混合回归模型）：

　　

 

 

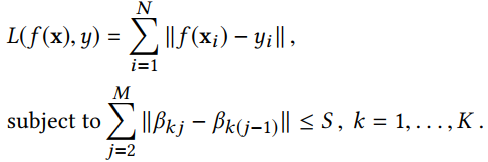
上图模型难于优化，本文提出了一个替代的方法-->用概率分布的形式表示混合回归模型： 

 

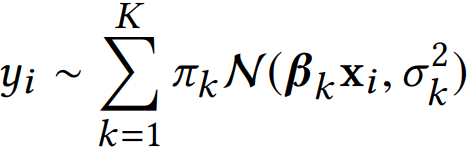
使用EM算法：

E:

M:

5. 评估

二进制逆向工程   pdf恶意检测

1.保真度评估(所选择的特征是否确实是分类结果的主要贡献者)：

 　　1）检验局部近似相对于原始决策边界的准确性;

　　　　  其中pi表示目标分类器分类为target的概率；pi-hat表示使用混合回归模型分类为target的概率。（这两个模型越接近，说明决策边界找的越和目标分类器一致）

　　  2) 对解释保真度进行端到端的评估(3种评估方法)

　　　　　a.若特征x对某类别是重要的，则删除x会导致误分类；

　　　　　b.若特征x对某类别是重要的，则在另一个类别样例中添加x会导致误分类；

　　　　　c.若特征x对某类别是重要的，则构造一个仅包含x的样例，也能将该样例分类到该类别。

2.实验结果

baseline: 1)LIME;2)随机特征选择方法

6.ML解释的应用

使用案例研究（二进制逆向工程）来说明解释结果如何帮助安全分析人员1)建立对经过训练的分类器的信任，2)排除分类错误，3)系统地修补目标错误

1)建立对经过训练的分类器的信任

　　a.捕获黄金法则（通过分析分类器，发现分类器发现了一些人类之前总结的法则）

　　b.发现新知识

2）故障诊断分类错误

　　深度神经网络高度精确，但其中的误差在实践中可能会被放大，不可简单忽视。

　　分别分析FN（false negative）和FP（false positive）的原因

3)系统地修补目标错误

　　识别分类其中训练不足的部分，扩充训练数据，修补特定错误。

　　e.g.给定分类错误实例，使用LEMNA查明致错的小功能集，通常情况下，这样的实例是训练数据中的异常值，并且没有足够的反例。为此，我们的策略是通过添加相关的反例来增加训练数据，用随机值代替Fx的特征值。

运用上述方法，重新训练模型，证明确实可以减少模型的误报率。

7.讨论

1.有利于解释 v.s. 可能被用于攻击模型

2.LEMNA对每一个样本输出一个解释，要彻底检查分类器的话，手工读取非常耗时。

　可先对相似的解释进行分组

3.特征可解释是，LEMNA是有用的。但是对于一些模糊特征（需训练模型时加入以增加模型对抗攻击的能力），LEMNA不适用

8.相关工作

本文提出的修补方法可以避免盲目对模型进行再训练  v.s. 提高模型的抗攻击能力是为了提高模型的鲁棒性。

一些研究探索了减少污染训练数据导致的错误分类的方法，e.g.标准的训练算法转化为求和形式来消除某些训练数据的影响;[29]提出利用一个影响函数来识别导致误分类的数据点。我们的方法是对现有工作的补充:我们建议增加培训数据来修复训练不足的组件(而不是删除糟糕的培训数据)。更重要的是，LEMNA帮助人类分析人员在打补丁之前理解这些错误。

 

p.s.

特征工程：在训练模型前选择特征的子集，降低学习问题的维度。

对抗学习：给定输入x，预测f(x)=y,希望发现一个最小的扰动使得f(x+delta) != f(x)。delta包含为改变预测需要修改那些特征的信息，而不是直接解释为什么模型对x的预测是f(x)。

可解释学习：为什么模型对x的预测是f(x)。