多项式回归模型

多项式回归模型

一、多项式拟合模型

1.1、概念

多项式拟合是一种通过将数据拟合到多项式函数来建立数学模型的方法。该方法可以用于分析实验或观测数据中的关系，并用多项式函数来逼近数据。在多项式拟合中，我们假设数据是由一个关于某些未知参数的多项式函数生成的，然后通过对数据进行最小二乘拟合来确定这些参数的值。最终得到的多项式函数可以用于预测新数据点的值或者分析数据中的趋势。

多项式拟合的一般形式如下：

\[y = a_0 + a_1x + a_2x^2 + ... + a_nx^n \]

其中，\(y\) 是响应变量，\(x\) 是解释变量，\(a_0, a_1, a_2, ..., a_n\) 是拟合参数。这个多项式函数可以是一次函数、二次函数、三次函数等等，具体的多项式阶数取决于数据的特点和需要拟合的程度。

多项式拟合可以用于拟合非线性数据，但是它也容易出现过拟合问题。在实际应用中，我们需要谨慎选择多项式的阶数，以避免过拟合和欠拟合的问题。通常，我们会使用交叉验证等技术来确定最优的多项式阶数，以获得更好的预测结果。

在使用多项式拟合模型时，通常需要进行以下几个步骤：

• 收集数据：收集需要分析的数据，并将其按照自变量的大小进行排序。

• 选择多项式次数：根据实际情况选择多项式的次数。如果选择的次数过小，模型可能会出现欠拟合；如果选择的次数过大，模型可能会出现过拟合。

• 拟合数据：将多项式方程与数据进行拟合，得到拟合的多项式曲线。

• 评估模型：通过一些指标如均方误差、确定系数等来评估拟合模型的好坏。

• 使用模型：利用拟合的模型对未知数据进行预测或者分析。

多项式拟合模型在实际应用中具有广泛的应用，例如在物理学、工程学、经济学等领域中常常用于建立数据与变量之间的关系，从而为决策提供依据。

1.2、实现代码

多项式拟合模型示例代码：

import numpy as np
import matplotlib.pyplot as plt

# 生成随机数据
x = np.linspace(0, 1, 100)
y = 2 * x**3 - 3 * x**2 + 1 + np.random.normal(0, 0.1, size=x.shape)

# 拟合多项式函数
p = np.polyfit(x, y, deg=3)
y_pred = np.polyval(p, x)

# 绘制拟合结果
plt.scatter(x, y, label='Data')
plt.plot(x, y_pred, color='r', label='Fit')
plt.legend()
plt.show()

输出：

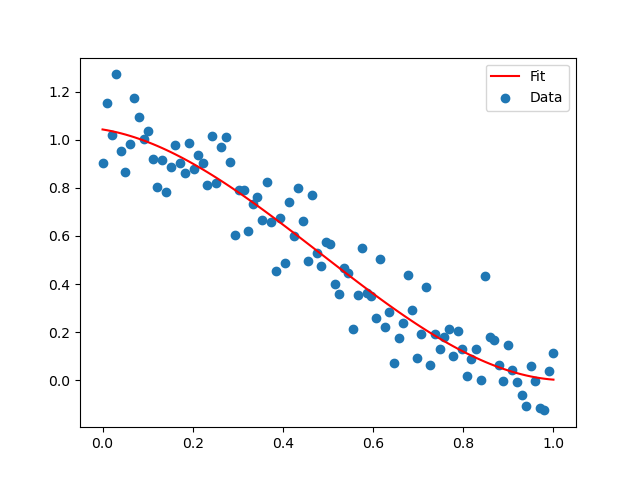
在这个示例中，多项式拟合模型使用了 numpy 库中的 polyfit 函数来拟合多项式函数。

1.3、应用代码

多项式拟合模型应用于股票预测示例代码：

import akshare as ak
import numpy as np
import matplotlib.pyplot as plt

# 获取股票历史数据
stock_data = ak.stock_zh_a_hist(symbol='000001', adjust="qfq").iloc[:, :6]
stock_data.columns = [
    'date', 'open', 'close', 'high', 'low', 'volume',
]
stock_price = stock_data['close'].values
dates = stock_data.index

# 定义多项式拟合模型
degree = 3  # 多项式阶数
x = np.arange(len(stock_price))
coeffs = np.polyfit(x, stock_price, degree)
polyfit = np.polyval(coeffs, x)

# 绘制原始数据和拟合曲线
plt.plot(dates, stock_price, 'o', label='Stock Price')
plt.plot(dates, polyfit, label='Polyfit')
plt.legend()
plt.show()

# 使用拟合模型预测未来5天的股票价格
future_days = 5
x_future = np.arange(len(stock_price), len(stock_price) + future_days)
polyfit_future = np.polyval(coeffs, x_future)

print("未来5天的预测股票价格：")
print(polyfit_future)

可视化：

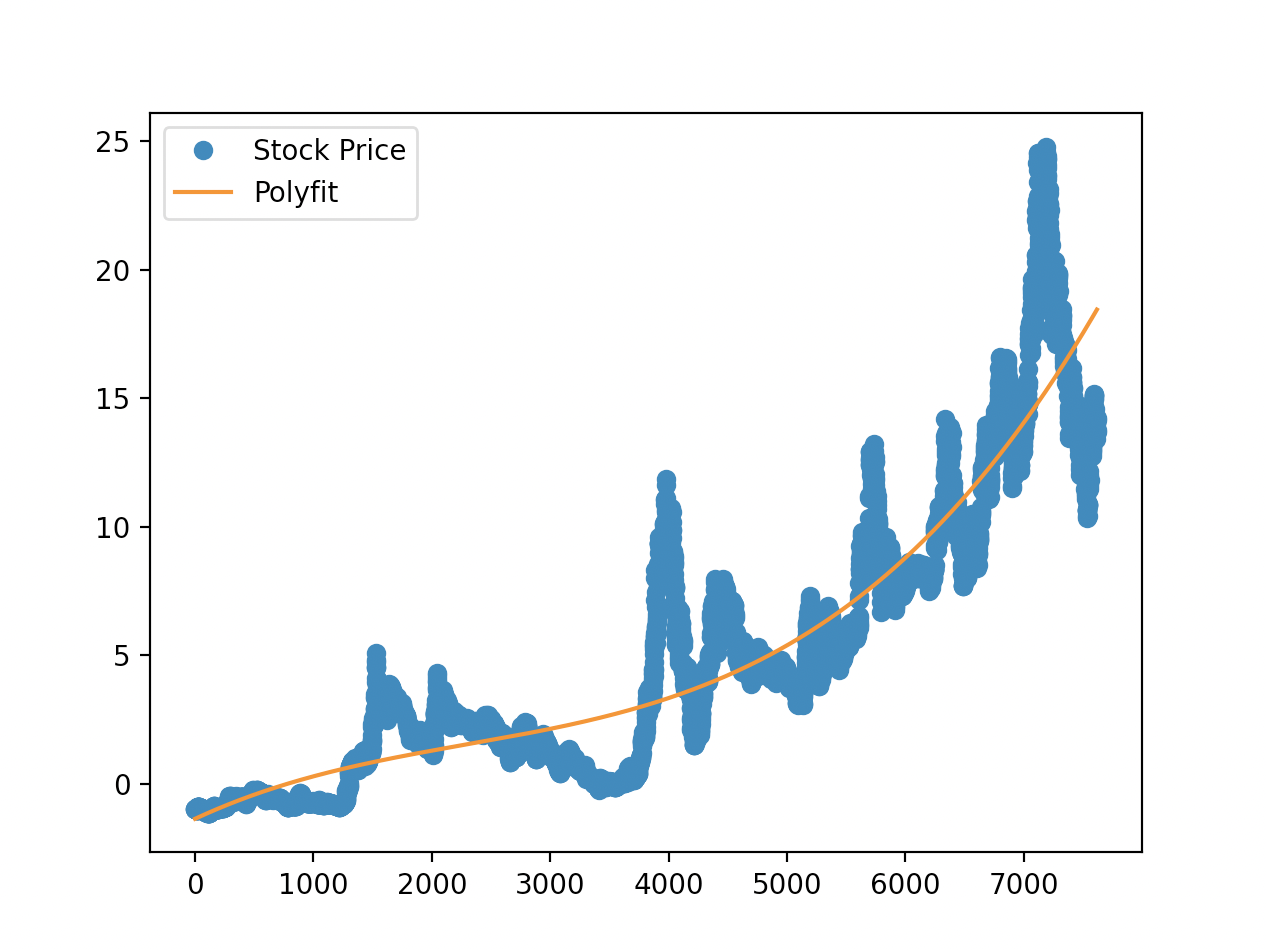
输出：

未来5天的预测股票价格：
[18.45748729 18.46539482 18.47330501 18.48121788 18.48913341]

上述代码，确定最优的的多项式阶数是关键，阶数过大导致过拟合，过小则会导致欠拟合，因此最优的多项式阶数是关键。

二、多项式回归模型

2.1、概念

多项式回归模型是线性回归模型的一种，此时回归函数关于回归系数是线性的。多项式回归模型是一种基于多项式函数进行回归分析的模型，与多项式拟合模型类似。它也是用多项式函数来描述变量之间的关系，但不同的是它使用了最小二乘法来拟合数据，并且可以考虑多个自变量之间的关系。

多项式回归模型的一般形式可以表示为：

\[y = β_0 + β_1x_1 + β_2x_2 + ... + β_nx_n + ε \]

其中，\(y\) 表示因变量，\(x_1、x_2、...、x_n\) 是自变量，\(β_0、β_1、β_2、...、β_n\) 是多项式回归系数，\(ε\) 是误差项。

多项式回归模型可以用于非线性数据的回归分析，它的优点在于能够通过加入高次项来适应非线性数据，并且可以考虑多个自变量之间的交互作用。同时，它也存在过拟合的问题，因此需要选择合适的模型复杂度来平衡模型的拟合程度和泛化能力。

在使用多项式回归模型时，通常需要进行以下几个步骤：

• 收集数据：收集需要分析的数据，并将其按照自变量的大小进行排序。

• 选择模型：选择模型的阶数和自变量，可以通过一些方法如交叉验证、AIC、BIC 等来进行模型选择。

• 拟合数据：使用最小二乘法来拟合数据，得到多项式回归模型。

• 评估模型：通过一些指标如均方误差、确定系数等来评估拟合模型的好坏。

• 使用模型：利用拟合的模型对未知数据进行预测或者分析。

多项式回归模型在实际应用中具有广泛的应用，例如在统计学、经济学、工程学、医学等领域中常常用于建立数据与变量之间的关系，从而为决策提供依据。

2.2、实现代码

多项式回归模型示例代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

# 生成随机数据
x = np.linspace(0, 1, 10)
y = np.sin(2 * np.pi * x)

# 定义多项式回归模型
degree = 3
poly_features = PolynomialFeatures(degree=degree)
X_poly = poly_features.fit_transform(x.reshape(-1, 1))
poly_reg = LinearRegression()
poly_reg.fit(X_poly, y)
polyfit = poly_reg.predict(X_poly)

# 绘制原始数据和拟合曲线
plt.plot(x, y, 'o', label='Data')
plt.plot(x, polyfit, label='Polyfit')
plt.legend()
plt.show()

可视化：

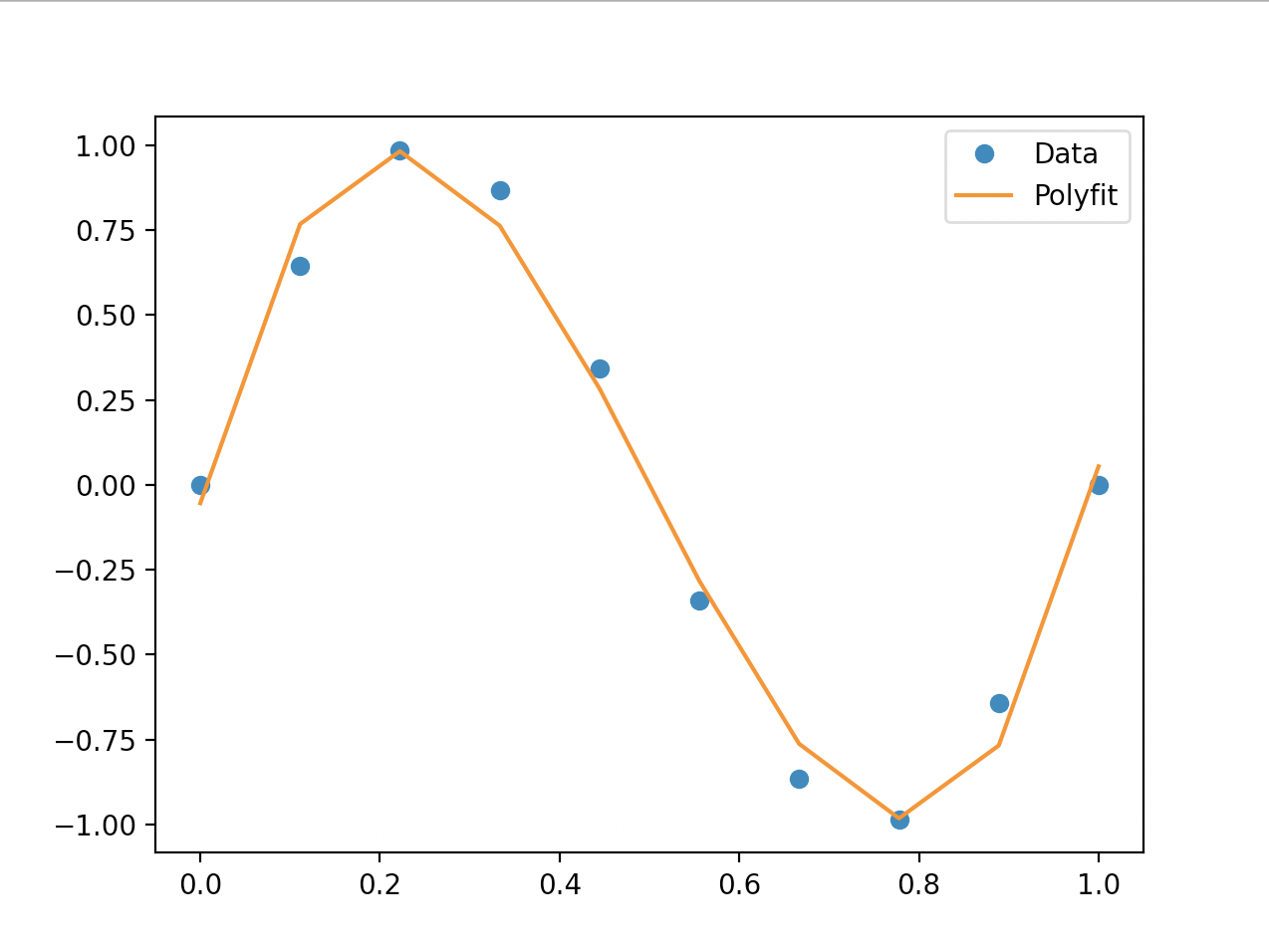
2.3、应用代码

import akshare as ak
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 获取 000001 历史行情数据
stock_hq = ak.stock_zh_a_hist(symbol='000001', adjust="qfq").iloc[:, :6]
stock_hq.columns = [
    'date', 'open', 'close', 'high', 'low', 'volume',
]
# 对获取的数据进行处理，提取出收盘价
stock_hq = stock_hq[['date', 'close']]
stock_hq['date'] = pd.to_datetime(stock_hq['date'])
stock_hq.set_index('date', inplace=True)
stock_hq = stock_hq.sort_index()


def poly_reg(degree, X_train, y_train, X_test):
    # 定义多项式回归模型
    poly_features = PolynomialFeatures(degree=degree)
    X_train_poly = poly_features.fit_transform(X_train)
    poly_model = LinearRegression()
    poly_model.fit(X_train_poly, y_train)
    X_test_poly = poly_features.fit_transform(X_test)
    y_pred = poly_model.predict(X_test_poly)
    return y_pred


# 划分训练数据集和测试数据集
n = len(stock_hq)
train_size = int(0.8 * n)
train_data = stock_hq.iloc[:train_size]
test_data = stock_hq.iloc[train_size:]

# 对用于绘图的所有数据进行处理
X = np.array(range(n)).reshape(-1, 1)
y = stock_hq.values.reshape(-1, 1)

X_train = np.array(range(train_size)).reshape(-1, 1)
y_train = train_data.values.reshape(-1, 1)
X_test = np.array(range(train_size, n)).reshape(-1, 1)
y_test = test_data.values.reshape(-1, 1)

best_degree = 0
min_rmse = float('inf')

# 交叉验证选择最优多项式阶数
for degree in range(1, 11):
    y_pred = poly_reg(degree, X_train, y_train, X_train)
    rmse = np.sqrt(np.mean((y_train - y_pred) ** 2))
    if rmse < min_rmse:
        min_rmse = rmse
        best_degree = degree

print(f"最优的多项式阶数：{best_degree}")

# 手动调整最优的多项式阶数
# best_degree = 5

# 使用最优多项式阶数进行股票预测
y_pred = poly_reg(best_degree, X_train, y_train, X_test)

# 绘图
# 原始数据
plt.plot(X, y, label='original')
# 训练数据
plt.plot(X_train, y_train, label='train')
# 测试数据（预测）
plt.plot(X_test, y_pred, label='test')
plt.legend()
plt.show()

可视化：

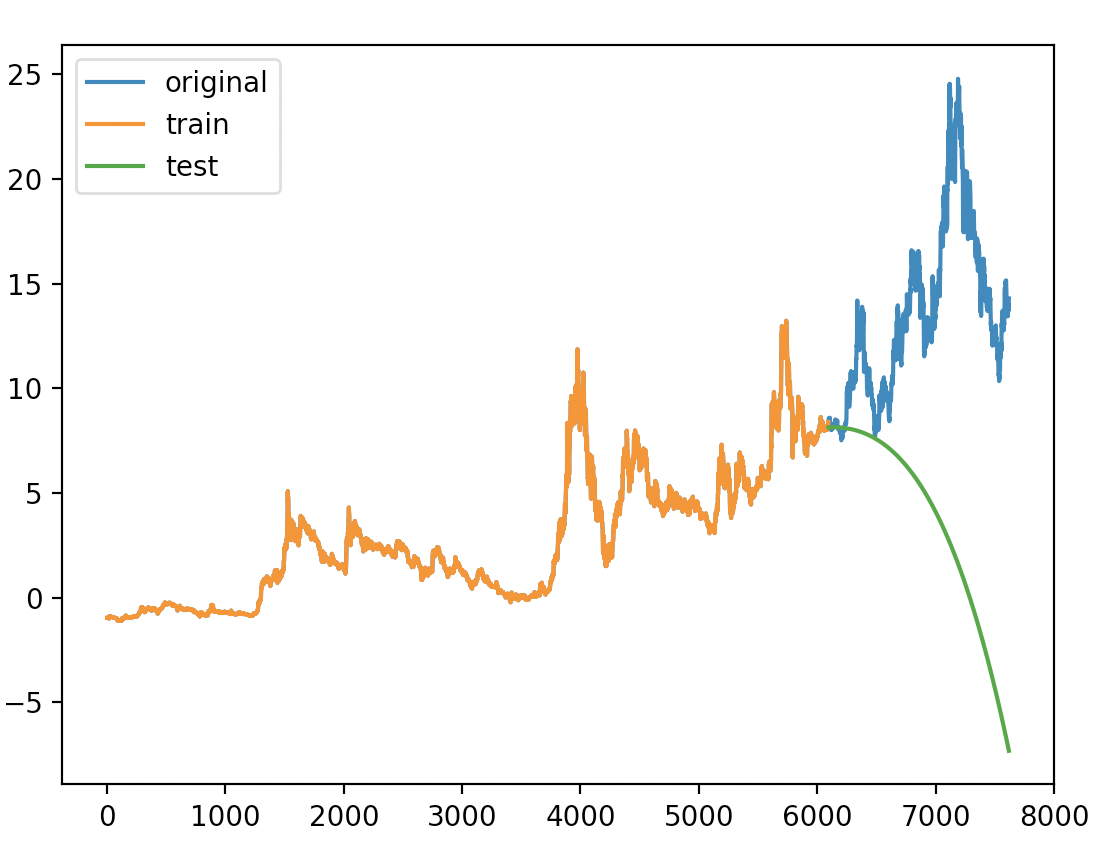
三、多项式拟合模型和多项式回归模型的区别

多项式拟合模型和多项式回归模型都是基于多项式函数进行回归分析的模型，它们的主要区别在于模型的建立方法和目的不同。

多项式拟合模型是一种通过拟合多项式方程来适应数据的模型，通常用于分析一元变量之间的关系，它的目的是在数据中找到一个适当的多项式函数来拟合数据，从而得到一个函数形式的表达式来描述变量之间的关系。

多项式回归模型是一种基于多项式函数进行回归分析的模型，它通过最小二乘法来拟合数据，可以同时考虑多个自变量之间的关系，通常用于分析多元变量之间的关系。它的目的是建立一个多元回归模型来预测因变量和自变量之间的关系，从而为决策提供依据。

因此，多项式拟合模型和多项式回归模型的应用场景和目的不同。多项式拟合模型适用于分析一元变量之间的关系，而多项式回归模型适用于分析多元变量之间的关系，通过建立多元回归模型来预测因变量和自变量之间的关系，同时可以考虑多个自变量之间的交互作用。