PWM基本原理—面积等效原理
异步电动机变频调速需要电压与频率均可调的交流电源,常用的交流可调电源是由电力电子器件构成的静止式功率变换器,一般称为变频器。回顾变频器的静止式功率变换器的控制原理。
PWM基本原理回顾
面积等效原理
采样控制理论有一个很重要的结论:“冲量相等,而形状不同的窄脉冲,加在具有惯性环节上时,其效果基本相同”[1]。
如此普适的结论,那么电力电子应该可以借助该结论找到产生期望正弦波的控制策略,看看能不能找到一些灵感,假设利用调制的脉冲群通过逆变电路能产生正弦曲线。王教授举了这样一个例子:
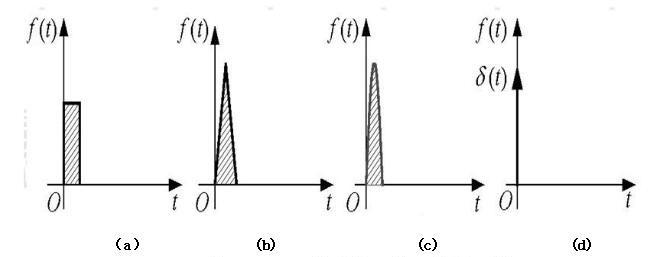
图 Fig 1.1-1a 为矩形脉冲,图 Fig 1.1-1b) 为三角形脉冲,图 Fig 1.1-2c) 为正弦半波脉冲,但它们的面积(冲量)都等于1,那么,当他们分别加载惯性的同一一个环节上时,其输出响应基本相同。当窄脉冲变成 Fig 1.1-1d 的单位脉冲函数 \delta(t) 时,其输出响应为环节的脉冲过渡函数。
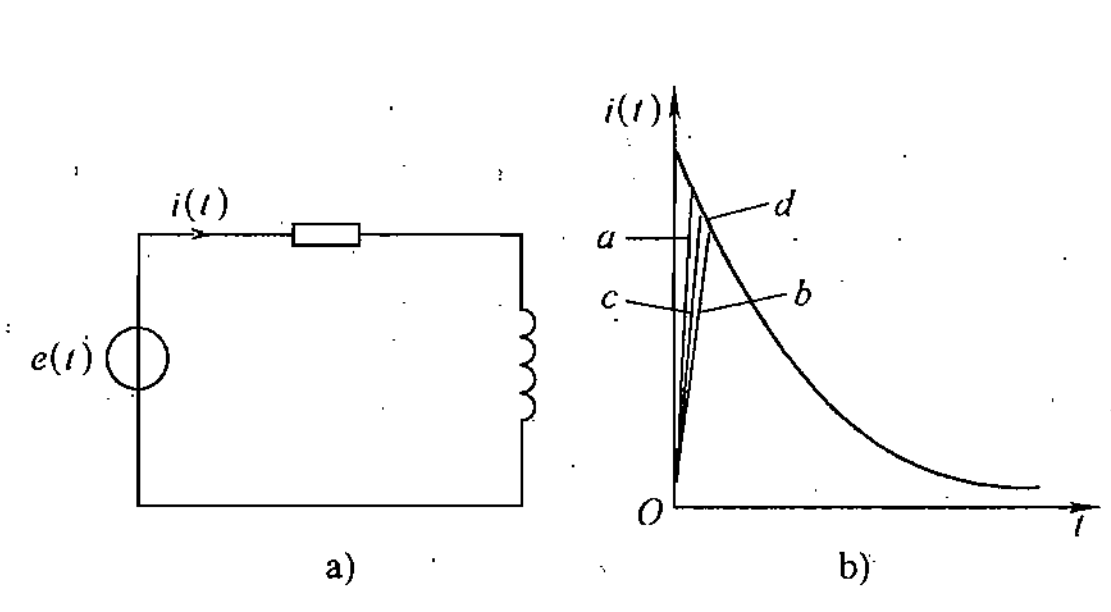
图 Fig 1.1-2 a) 中 e(t) 为电压窄脉冲,将 Fig 1.1-1 的窄脉冲a),b),c),d)作为电路的输入信号,该输入施加到具有惯性环节的 R-L 电路,设电流 i(t) 为电路输出,那么电流产生的响应波形如图 Fig 1.1-2 b) ,从波形上观察,在 i(t) 上升段,脉冲形状不同时 i(t) 的形状也略有不同,但其下降段则几乎完全相同,脉冲越窄,各i(t) 波形差异也越小。如果周期性施加 Fig 1.1-1 的窄脉冲,那么其响应i(t)也呈现周期性,这也是线性时不变系统的特征,用傅立叶级数对响应i(t)分解,可以观察到各i(t)在低频段非常接近,仅在高频段有所不同。
将图 Fig 1.1-2 a) 的电路曲线和图 Fig1.1-2 b) 响应波形特性归纳起来,那么采样控制理论结论可以很丝滑移植到在电力电子学上,在电力电子学我们则称为“面积等效原理”。
下面将介绍在面积等效原理下,通过一系列等幅,不等宽的窄脉冲来构造一个正弦半波。
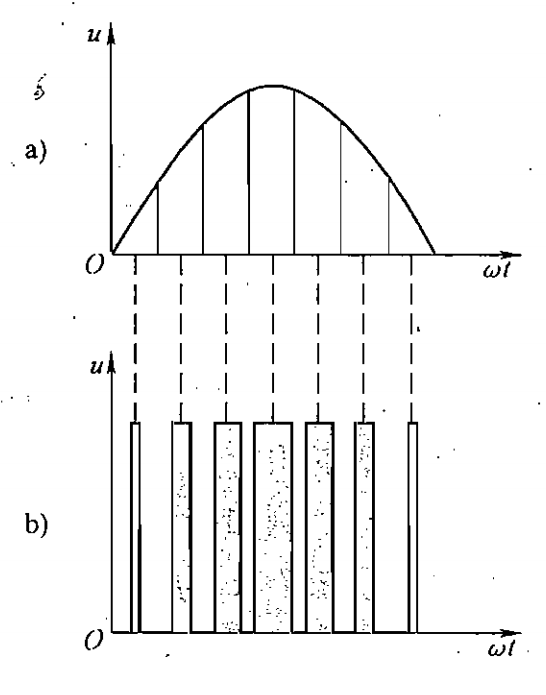
把图 Fig1.1-3 的正弦半波分成 N 等份,就可以把正弦半波看出由 N 个彼此相连的脉冲序列所形成波形,那些脉冲宽度相等,都等于 \pi/N ,但是幅值不等,且脉冲顶部不是水平直线,而是曲线,个脉冲幅值按正弦规律变化,即图 Fig1.1-3 a) ,如果把上述的脉冲序列用一系列数量等幅而不等宽的矩形脉冲代替,使矩形终点和正弦波序列对应的面积(冲量)相等,那么就得到了 Fig1.1-3b) 这样的脉冲序列.这就是PWM波形,可以看出各脉冲的幅值相等,而宽度是按照正弦规律变化的,那么根据面积等效原理,PWM波形和正弦半波是等效的,对于正弦的负半周,也可以用同样方法得到PWM波形,像这种脉冲宽度按正弦规律变化巍峨正弦等效的PWM波形,也成为SPWM波形,要改变等效输出的正弦波的幅值,只需要按照同一比例系数改变上述各脉冲宽度即可。
PWM波形可分为等幅值PWM波和不等幅值PWM波两种。有直流电源产生的PWM通常属于第一类,如直流斩波电路或者PWM逆变电路,其PWM波均是由直流电源产生,还有一种是新式的逆变电路,我们称为:“矩阵式变频电路‘,该电路很好的特点是取消了逆变电路的储能元件,由于输入电压是交流,所以矩阵式变频电路输出的是不等幅的PWM波,但不管花样千变万化,他们都是的都基于"面积等效原理"控制策略。
产生PWM波的方法的思考
如果给出逆变电路的正弦波输出频率,幅值和半个周期的脉冲数,那么PWM波形的各脉冲宽度和间隔就可以准确计算出来,按照计算结果控制逆变电路中各开关器件的通断就可以得到需要的PWM波形,这种方法称为计算法。可以看出当输出的正弦波的频率,幅值,或者相位变化时计算结果都要变化,这就很头皮发麻。
于是人们退而求其次选择调制法,将期望输出的波形作为调制信号,把接受调制的信号作为载波,通过信号波的调制得到期望的PWM波形,通常采用等腰三角波或者锯齿波作为载波,其中等腰三角波应用最为广泛,因为等腰三角波上任一点的水平宽度和高度成线性关系且左右对称,当它(等腰三角波)与任何一个平缓变化的调制信号波相交时,如果在交点时刻对电路中开关器件的通断进行控制,就可以得到宽度正比于信号波幅值的脉冲。
单相桥式逆变电路
下面将回顾单相桥式逆变电路的PWM波的产生过程来了解调制法具体的实现逻辑。
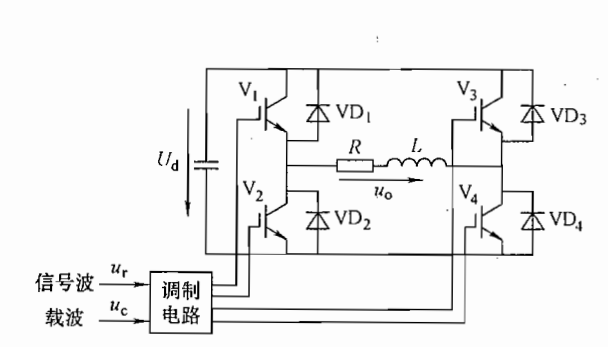
Fig 1.2-1 是采用IGBT作为开关器件的单相桥式PWM逆变电路。假设负载为阻性负载,先观察这个电路能产生什么类型电压波:
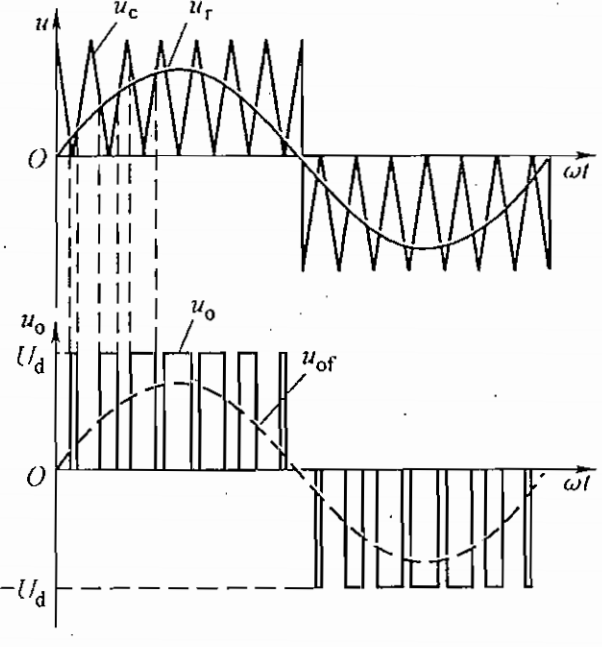
如图 Fig 1.2-2 所示,调制信号 u_\mathrm{r} 为正弦波,载波 u_\mathrm{c} 在 u_\mathrm{r} 的正半周为正极性的三角波,在 u_\mathrm{r} 的负半周为负极性的三角波,在u_\mathrm{r}和u_\mathrm{c}的交点处控制IGBT通断,其调制策略如下:
- 在 u_\mathrm{r} 的正半周, V_1 保持通态, V_2 保持断态;调制电路工作,当 u_\mathrm{r}>u_\mathrm{c} 时,使 V_4 导通, V_3 关断,使负载电压 u_\mathrm{o}=U_\mathrm{d} ;当 u_\mathrm{r}<u_\mathrm{c} 时,使 V_4 关断, V_3 导通,负载电压 u_\mathrm{o}=0 。
- 在 u_\mathrm{r} 的负半周,使 V_1 关断, V_2 导通;调制电路工作,当 u_\mathrm{r}<u_\mathrm{c} 时,使 V_4 关断, V_3 开通,负载电压 u_\mathrm{o}=-U_\mathrm{d} ,当 u_\mathrm{r}>u_\mathrm{c} 时,使 V_3 关断,V_4 导通,负载电压 u_\mathrm{o}=0 。
- 这样就可以通过SPWM波形u_\mathrm{o}来构造期望正弦波u_\mathrm{of}。
图中的虚线 u_\mathrm{of} 表示 u_\mathrm{o} 中的基波分量。像这种在 u_\mathrm{r} 的半个周期内三角波载波只在正极性或负极性一种极性范围内变化,所得到的PWM波形也只在单个极性范围变化的控制方式称为单极性PWM控制方式。
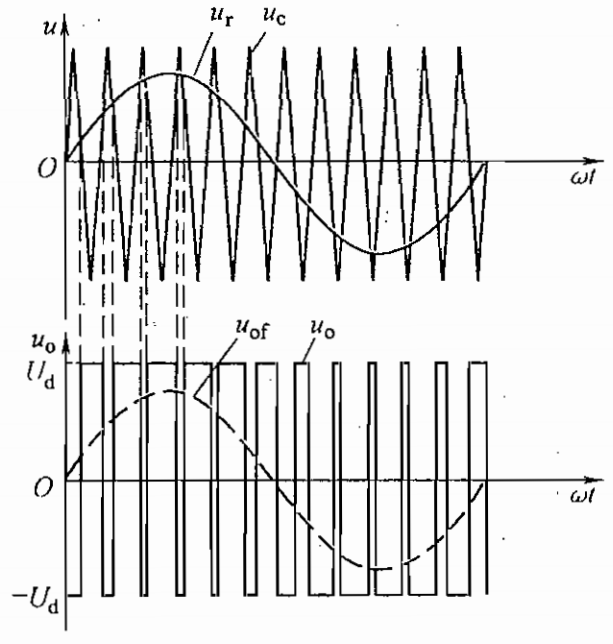
和单极性PWM控制方式相对应的是双极性控制方式。图7-4的单相桥式逆变电路在采用双极性控制方式时的波形如图7-6所示。采用双极性方式时,在 u_\mathrm{r} 的半个周期内,三角波载波不再是单极性的,而是有正有负,所得的PWM波也是有正有负。在 u_\mathrm{r}的一个周期内,输出的PWM波只有 \pm U_\mathrm{d} 两种电平。而单极性控制时还有零电平。
双极性控制控制仍然是在调制信号 u_\mathrm{r} 和载波信号 u_\mathrm{c} 的交点处控制开关管的通断,在 u_\mathrm{r} 正负半周对开关管控制规律相同,其调制策略如下:
当 u_\mathrm{r}>u_\mathrm{c} 时,给 V_1 和V_4 导通信号,关闭 V_2 和V_3 ,这时如果 i_\mathrm{o}>0 ,则V_1 和V_4 导通,如果 i_\mathrm{o}<0,则 VD_1 和 VD_4 导通,无论发生这两种情况的那一种,恒存在输出电压 u_\mathrm{o}=U_\mathrm{d} ;
当 u_\mathrm{r}<u_\mathrm{c} 时,给 V_2 和V_3 导通信号,关闭 V_1 和V_4 ,这时如果 i_\mathrm{o}<0,则控制V_2 和V_3 导通,这时如果 i_\mathrm{o}>0,则 VD_2 和 VD_3 导通,无论发生这两种情况的那一种,恒存在输出电压 u_\mathrm{o}=-U_\mathrm{d} 。
三相桥式逆变电路
研究三相逆变电路
参考
- ^王兆安,刘进军.电力电子技术[M].第五版.机械工业出版社,2009.p163



 浙公网安备 33010602011771号
浙公网安备 33010602011771号