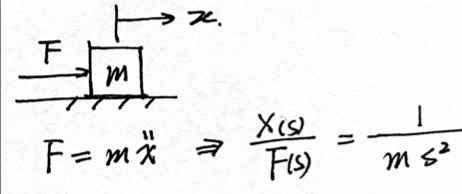为什么电压量经过PID控制器就变为电流量?电流量经过PID控制器就变为电压量?
问出这个问题的人多少具有一定的不求甚解的态度——需要一个说法——下面这个是我说服我自己的说法,拿出来和大家分享。先说结论,比例积分调节器就是一个自适应控制器。对于不知道李雅普诺夫稳定性的读者,可以不用往下看了,我也不知道该怎么从线性系统理论的角度向你们解释这件事(懒)。
【提出问题】:给定一个电流指令 i*,如何通过控制电压 u,将电机电流 i 调节至给定值——换句话说,就是将电流控制误差 i-i* 调节至零。
【数学建模】系统的模型为
读作:电压减去电阻压降等于反电势等于磁链的导数等于电感乘以电流的导数。如果是电机,可能还存在旋转反电势,如下:
读作:电压减去电阻压降等于反电势等于磁链的导数等于漏感乘以电流的导数+旋转反电势。这里应该注意到,电压可以“直接”影响电流的时间导数。同理,电压也可以“直接”影响磁链,这就是直接转矩控制(DTC)的原理。
【构造控制器】*** 已知比例积分 (PI) 调节器如下
这条式子就是你说的电流量经过 PI 变成电压。这里,假设变流器(或功率变换器,或逆变器)的传递函数为 1,即 。
【选择工具并分析】对控制器有效性的理解,一般需要借助一定的工具。 对于线性系统来说,如果已经知道了系统输入长什么样子,最直白的就是求特征根了,但是把电压输入给定 u*=u 带回系统模型中去,你会发现不知道如何去处理电流控制误差的积分项。其实,积分这件事就会导致系统状态扩张——比如在滑模控制中,可以通过引入积分项,使得初始控制误差从一开始就在滑模面上,省去趋近的过程。也就是说,你以为你面对的是一个一阶系统,但是你的 PI 控制实际上是一种“动态”控制,导致整个误差系统升阶了。当然,你可以选择令电流控制误差积分为新的状态,把它当成二阶线性系统继续分析(我不感兴趣,不作分析)。但在那之前,你不好奇为什么要用 PI 控制吗?为什么不能用 PD 控制?
为了回答这个问题,我们需要用到的分析工具是非线性系统理论中的李雅普诺夫稳定性定理。
【从无到有重新构造控制器解决所提问题】考虑下述候选李雅普诺夫函数:(候选的意思就是可能这个分析是失败的)
它沿着误差系统动态方程 的时间导数为
其中,我们假设了给定电流是常数,即 i* = Const.,其导数为零(比如,在同步旋转坐标系下)。
为了使得 负定,我们令
这不是坑爹么,电阻值 r 和旋转反电势 e2 是未知的啊。反过来说,如果 e2 为零,知道 r 的话,就可以用纯 P 对电流进行控制,如果使用的 r 值有误差,就会导致稳态控制误差。
为了解决 e2 和 r 未知的问题,这里我们构造一个自适应控制器,修改上面得到的电压表达式为:
这里的 是我们扩张的状态,用于抵消系统中未知的 ri+e2。为了得到能够达成此目的的
的表达式,我们再次使用李雅普诺夫稳定性定理,过程如下:
其中,旋转反电势的估计值 用于抵消系统中的未知部分。最后一个等式的导出,施加了如下约束:
如果该约束成立, 就是负定的,意味着电流控制误差 i - i* 会收敛至零(需要用到Barbalat's Lemma)。为了使得该约束成立,我们定义旋转反电势的估计误差为(没错,就是这么流氓)
于是,我们有
其中,注意到 是常数,所以
。总结起来,就是说,通过构造如下输入电压
就能够使得电流控制误差收敛至零。其中,这里 P 和 I 前面的负号的有无取决于控制误差的定义,如果定义为 i*-i,那就是正号。
到这里都能看懂了的话,应该就能明白为什么经过 PI 后电流误差变为电压了吧?就是因为在动态方程中,电压能够直接影响电流的时间导数(不太记得了,这种良好的性质应该是被称为相对阶为1,就是在描述系统输入和输出的相对关系)。实际上,你能解释任何使用 PI 控制器输入输出的物理量变化的原因了。比如,我们前面讨论的都是控制电感电流,如果控制对象换成一个电容,那么状态变量就是电容电压,控制输入则是电流(实际上一般还是控制的输入电压,但是输入电压减去电容电压是直接正比于输入电流的),这个时候 PI 控制器将电容电压误差变为了输入电流。
此外,你还能解释为什么 PI 控制不能调节交流给定了。在 i*(t) 是正弦波的情况下,你需要的是 Resonant control。 要是没人点赞的话我以后就少在知乎作这种严谨的回答了,可能还是抖机灵的回答更适合知乎,举个我抖机灵的例子(已经获得了九个赞了哦,厉害吧):
能不能用通俗的语言讲解一下滑模观测器SMO的原理,及其在永磁电机PMSM控制中的应用?如果你明明不懂李雅普诺夫稳定性还是看到这里了,好吧,我服你了,下面的内容姑且算是在线性系统理论里解释 PI 控制的尝试。即,我们还可以把 PI 看成阻尼和弹簧——我放一张图,可能能勾起一些人的回忆。

图中用 PI 控制机器人关节的位置误差 至零。可能已经有人意识到了,我们可以类比一下,这就算是在线性系统理论下解释 PI 的办法了。重写上面的几条式子:
接下来就是想办法得到图片中类似的式子了,把 u 的表达式代入这里的第一条式子,得:
(不好意思,之前的推导错啦)正确的误差动态是一个一阶动态方程,这里对电流控制误差的积分就是我们在前文提到了的估计项 。这里就能看出线性系统工具的局限性了:这里必须要求
为零(是否能使其为零则无从判断),电流控制误差才收敛至零;而前文的李雅普诺夫稳定性分析是能直接给出在估计误差
有界的情况下——这是李雅普诺夫函数存在的推论——就保证电流控制误差的渐近稳定性的。而且,还能够进一步证明,在满足一种名叫“持续激励”的条件的情况下,该估计误差是收敛至零的。
值得一提的是,由于我们把积分看成是一种对系统未知参数的估计, 表面上没有对误差方程求导而导致误差系统升阶,实际上则是因为我们引入了额外的状态变量 罢了。
最后再再再点题一下,由于控制是的一个感性系统(电感),输入是电压,输出是电流——这暗示着电压可以直接影响电流的时间导数——所以需要根据反馈,将电流误差经过 PI 控制变为了电压量作为系统输入。这里我们看到,为了稳定系统,根本用不到微分 (D) 控制,如果要加上微分也可以,那就相当于修改最后一条方程中一阶导数项前面的系数 ——所以它在电机暂态分析中被称为瞬态漏感(好像是)不是没有原因的。
【后记】据评论知,题主好像问得是逆变器中的双环控制,所以,我也把这边所学到那边应用了一下,也不知道对不对,传送门如下。
为什么电流电压双闭环控制器中的电流量通过PID控制器输出电压量?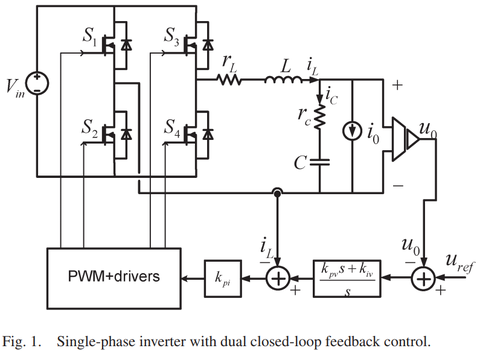
本文对微分的作用介绍很少,系统特性使然。对这部分感兴趣的可以看看这个回答:
PID 的微分环节主要作用是什么?